Шейпак А.А. Гидравлика и гидропневмопривод (часть 1)

Таким образом, получено уравнение по форме, аналогичное полученному в предыдущем параграфе, однако, в последнем случае константа сохраняет свое значение не для всей области течения, а вдоль определенной линии тока или вихревой линии. Для других линий константа может изменить свое значение. Кроме того, равенство (7.11) будет выполняться для поверхности, образованной вихревыми линиями, проходящими через определенную линию тока и наоборот. Очевидно, что

значение константы будет одинаковым для всей области течения, если векторы V и

rot V коллинеарные в каждой точке области течения.

Уравнение (7.12) для несжимаемой жидкости в равномерном поле сил тяжести, полученное как интеграл уравнений движения вдоль линии тока, также носит название уравнения Бернулли для элементарной струйки идеальной жидкости. В курсе общей физики и в некоторых курсах гидравлики оно получается с помощью общих законов сохранения массы и энергии.

Уравнение (7.12) можно записать в трех формах:

причем слагаемые в этих уравнениях можно трактовать как составляющие удельной энергии жидкости, отнесенные к единице веса, массы и объема, соответственно.

Введем следующую терминологию для слагаемых в системе (7.13): H – полный напор;

z – геометрический напор; ρpg – пьезометрический напор;

V 2 – скоростной напор (динамический напор);

2g

z + ρpg – гидростатический напор;

gH – полная удельная механическая энергия движущейся жидкости; gz – удельная энергия положения;

ρp – удельная энергия давления движущейся жидкости;

V 2 – удельная кинетическая энергия;

2

gz + ρp – удельная потенциальная энергия;

p–гидростатическое давление;

ρV 2 – динамическое давление.

2

61

7.3.3.Неустановившееся потенциальное движение

Врассмотриваемом случае rot V = 0 или V = grad ϕ .

Скалярная функция ϕ является функцией координат и времени, причем последнее рассматривается как параметр.

Так как порядок операций ∂∂t и grad можно поменять, уравнение движения

для баротропной жидкости в поле массовых сил, имеющих потенциал, примет следующий вид:

grad ∂ϕ ∂t + Φ +P + V22 = 0.

Следовательно, можно записать, что

где f(t) – произвольная функция времени.

Равенство (7.14) носит название интеграла Коши-Лагранжа.

Для несжимаемой жидкости в равномерном поле сил тяжести из (7.14) получаем уравнение

Рассмотрим в некоторый момент времени произвольную трубку тока (рис. 7). Так как правая часть уравнения (7.15) зависит только от времени, то для двух сечений трубки можно записать следующее равенство:

Если l – криволинейная координата, отсчитываемая вдоль трубки тока, то

С учетом проделанных выкладок уравнение (7.16) можно переписать следующим образом:

Равенство (7.17) носит название уравнения Бернулли для неустановившегося движения струйки идеальной жидкости.

Запишем уравнение расхода в следующем виде:

62

быть легко вычислена из геометрических соотношений).

Уравнение Бернулли для неустановившегося движения струйки идеальной жидкости может быть записано теперь следующим образом:

7.3.4.Интегралы уравнений движения для баротропного газа

Вслучае рассмотрения движения газа можно пренебречь влиянием массовых сил. Функция давления P принимает различный вид в зависимости от процессов изменения параметров состояния. Рассмотрим изотермическое течение термически совершенного газа. В этом случае:

Интеграл Бернулли при условии пренебрежения массовыми силами можно записать следующим образом:

В случае адиабатного (изоэнтропного) течения газа уравнение процесса будет

где k – показатель адиабаты.

Функция давления в этом случае будет

Уравнение Бернулли для адиабатного движения идеального термически совершенного газа примет следующий вид:

Если V0 <<V , то можно получить зависимость

называемую формулой Сен-Венана-Вантцеля.

Уравнения (7.21), (7.22) и (7.23) целесообразно использовать лишь при существенной сжимаемости газа, что имеет место при скоростях, приближающихся к

63

скорости звука. При движении газа с малыми скоростями (для воздуха при нормальных температурах до 100 м/c) можно пользоваться уравнением Бернулли для несжимаемой жидкости. При этом хорошие результаты дает применение в расчетах среднего значения плотности.

7.4. Гидродинамический парадокс Эйлера—Д’аламбера

Одним из простейших примеров потенциальных течений является установившееся обтекание потоком несжимаемой невязкой жидкости сферы радиуса R с центром в начале координат. Предположим, что скорость невозмущенного потока параллельна оси и имеет величину V. Решение получается наложением течения, вызванного диполем, на однородный поток. В результате легко вычислить теоретическое распределение давлений вокруг сферы для течения. Если не учитывать гидростатические силы, то оказывается, что распределение давлений впереди и позади сферы вполне симметрично и, следовательно, результирующая сила давления равна нулю. Аналогичный результат можно получить и для нулевой подъемной силы, что находятся в явном противоречии с каждодневным опытом.

Это теоретическое заключение, называемое парадоксом Эйлера-Даламбера, относится не только к сфере; его можно распространить и на тела произвольной формы.Отсюда следует теорема [4]:

Теорема 1. Система гидродинамических сил, действующих на какое-либо тело конечных размеров в бесконечном установившемся потоке, удовлетворяющем условиям потенциального течения, эквивалентна нулю или паре сил.

Понятие потенциального течения, основанное на гипотезе «идеальной жидкости», неявно использует два независимых топологических предположения: линии тока сплошь заполняют все пространство вне тела; локально однозначный потенциал скорости однозначно определен во всем пространстве. В то же время не существует никаких математических доводов против корректности течений Н.Е.Жуковского с циркуляцией, течений со следом и многих других топологических типов течений. Очевидно, можно сделать заключение о неполноте теории невязкой жидкости. Рассуждения, приводящие к понятию установившегося течения жидкости, неубедительны. Теория идеальной жидкости с большим успехом применяется для расчета неустановившихся течений. Потенциальные течения жидкости, математически возможны, но они могут быть неустойчивыми. Вероятно, что беспорядочные вихревые движения в следе, теоретически вводимые при изучении течения идеальной жидкости, мало отличающегося от потенциального течения (например, течения Кармана с бесконечными вихревыми дорожками), являются удовлетворительной математической моделью процессов, наблюдаемых при больших числах Рейнольдса. Следует считать, что задачи с симметричными условиями могут и не иметь устойчивых симметричных решений. Таким образом, парадоксы теории идеальной жидкости могут являться парадоксами топологического переупрощения и парадоксами симметрии [4].

Отметим, что рассмотрение парадокса Даламбера приводит к известному инженерному решению: путем «отсасывания пограничного слоя» в жидкости достаточно малой вязкости сопротивление можно свести к очень малой величине. Описанная операция требует относительно небольшого расхода энергии.

64

8. ОБЩЕЕ УРАВНЕНИЕ ЭНЕРГИИ В ИНТЕГРАЛЬНОЙ И ДИФФЕРЕНЦИАЛЬНОЙ ФОРМАХ

Применим первое начало термодинамики для контрольного объема, являющегося незамкнутой системой. Уравнение энергии примет тогда следующий вид:

Знак ∑ означает суммирование всех протекающих и вытекающих потоков;

q − все виды переноса тепла на границе контрольного объема: E − все виды энергии, накопленной в контрольном объеме; hF = e + pv , где e = E на единицу массы потока; w − массовая скорость; Wx − вся выполненная механическая работа, за ис-

ключением обратимой работы потока.

Таким образом, поток тепла в систему и поток энергии, входящей с массой, включая обратимую работу потока равны сумме потока внутренней энергии, потока энергии, который покидает систему вместе с массой, включая обратимую работу потока, и потока полезной работы, за исключением обратимой работы потока. В тепловой член можно включить все виды передачи тепла: радиацию, конвекцию и теплопроводность. В работу при необходимости можно включить все взаимодействия с окружающей средой, не входящие в члены переноса тепла и массы. Можно учесть не только механические эффекты, но и взаимодействия полей, например, электромагнитного. В члены переноса массы должны быть включены все виды энергии, связанные с переходом массы через границы нашей системы, в том числе энергия, связанная с химическими превращениями, если таковые имеют место. В определенном смысле конкретная запись общего уравнения энергии может явиться выражением наших современных знаний, если только последние не являются менее полными, чем мы считаем на самом деле.

Уравнение энергии в дифференциальной форме запишем в общем виде для сжимаемой сплошной среды. Рассматривая движение элементарного объема dxdydz при его движении вместе с остальной жидкостью, в соответствии с первым началом термодинамики, подводимое к этому объему тепло расходуется на увеличение полной энергии и на выполнение работы:

Все входящие в это уравнение производные являются субстанциональными, имеющими в общем случае локальные и конвективные составляющие.

Учитывая подвод тепла только за счет теплопроводности, согласно закону Фурье, после ряда преобразований, можно получить уравнение энергии для термически совершенного газа в следующем виде:

65

Функция Ф, называемая диссипативной, равна:

В общем случае cp − удельная теплоемкость при постоянном давлении, λ −

коэффициент теплопроводности, зависят от температуры (для термически несовершенного газа и от давления). При постоянном коэффициенте теплопроводности уравнение энергии в дифференциальной форме упрощается и принимает следующий вид:

Для несжимаемой жидкости уравнение при постоянном коэффициенте теплопроводности принимает более простой вид:

66

9. ОБЩАЯ ИНТЕГРАЛЬНАЯ ФОРМА УРАВНЕНИЙ КОЛИЧЕСТВА ДВИЖЕНИЯ И МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ

9.1. Основные сведения

Запишем уравнение второго закона Ньютона в форме закона сохранения импульса или количества движения. Отметим, что в отечественной литературе по общей физике чаще используется термин «импульс», а в курсах теоретической механики – «количество движения», в английском языке – “momentum”.

где Vi − скорость в любой произвольно выбранной инерциальной системе координат; VR − относительная скорость на граничной поверхности контрольного объема; ρ − плотность; t − время; σ − напряжение; A − площадь; V − объем.

Уравнение (9.1) легко приводится к более удобной форме, когда Vi =VR . В

этом случае контрольный объем не ускоряется, а координаты связаны с контрольной поверхностью.

Записанное уравнение применимо к любой макроскопической контрольной поверхности при отсутствии релятивистских эффектов.

9.2.Применение закона импульса и закона момента импульса

вмеханике жидкости

Эти законы установлены в механике для любой системы материальных точек, между которыми действуют силы взаимодействия, попарно равные и противоположно направленные, вследствие чего главный вектор и главный момент внутренних сил равны нулю в любой момент движения. Оба этих закона справедливы как для идеальной, так и для вязкой жидкости.

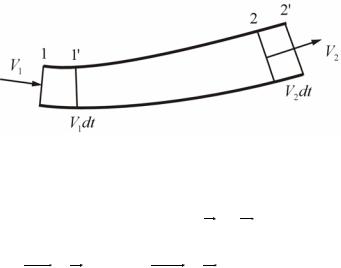
Рис. 21. Применение законов сохранения импульса и момента импульса в механике жидкости и газа

Рассмотрим установившееся движение жидкости в элементарной трубке тока (рис. 21). Пусть скорости в сечениях 1 и 2 будут V1 и V2 , соответственно, и за время dt жидкий объем из положения 1-2 перейдет в положение 1’-2’, так, что

67

Так как движение установившееся, то объемы 1’-2 будут иметь один и тот же импульс в момент времени t и t + dt.

В соответствии с уравнением расхода

dm =V1dtρ1dA1 =V2dtρ2dA2.

Таким образом, изменение импульса за время dt будет:

dK =V2 dm −V1dm .

Это изменение импульса равно элементарному импульсу всех внешних сил (массовых и поверхностных), приложенных как к боковой поверхности трубки, так и к сечениям 1 и 2. Если массовыми силами можно пренебречь, то остаются только поверхностные силы (в случае идеальной жидкости – только силы давления).

dK =V2 dm −V1dm = Pdt

или

1 и 2, L – главный момент внешних сил, приложенных ко всей замкнутой поверхности объема (1 + 2 ) .

Полученные равенства могут быть объединены теоремой Эйлера: сумма всех внешних сил, приложенных ко всей поверхности произвольного объема трубки тока, эквивалентна в случае установившегося движения двум силам

приложенным к конечному и начальному сечениям и численно равным секундным импульсам жидкости, вытекающей и втекающей в трубу.

Рис. 22. Внезапное расширение потока с неравномерной (ступенчатой) эпюрой скоростей на входе

68

Применим полученный результат к течению жидкости со ступенчатой эпюрой скоростей во входном сечении и с равномерной эпюрой в выходном сечении после внезапного изменения площади сечения (рис. 22). Будем пренебрегать потерями на трение между сечениями 1 и 2, а давление в сечении 1"а" будем считать равным давлению в сечении 1 (последнее утверждение подтверждается экспериментально для случая турбулентного режима течения).

Тогда уравнение импульса можно записать в следующем виде:

(p1 − p2 )A2 = ρV11 A11 (V2 −V11 )+ ρV12 A12 (V2 −V12 ).

Уравнение Бернулли, с учетом неравномерности распределения скоростей в первом сечении, будет

где h – гидравлические потери (местные) на участке 11-22.

Заметим, что выравнивание потока, как показывает эксперимент, происходит на длине l, равной примерно трем разностям диаметров труб: l = 3 (D – d).

Уравнение расхода запишем в следующем виде:

V11 A11 +V12 A12 =V2 A2 .

Будем считать известными следующие величины: V11, V12, A11, A12, A2. Тогда

Величины ( p2 − p1 ) и h легко найти после простых алгебраических преобразо-

Из анализа полученных зависимостей можно сделать важное заключение о том, что гидравлические потери в местных сопротивлениях существенно зависят от неравномерности эпюры скоростей на входе в канал. Так, если принять, что

A11 = A12 и A2 >> A1 , то

В то же время потери, подсчитанные по средней скорости, должны составить:

2gh = (V11 +V12 )2 .

4

69

Вводя обозначение V12 = V11 (1 + x), можно получить: hh =1+ 34x2 .

Таким образом, потери в предельном случае x = 1 будут на 75% больше, чем

при равномерной эпюре скоростей.

Законы импульса и момента импульса часто применяются для расчета силы воздействия установившегося потока жидкости на твердое тело, помещенное в него полностью или частично.

9.3. Определение силы, действующей на стенки диффузора и конфузора

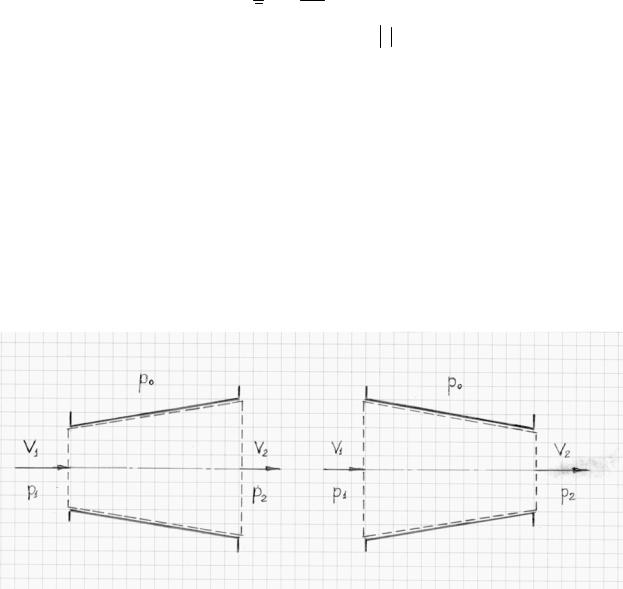
На рис. 23 приведены схемы диффузора и конфузора (дозвукового сопла). Давление внутри по длине канала переменно, снаружи на боковую стенку действуют силы атмосферного давления, которое в избыточной системе измерения давления равно нулю. Поперечные составляющие, перпендикулярные оси канала, взаимно уравновешиваются, воспринимаясь материалом стенки. Продольные составляющие образуют силу, которая воспринимается узлами крепления канала.

Рис. 23. Схемы диффузора и конфузора

Контрольная поверхность состоит из трех участков: входное сечение, выходное сечение и участок, вплотную примыкающий к боковой стенке. В проекции на ось x уравнение импульса запишется как

Обозначив силу действия потока на стенки канала F , запишем:

p1 A1 − p2 A2 − F = ρV1 A1 (V2 −V1 ).

Сила, действующая на боковую стенку, будет равна:

F = p1 A1 − p2 A2 + ρV1 A1 (V1 −V2 ).

70