
Шейпак А.А. Гидравлика и гидропневмопривод (часть 1)
.pdf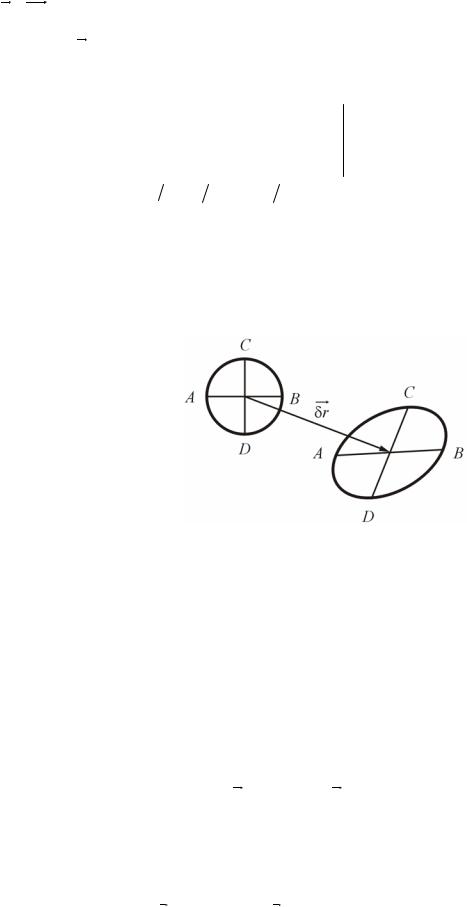
ω ×δr |
|
– скорость вращательного движения вокруг мгновенной оси с угловой |
|
|
|
|
|
|
скоростью ω ;
grad F – скорость чистой деформации.
Формула (3.12) использует понятие тензора скоростей деформаций
|
S&11 |
S&12 |
S&13 |
|
|||
S& = |
S&21 |
S&22 |
S&23 |
|
S&31 |
S&32 |
S&33 |
с компонентами S&ij =1 2 (∂Vi ∂x j + ∂V j ∂xi ), где xi и xj принимают в декартовой сис-
теме координат значения x, y, z.
Диагональные составляющие тензора скоростей деформации характеризуют скорости относительного изменения длины отрезка, а их сумма – скорость изменения относительного объема элементарной частицы жидкости. Компоненты S&ij при
i ≠ j характеризуют скорость угловых деформаций или деформаций сдвига.
Рис. 9. Движение жидкой частицы
На рис. 9 показано плоское движение жидкой частицы жидкости: поступательное, вращательное (поворот отрезков АВ и СD) и деформационное (изменение длин отрезков АВ и СD и изменение величины угла между отрезками АВ и СD).
Соотношение (3.12) имеет важное практическое значение. Одним из современных методов измерения локальных скоростей является наблюдение за твердыми частицами с плотностью, равной плотности жидкости. Очевидно, что при таком методе пропадает деформационная составляющая скорости в масштабе размера вводимой твердой частицы. При наблюдении за жидкими частицами этой систематической ошибки метода измерения не будет.
Рассмотрим теорему Гельмгольца о вихрях. Введем понятие потока вектора вихря:
∫rotn VdA = ∫div rot VdW.
A W
Очевидно, что поток вектора вихря скорости через боковую поверхность вихревой трубки равен нулю (по определению). Из векторного анализа известно, что поток любого вектора через любую замкнутую поверхность, внутри которой нет особенностей, равен нулю. Рис. 7 можно рассматривать и в качестве вихревой труб-
ки с заменой вектора V вектором rot V . Проводя рассуждения, аналогичные приведенным в разделе 3.3, легко получить, что
31

∫rot−n VdA = |
∫rotn VdA |
(3.13) |
A1 |
A1 |
|
или |
|
|
∫ω−n dA = |
∫ωn dA. |
(3.13а) |
A1 |
A1 |
|
Равенство (3.13) выражает теорему Гельмгольца о вихрях: поток вихря скорости через поперечное сечение трубки в данный момент времени постоянен по ее длине. Если вихревая трубка является элементарной, то в пределах каждого из сечений будет ω = c o n s t и, следовательно,
ω1 A1 = ω2 A2 |
èëè ω = const |
(3.14) |
Из теоремы Гельмгольца вытекают важные для практических приложений следствия.
1.Сечение вихревой трубки не может стать равным нулю, так как для этого требуется физически невозможное бесконечно большое значение угловой скорости.
2.Вихревые трубки не могут заканчиваться внутри жидкости. Они либо образуют вихревые кольца, замыкаясь на себя, либо «опираются» на стенку, ограничивающую поток, или на свободную поверхность.
Теорема Стокса устанавливает зависимость между циркуляцией и потоком вихря скорости: поток вектора вихря скорости через любую поверхность, опирающуюся на некоторый замкнутый контур, равен циркуляции скорости по этому контуру:
Γ = ∫rotn VdA = ∫V dl. |
(3.15) |
|
A |
L |
|
Циркуляция скорости по замкнутому контуру может служить, наряду с потоком вихря, мерой интенсивности вихревого движения, и это понятие широко применяется в теоретических построениях и на практике, например, при проверке качества изготовления впускных коллекторов двигателей внутреннего сгорания.
Отметим, однако, что локальная характеристика rotn V точнее описывает картину
течения, чем интегральные Γ или ∫rot VdA.
A
3.5. Плоские потоки несжимаемой жидкости. Функция тока
Плоские потоки жидкости, когда, например, Vz = 0, являются очень важными видами течения, легко представляемыми графически. Существует мнение, что развитие расчетных методов для пространственных потоков сдерживается не только быстродействием и памятью ЭВМ, но и трудностью представления трехмерных течений.
Уравнение неразрывности для плоского потока несжимаемой жидкости будет
∂V |
x |
+ |
∂Vy |
= 0 |
или |
∂V |
x |
= − |
∂Vy |
. |
|
|
∂y |
∂x |
∂y |
||||||
∂x |
|
|
|
|
||||||
Очевидно, что выражение Vx dy −Vy dx является полным дифференциалом неко-
торой функции ψ :
dψ = ∂∂ψx dx + ∂∂ψy dy = Vx dy −Vy dx.
32

Сравнивая коэффициенты при dx и dy, находим:
|
Vx = |
∂ψ |
è |
Vy = − |
∂ψ |
. |
(3.16) |
|||
∂y |
|
|||||||||
|
|
|
|
|
|
|
∂x |
|
||
Уравнения линий тока для плоского потока будут |
|
|||||||||
|
dx |
= |
dy |
, |
или |
Vx dy −Vy dx = 0. |
|
|||
|
Vx |
|
|
|||||||
|
Vy |
|
|
|
|
|
||||
Таким образом, вдоль любой линии тока будет dψ = 0, или ψ = c o n s t . Следо-
вательно, функция тока имеет свойство сохранять вдоль любой линии тока постоянное значение, которое, однако, зависит от линий тока.
Существование линий тока не зависит от наличия или отсутствия в жидкости вихрей. Однако оно вытекает из уравнения непрерывности для плоских течений, и поэтому функция тока существует только для плоских течений. Особенно просто рассчитывается поле течения, если поток не только плоский, но и потенциальный,
т.е. скорость является градиентом некоторой скалярной функции ϕ: |
|
|||
|
V = grad ϕ. |
(3.17) |
||
В этом случае во всем потоке rot V |
= 0, т.е. течение является безвихревым. |
|||
Для безвихревого (потенциального) течения жидкости из уравнения неразрыв- |
||||
ности следует: |
|
|
|
|
∂2ϕ |
+ |
∂2ϕ |
= 0 |
|
∂x 2 |
∂y2 |
(3.18) |
||
|
|
и |
|
|
∂2ψ2 |
+ |
∂2ψ2 |
= 0 |
(3.19) |
∂x |
|
∂y |
|
|
Таким образом, задача нахождения поля скоростей сводится к решению уравнения Лапласа. Отметим, что в общем случае потенциал и функция тока могут быть функциями координат и времени, причем время в уравнениях (3.18) и (3.19) является не аргументом, а параметром.
Для вихревого движения уравнение (3.19) заменяется уравнением Пуассона:
|
2 |
ψ2 |
|
2 |
|
∂Vx |
|
∂Vy |
→ |
|
∂ |
|
+ |
∂ ψ2 |
= |
− |
= −rot z V . |
(3.20) |
|||
∂x |
|
∂y |
|
∂y |
|
∂x |
|
|
||
Численные методы решения уравнений (3.19) и (3.20) аналогичны.
33
4.СИЛЫ, ДЕЙСТВУЮЩИЕ В ЖИДКОСТЯХ
4.1.Напряжения поверхностных сил
Напряженное состояние жидкости обусловлено массовыми и поверхностными силами (см. раздел 2).
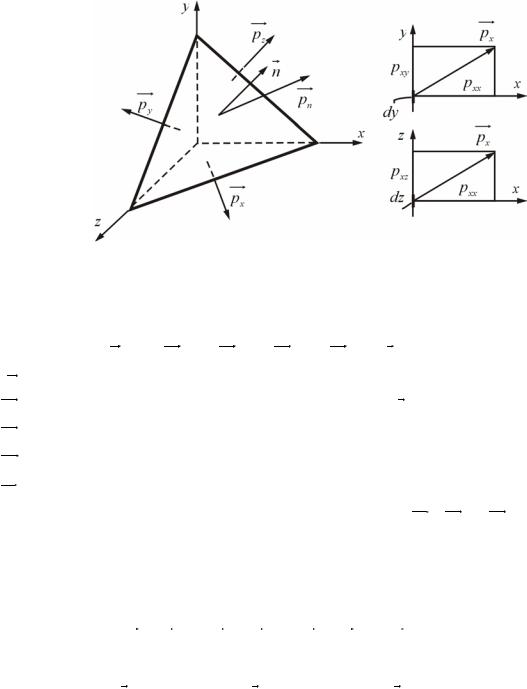
Рис. 10.Напряженное состояние жидкости
Рассмотрим жидкую движущуюся частицу в виде тетраэдра с вершиной в начале координат (рис. 10). Применяя к этому жидкому объему второй закон Ньютона, получим:
Fρδw + pnδAn − pxδAx − pyδAy − pzδAz = aρδw,
где F – единичная массовая сила;
pn – напряжение на грани, нормальной направлению n ; px – напряжение на грани, нормальной оси X;
py – напряжение на грани, нормальной оси Y; pz – напряжение на грани, нормальной оси Z.
Знак “ – “ перед слагаемыми, содержащими напряжения px , py и pz , обусловлен
тем, что положительные направления напряжений и координатных осей X, Y и Z противоположны.
Разделив исходное уравнение на δAn и принимая во внимание, что δw = (1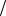 3)hδAn , при переходе к пределу получим:
3)hδAn , при переходе к пределу получим:
pn = px cos(x, n) + py cos(y, n) + pz cos(z, n), |
(4.1) |
|||||||
где |
δA |
|
|
δAy |
|
|
δA |
|
cos(x, n) = |
|
cos(y, n) = |
|
cos(z, n) = |
||||
x |
, |
|
, |
z . |
||||
δA |
δA |
|||||||
|
|
|
|
|
δA |
|||
|
n |
|
|
n |
|
|
n |
|
Спроектируем векторное равенство (4.1) на координатные оси X, Y и Z.
34

pnx = pxx cos(x,n) + pyx cos( y,n) + pzx cos(z,n), |
|
pny = pxy cos(x,n) + pyy cos( y,n) + pzy cos(z,n), |
(4.2) |
pnz = pxz cos(x,n) + pyz cos( y,n) + pzz cos(z,n).
Для каждой из проекций используются два индекса: первый определяет ориентацию площади (направление нормали), а второй – координатную ось, на которую проектируется соответствующий вектор. Очевидно, что pxx , pyy и pzz суть нор-
мальные напряжения, а проекции с разноименными индексами – касательные напряжения (см., например, для px на рис. 10 справа).
Записав уравнение моментов, можно доказать теорему о взаимности касательных напряжений:
pxy = pyx , |
pxz = pzx , |
pyz = pzy . |
(4.3) |
Шесть независимых скалярных величин, определяющих напряженное состояние жидкости, образуют симметричный тензор напряжений:
|
pxx |
pyx |
pzx |
|
|
Π = |
pxy |
pyy |
pzy |
. |
(4.4) |
|
pxz |
pyz |
pzy |
|
|
Предположим, что все касательные напряжения равны нулю. Это может иметь место в двух случаях: либо если жидкость находится в покое, либо в случае модели идеальной жидкости. Тогда из (4.3) следует
pnx = pxx cos(x, n), pny = pyy cos(y, n), pnz = pzz cos(z, n).
Величины pnx , pny и pnz |
можно вычислить и из следующих равенств: |
|
pnx = pn cos(x, n), |
pny = pn cos(y, n), |
pny = pn cos(z, n). |
Сопоставляя две серии равенств, получим: |
|
|
pn = pxx = pyy = pzz = −p, |
(4.5) |
|
где p – гидродинамическое давление в идеальной жидкости или гидростатическое давление в покоящейся реальной жидкости. Эта величина положительна, так как жидкая среда, как отмечалось ранее, не выдерживает растягивающих напряжений. Давление p отождествляют с термодинамическим давлением, входящим в термическое уравнение состояния. Утверждение о независимости величины давления в покоящейся жидкости от ориентации элементарной площадки называется законом Паскаля.
Совокупность значений давления во всех точках жидкости в данный момент времени образует поле давления p( r ,t).
4.2.Давление абсолютное, избыточное, вакуумметрическое
Втермическое уравнение состояния, как и в большинстве аналитических выражений, описывающих физические законы, входит абсолютное давление, обусловленное молекулярно-кинетической теорией. Существуют приборы, позволяющие измерить величину этого давления, однако, устройство их достаточно сложное, а стоимость высокая. На практике проще организовать измерение не абсолютной величины давления, а разности двух давлений: искомого и атмосферного (барометрического). Знание величины атмосферного давления, измеренного с помо-
35
щью того или иного типа барометра, позволяет легко получить и величину абсолютного давления. Часто достаточную точность обеспечивает знание средней величины атмосферного давления. Если определяемая величина давления больше атмосферного, то положительная величина разности давлений называется избыточным давлением, которое измеряется различными типами манометров. Если определяемая величина давления меньше атмосферного, то избыточное давление является отрицательной величиной. Абсолютное значение разности давлений называется в этом случае вакуумметрическим давлением; оно может быть измерено посредством вакуумметров различного типа.
Если измеряемое давление больше атмосферного, то pабс = ризб. + pатм.; если
измеряемое давление меньше атмосферного, то pабс. = pатм. – pвак и pвак = - ризб. Размерность давления [p] = ML -1T –2. Единица давления в Международной
системе единиц называется паскаль (Па). Паскаль равен давлению, вызываемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м2: 1 Па = 1 Нм -2 = 1 кг м-1 с-2. В США, Великобритании и некоторых других странах на практике давление часто измеряют в фунтах на квадратный дюйм
(lb/sq.inch или psi). 1 бар = 105 Па ≈ 14,5 фунт/кв. дюйм.
Длинная (около 1 м), запаянная с одного конца трубка, заполненная ртутью и опущенная открытым концом в сосуд со ртутью, сообщающийся с атмосферой, называется ртутным барометром. Он позволяет определять давление атмосферы по высоте столбика ртути, заполняющего трубку. Прибор впервые описан Е.Торричелли (Е. Torricelli) в 1644 г. Проведение систематических количественных измерений давления атмосферы с помощью ртутного барометра предложено Декартом в 1647 г. Действие прибора основано на том, что давление в области над поверхностью ртути в трубке пренебрежимо мало (объем пространства над ртутью в трубке называется торричеллиевой пустотой). В этом случае из условий механического равновесия ртути следует связь между давлением атмосферы и высотой столба ртути: p0 = ρgh. Давление паров ртути в торричеллиевой пустоте при температуре T = 273 К составляет 0,025Па.
Давление атмосферы (или атмосферное давление) зависит от высоты места наблюдения и погодных условий. В обычных условиях на уровне моря высота столба ртути составляет около 76 см и уменьшается при подъеме барометра.
В геофизике принята модель стандартной атмосферы, в которой уровню моря соответствуют температура Т =288.15 К (150С) и давление p0 =101325,0 Па. Состояние газа с таким же давлением при температуре Т = 273.15 К (00C называется нормальными условиями. Близкие к величине атмосферного давления значения pT = 9.81 104 Па, рB =105 Па и pF =1.013.105 Па используются в естествознании и технике для измерения давлений и называются технической атмосферой (pT), ба-
ром (рB) и физической атмосферой (pF).
При постоянной температуре атмосферы изменение давления с высотой h описывается барометрической формулой, учитывающей сжимаемость воздуха:
p = p0 e -µgh/RT
Здесь µ − молярная масса воздуха µ = 29 10-3 кг моль -1, g − ускорение свободного падения вблизи поверхности Земли, Т − абсолютная температура, a R − молярная газовая постоянная R =8.31 Дж К-1моль-1.
36
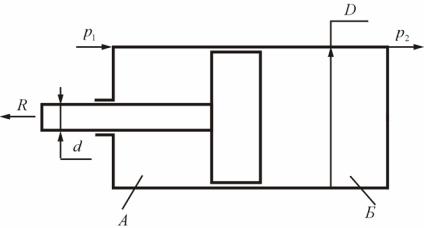
4.3. Несколько задач
Определить силу R , которую надо приложить к штоку для движения поршня с постоянной скоростью. Трением пренебречь. D = 20ìì , d =10ìì .
= 750ìì ðò . ñò (mm Hg).
4.3.1.p1 = 2 áàð èçá. p2 = 6 áàð èçá.
4.3.2.p1 = 0,5 áàð âàê. p2 = 5,5 áàð èçá
4.3.3.p1 = 80 psi èçá p2 =10 psi èçá
4.3.4. p |
= 6 105 Ïà èçá |
1 |
|
p2 |
= 30 psi èçá. |
4.3.5.p1 =10 psi âàê.
p2 = 4 êãñ/ ñì 2 èçá.
4.3.6. p = 6 105 |
Ïà àáñ. |
1 |
|
p2 =1,5 êãñ/ ñì 2 èçá.
4.3.7.p1 = 0,4 êãñ/ ñì 2 âàê. p2 = 0,8 êãñ/ ñì 2 âàê
37

5. ОБЩИЕ ЗАКОНЫ И УРАВНЕНИЯ СТАТИКИ И ДИНАМИКИ ЖИДКОСТЕЙ И ГАЗОВ
5.1. Уравнение движения жидкости в напряжениях
y 
px |
px + |
px |
dx |
x |
x
z 
Рис. 11. К выводу уравнения движения жидкости в напряжениях
Рассмотрим движение жидкого параллелепипеда со сторонами dx, dy, dz. На жидкую частицу действует массовая сила ρFdxdydz и поверхностная сила на шесть граней. Рассмотрим сначала грани, нормальные оси X (рис. 11). На левую грань
действует поверхностная сила |
px dydz , на правую грань – |
|
∂ px |
|
|
|
|||
px + |
|
∂x dx dydz . От- |
||
|
|
|
|
|
→
метим, что p x является векторной величиной и при изменении координаты меняется как по величине, так и по направлению. Суммарная сила на две грани будет
∂px ∂x dxdydz . Аналогичные рассуждения для других осей дадут еще две состав-
ляющие поверхностных сил ∂ py ∂x dxdydz и ∂pz ∂x dxdydz . Тогда уравнение движения (второй закон Ньютона) может быть записано следующим образом:
|
dV |
|
∂ px |
|
|
∂py |
|
+ ∂ pz |
|
|
ρdxdydz |
= ρdxdydzF + |
∂x |
+ |
∂y |
dxdydz. |
|||||
dt |
||||||||||
|
|
|
|
|
|
∂z |
||||
|
|
|
|
|
|
|
|
|
|
Разделив последнее равенство на dxdydz, получим уравнение движения в напряжениях в векторной форме:
или
dV
dt
dV
dt
+ (V
|
1 |
|
∂px |
|
|
∂py |
|
+ ∂pz |
|
|
= F + |
|
∂x |
+ |
∂y |
|
|||||
|
||||||||||
|
ρ |
|
|
|
|
∂z |
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∂ px |
|
|
∂py |
|
+ ∂ pz |
|
|
)V = F + |
|
∂x |
+ |
∂y |
. |
|||||
|
||||||||||
|
ρ |
|
|
|
|
∂z |
||||
|
|
|
|
|
|
|
|
|
|
|
(5.1)
(5.1,a)
Уравнение движения в напряжениях в проекции на декартовой оси будет иметь следующий вид:
38

dVx
dt dVy dt
dVz dt
+ (V )V |
|
= F + |
1 |
|
∂pxx |
|
+ |
∂p |
|
|
|
+ ∂pzx |
|
|
||||
|
ρ |
|
∂x |
|
yx |
∂y |
, |
|
||||||||||
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|||
+ (V )Vy |
= Fy + |
1 |
|
∂p |
|
|
+ |
∂p |
|
|
+ |
∂p |
|
|
(5.2) |
|||
|
|
|
xy |
∂x |
|
|
yy |
∂y |
|
zy |
, |
|||||||
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
∂z |
|
|||
+ (V )V |
|
= F |
+ |
1 |
|
∂pxz |
|
+ |
∂p |
|
|
|
+ ∂pzz |
|
|
|||
|
ρ |
|
∂x |
|
yz |
∂y |
. |
|
||||||||||
|
z |
z |
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|||
Система (5.2) является незамкнутой даже вместе с уравнением неразрывности, так как число неизвестных (Vx ,Vy ,Vz , pxx , pyy , pzz , pxy , pxz , pzy ) больше числа уравнений.
Для покоящейся жидкости система (5.2) легко замыкается. Вместе с уравнением неразрывности система (5.2) становится полной и в некоторых случаях движения идеальной жидкости и газа. В других случаях требуется привлечь дополнительные связи и гипотезы.
5.2. Дифференциальные уравнения Эйлера для покоящейся жидкости
Рассмотрим жидкость, покоящуюся относительно системы координат, жестко связанной с Землей или движущейся с ускорением относительно нее. Тогда уравнение движения (5.2) примет следующий вид (уравнения Эйлера):
Fx − ρ1 ∂∂px = 0,
|
Fy − |
1 ∂p |
= 0, |
|
|
|
|
|
|
(5.3) |
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
ρ ∂y |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F |
|
− |
1 ∂p |
= 0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
ρ ∂z |
|
|
|
|
|
|
|
|||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
||
или в векторной форме |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F − |
|
|
|
|
grad p = 0. |
|
|
|
|
|
|
(5.4) |
||
|
|
ρ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение (5.4) может быть проинтегрировано, если F является градиентом |
|||||||||||||||
некоторой функции. Пусть |
|
= − ∂Φ ; |
|
|
= − ∂Φ |
|
|
|
= − ∂Φ . |
||||||
→ |
F |
F |
|
; |
F |
|
|||||||||
F = −grad Φ èëè |
y |
z |
|||||||||||||
|
x |
|
|
|
|
|
∂x |
|
|
∂y |
|
|
∂z |
||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
grad Φ + |
|
grad p = 0. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
Для несжимаемой жидкости ( ρ |
= c o n s t ) легко получается общий интеграл |
||||||||||||||
уравнений Эйлера в виде: |
|
|
|
p |
|
|
|
|
|
|
|
|
|
||
|
Φ + |
= const. |
|
|
|
|
|
|
(5.5) |
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
Из (4.3) следует, что поверхности уровня Ф = c o n s t (силовая или потенциальная функция) в покоящейся жидкости совпадают с поверхностями равного давления (изобарическими).
При решении практических задач иногда удобно пользоваться другой формой дифференциального уравнения равновесия жидкостей
39
1 |
dp = Fx dx + Fy dy + Fz dz, |
(5.5) |
|
ρ |
|||
|
|
легко получаемой из системы (5.3).
Задача. Равновесие гибкой нити, нагруженной гидравлическим давлением
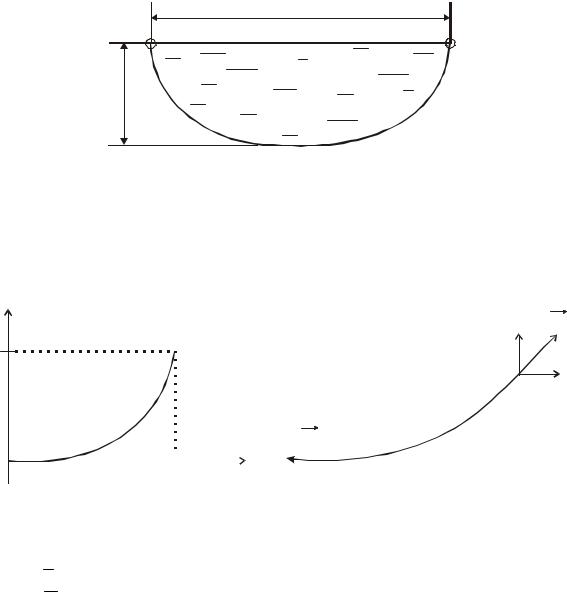
1.1. Постановка задачи. Hайти уравнение линии прогиба невесомой нити под действием давления жидкости. Кроме того, необходимо определить (или вычислить) длину этой линии. Концы нити закреплены на одинаковой высоте, совпадающей с уровнем жидкости. Граничными условиями задачи являются расстояние 2L между концами нити и максимальная величина прогиба у0.
2L
y0
Рис.12. Общий вид линии прогиба
1.2. Вывод уравнения кривой. Введем систему координат с началом в точке максимального прогиба и осью абсцисс параллельной отрезку, соединяющему концы линии. Очевидно, что в данных координатах линия прогиба будет симметричной относительно оси ординат и, следовательно, достаточно рассмотреть участок линии лежащий в первой четверти.
T
Ty
y0
A Tx
0 |
|
H |
|
|
O |
|
L |
|
|
||
|
|
Рис. 13 |
Рассмотрим участок нити ОА от начала координат до какой-либо точки на нити. Сила натяжения приложенная к нити в этой точке противодействует силе
давления P столба жидкости, действующего на выделенный участок, а также силе давления H жидкости, действующей на другую половину нити, находящуюся во
→
второй четверти. Разложим вектор T на составляющие Tx и Ty. Ty противодейству-
→
ет вертикальной составляющей вектора P ! Py. Сила H направлена горизонтально
40
