
Шейпак А.А. Гидравлика и гидропневмопривод (часть 1)
.pdf
в сторону противоположную действию горизонтальной составляющей силы давления. Отсюда видно, что Tx является разницей H − Px . Находим составляющие сил
давления:
Py = ∫x [ y0 |
− y(x)]ρgdx |
0 |
|
y |
|
Px = ∫[ y0 |
− y(x)]ρgdy . |
0 |
|
Отсюда
x
Ty = −Py = −∫[ y0 − y(x)]ρgdx
0
y
Tx = −H + Px = −H + ∫[ y0 − y(x)]ρgdy .
0
→
Далее замечаем , что вектор T в любой точке кривой всегда направлен по каса-
→
тельной к ней, т.е. угол α между T и осью абсцисс является углом наклона касательной. Вследствие того, что tgα равен отношению Ty к Tx имеем:
tgα = |
dy |
= |
Ty |
|
|
||||
dx |
Tx |
||||||||
|
|
|
|
|
|
||||
dy |
|
|
x |
|
|
|
|
|
|
|
|
∫ |
|
|
|||||
|
|
|
|
[ y0 − y(x)]ρgdx |
|||||
|
= |
0 |
|
|
|
|
. |
||
dx |
|
y |
|
||||||
|
H − ∫[ y0 |
− y(x)]ρgdy |
|||||||
|
|
||||||||
|
|
|
|
0 |
|
|
|
|
|
При y0<<L кривизной искомой линии можно пренебречь, т.е. пренебречь Px.
.В этом случае Tx = H, где H − константа.
x
Ty = Py = ∫[ y0 − y(x)]ρgdx
0
Тогда
|
|
|
|
|
x |
|
|
|
|
dy |
|
Ty |
|
∫ |
[ y0 |
− y(x)]ρg |
|
tgα = |
= |
= |
|
|
dx. |
|||
|
|
0 |
|
|
||||
dx |
Tx |
|
|
H |
||||
|
|
|
|
|
|
Вместо константы H подставим h = ρHg :
41
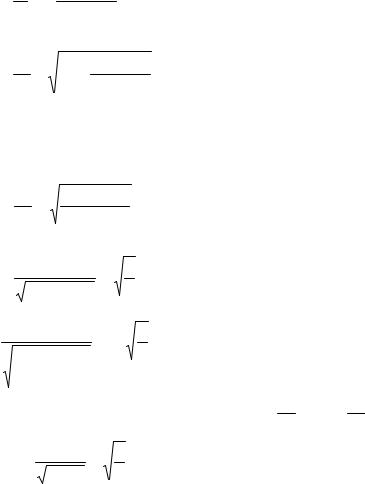
|
|
|
dy |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
∫ |
[ y0 |
|
|
− y(x)] |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
= |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
d 2 y |
= |
|
|
y |
0 |
− y |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
dy |
= t |
|
|
d 2 y |
|
|
= |
|
|
dt |
|
|
|
= |
|
dtdy |
|
= t |
dt |
|
|
|
|||||||||||||||||||
|
dx |
|
|
dx |
2 |
|
|
|
dx |
|
dydx |
dy |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
t |
|
|
dt |
|
|
|
|
|
= |
y0 |
|
− y |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
tdt = |
|
|
|
y0 − y |
dy |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
t |
2 |
|
= − |
[ y |
0 |
− y]2 |
+ C |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2h |
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
dy |
= |
|
|
|
C |
|
|
− |
[ y |
0 |
|
− y]2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
dx |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из условия, что при y=0 → |
dy |
= 0 , находим C |
= |
y0 |
2 |
. |
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
h |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dy |
= |
|
|
|
|
|
y[2y0 |
− y] |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
1 dx |
|
|
|
|
|
||||||||
|
|
|
|
|
y[2y0 |
|
|
− y] |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= y |
0 |
|
1 dx |
|
|
|
|
|
|||||||||
|
|
1−[1− |
|
|
|
y |
|
|
]2 |
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В полученном дифференциальном уравнении заменяем переменные: z=1- y y0
− dz |
= |
1 dx |
1− z 2 |
|
h |
42
;dz = − dy . y0

arcsin z = −x |
1 |
+ C2 |
||
|
|
h |
|
|
1− |
y = sin(C2 |
− x |
1) |
|
|
y0 |
|
|
h |
y = y0 − y0 sin(C2 − x  1h)
1h)
Из условия, что при x=0 y=0, находим C2 = π2
Но с другой стороны, так как при x=L y=y0 получаем y0 = L 1h :
Отсюда можем найти h:
L |
1 |
= |
π |
|
L2 |
= |
π 2 |
h = |
4L2 . |
|
h |
|
2 |
|
h |
|
4 |
|
π 2 |
Подставив h, получим искомое уравнение линии прогиба при y0<<L:
y= y0 − y0 sin((L − x) 2πL ).
Вслучае, когда y0 сопоставимо по величине с L, уже нельзя пренебрегать кривизной линии и, следовательно, нельзя пренебрегать горизонтальной состав-
→
ляющей вектора P - Px. Задача тогда не имеет аналитического решения, но достаточно легко решается численно.
Отметим, что в курсе «Сопротивление материалов» рассматриваются аналогичные задачи о форме равновесия тяжелой нити и о форме нити под действием равномерно распределенной нагрузки.
5.3. Уравнения Навье-Стокса
Предположим, что в пространственном (трехмерном) потоке несжимаемой жидкости имеется следующая зависимость между компонентами тензора напряжений и тензора скоростей деформаций:
|
|
∂Vx |
|
|
|
|
|
|
∂Vx |
|
|
∂V |
y |
|
|
||||
pxx = −p + 2µ |
, |
|
|
|
|
+ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
∂x |
|
pxy = pxy = µ |
|
∂y |
∂x |
, |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
∂Vy |
|
|
|
|
|
|
∂V |
x |
|
|
∂V |
z |
|
|
|
||
pyy = −p + 2µ |
|
|
|
, |
|
pxz = pzx = µ |
|
|
|
+ |
|
, |
(5.7) |
||||||
∂y |
|
|
∂z |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
|
||||||||
|
|
∂Vz |
|
|
|
|
|
|
∂V |
y |
|
|
∂Vz |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
pzz = −p + 2µ |
|
, |
|
|
|
|
+ |
|
|
||||||||||
∂z |
|
pyz = pzy = µ |
|
∂z |
|
∂y |
, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где p – термодинамическое давление. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из первых трех уравнений следует, что |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
p = − |
pxx + pyy + pzz |
. |
|
|
|
|
|
|
|
|
|
|
(5.8) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Система зависимостей (5.7) является обобщением закона жидкостного трения Ньютона. Она непосредственно не проверяется экспериментально, однако, все следствия из этой гипотезы на основе точных решений дифференциальных уравнений движения жидкости не противоречат опытным данным.
43

Существует более строгое обоснование гипотезы для обобщенного закона трения Ньютона, но оно требует хорошего знания тензорного исчисления, которое не входит в программу высшей математики для большинства машиностроительных специальностей.
Подставляя зависимости (5.7) в уравнение движения в напряжениях (5.2), можно получить дифференциальные уравнения движения для несжимаемой вязкой жидкости (уравнение Навье-Стокса).
|
∂V |
|
|
|
|
|
|
|
|
|
1 ∂p |
|
|
|
|
|
|
|
|
||||||||
|
x |
|
+ (V )Vx |
= Fx − |
|
|
|
|
|
|
|
+ν 2Vx , |
|
||||||||||||||
|
∂t |
|
|
ρ ∂x |
|
||||||||||||||||||||||
|
∂Vy |
+ (V )Vy |
= Fy − |
|
|
1 ∂p |
+ν 2Vy , |
(5.9) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
ρ ∂y |
||||||||||||||||||||||
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
∂V |
|
|
|
|
|
|
|
|
1 ∂p |
|
|
|
|
|
|
|
|
|||||||||
|
z |
+ (V )Vz |
= Fz − |
|
|
|
|
|
|
+ν 2Vz , |
|
||||||||||||||||
|
∂t |
|
|
ρ ∂z |
|
||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
∂2Vx |
|
|
∂2Vx |
|
|
|
|
∂2Vx |
|
|
|
||||||||||||||
|
Vx = ∆Vx = |
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
, |
|
||||||||||
|
|
|
∂x2 |
|
|
∂y2 |
|
|
∂z2 |
|
|||||||||||||||||
2 |
|
|
∂2Vy |
|
|
|
∂2Vy |
|
|
|
|
|
∂2Vy |
|
|
(5.10) |
|||||||||||
|
Vy = ∆Vy = |
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
, |
|||||||
|
|
|
∂x2 |
|
|
|
|
∂y2 |
|
|
|
∂z2 |
|
||||||||||||||
2 |
|
∂2Vz |
|
|
∂2Vz |
|
|
|
∂2Vz |
|
|
|
|||||||||||||||
|
Vz = ∆Vz = |
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|||||||||||
|
|
|
∂x2 |
|
|
∂y2 |
|
|
|
∂z2 |
|
|
|
|
|||||||||||||
– лапласианы соответствующих компонентов скоростей.
Ниже представлены выкладки получения одного уравнения из системы (5.9) для оси X
∂p |
xx + |
∂pyx |
|
+ |
∂p |
zx |
= − |
∂p |
+ 2µ |
∂ |
2V |
x |
+ µ |
∂2V |
x |
|||||
|
∂y |
|
|
∂x |
|
|
|
|
||||||||||||
∂x |
|
∂z |
|
|
|
∂x2 |
|
|
|
|
∂y2 |
|||||||||
|
|
|
∂ |
2 |
|
|
2 |
|
2 |
|
|
|
|
|
∂ |
|
|
|
||
= − ∂p |
+ µ |
Vx |
+ |
∂ Vx + |
∂ Vx |
+ µ |
|
|
∂Vx |
|||||||||||
|
|
|
|
|||||||||||||||||
|
∂x |
|
∂x |
2 |
|
∂y |
2 |
∂z |
2 |
|
|
|
|
∂x |
|
∂x |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
+ µ |
∂2Vy |
+ |
µ |
∂2V |
x + µ |
∂2V |
z |
= |
|||||
∂x∂y |
|
|
|
||||||||||
|
|
|
|
|
∂z2 |
∂x∂z |
|
||||||
|
∂V |
y |
|
|
|
|
|
|
|
|
|
||
+ |
|
|
+ |
∂Vz |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
∂y |
|
∂z |
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
Последнее слагаемое для несжимаемой жидкости равно нулю.
В векторной форме уравнение Навье-Стокса записывается следующим обра-
зом:
∂V |
+ (V )V = F − |
1 |
grad p +ν 2V. |
(5.10) |
|
∂t |
ρ |
||||
|
|
|
Уравнение Навье-Стокса вместе с уравнением неразрывности div V = ∂∂Vxx + ∂∂Vyy + ∂∂Vzz = 0
образуют для несжимаемой жидкости замкнутую систему и вместе с граничными и начальными условиями принципиально позволяют получить решение всех задач механики жидкости для ламинарного режима течения. Граничные условия для вязкой жидкости сводятся к “прилипанию“ частиц жидкости к стенке. Опыт показывает, что частицы жидкости и газа не проскальзывают по стенке, приобретая значение ее скорости. Это условие не зависит от смачиваемости или несмачиваемости стенки жидкостью. Однако при течении разреженных газов граничные условия изменяются. О.А.Ладыженская и ряд других исследователей показали, что система уравнений
44
Навье-Стокса имеет единственное решение для плоского потока. Для трехмерного случая теорема существования и единственности имеет ряд ограничений.
Следует отметить, что существует небольшое число точных (аналитических) решений уравнений Навье-Стокса. Большинство из них относится к достаточно простым каналам, когда существенно не проявляется нелинейность этой системы.
В последнее время много задач было решено с помощью ЭВМ различными численными методами.
5.4.Некоторые точные решения уравнения Навье-Стокса
Внастоящем учебном пособии приведены некоторые решения, имеющие практическое значение. Более подробные сведения приведены в ряде работ [5, 11, 12, 17, 18 ].
5.4.1.Установившееся движение жидкости в прямой трубе
эллиптического сечения
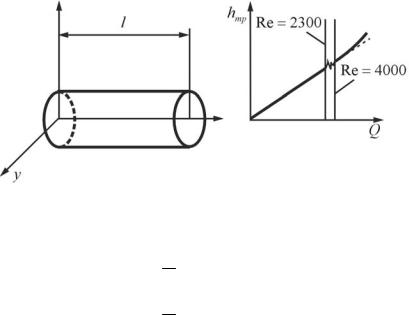
Будем рассматривать так называемое стабилизированное течение, когда профили скоростей в каждом сечении трубы идентичны. Такой случай, строго говоря, соответствует трубе бесконечной длины. Линии тока будем полагать прямыми линиями, параллельными оси трубы, которую совместим с осью Z (рис. 14).
x
z
Рис. 14. Установившееся движение в прямой трубе эллиптического сечения
Система (5.9) для нашего случая сведется к следующей:
O = − ρ1 ∂∂px ,
O = − ρ1 ∂∂py ,
|
1 |
∂p |
|
2 |
|
|
2 |
|
|
|
O = − |
|
∂ Vz |
+ |
∂ Vz |
||||||
|
|
|||||||||
ρ |
∂z |
+ν |
∂x |
2 |
∂y |
2 |
. |
|||
|
|
|
|
|
|
|||||
Очевидно, в рассматриваемой задаче давление может быть функцией только переменной z, а компонента скорости Vz – функцией переменных x и y.
Математическая модель рассматриваемой гидромеханической задачи сведется к следующему уравнению:
|
2 |
|
|
2 |
|
|
|
dp |
|
∆p |
|
|
|
∂ Vz |
+ |
∂ Vz |
= |
= − |
|
|
|||||
µ |
|
|
|
|
|
|
|
, |
(5.11) |
|||
∂x |
2 |
∂y |
2 |
dz |
l |
|||||||
|
|
|
|
|
|
|
|
|
||||
где ∆p = p1 − p2 .
45

Так как левая часть уравнения является функцией x и y, а правая – z, то они равны некоторой постоянной.
Будем искать решение в виде:
Vz = A 1− x2 a2 − y2 b2 ,
удовлетворяющее граничным условиям на границе эллипса с уравнением x2 a2 + y2 b2 = 1. Подставляя Vz в (5.11), найдем постоянную A
A = |
∆p |
|
a2b2 |
=V |
z max |
. |
|
2µl |
a2 +b2 |
||||||
|
|
|
|
Вычислим расход, проходящий через произвольное поперечное сечение
|
Q = |
∫∫ |
V |
dxdy =V |
|
|
∫∫ |
|
− x |
2 |
|
|
− y |
2 |
|
|
|
|
|
|
||||||
|
|
|
1 |
|
a2 |
|
b2 |
dxdy. |
|
|
||||||||||||||||
|
|
|
z |
|
|
|
|
|
z max |
|
|
|
|
|
|
|
|
|
|
|||||||
Пусть |
′ |
′ |
|
′ |
= |
|
x |
′2 |
|
+ y |
′2 |
|
′ |
|
′ |
= |
|
|
′ |
′ |
|
|
|
|
|
|
x = ax , y = ay , r |
|
|
|
|
|
, dx dy |
|
2πr dr . |
|
|
|
|
||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
π |
|
Q =Vz maxab∫∫(1− x |
′2 |
− y |
′2 |
|
′ |
′ |
=Vz maxab∫(1−r |
′2 |
|
′ |
′ |
= |
Vz maxab. |
|||||||||||||
|
|
)dx dy |
|
)2πr dr |
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Средняя скорость по сечению будет
V |
z ср |
= |
|
Q |
= |
Vz max |
. |
πab |
|
||||||
|
|
2 |
|
||||
Если a = b = r = d/2, то для трубы круглого сечения получим
Q = |
πd 4∆p |
= |
πd 2 |
|
dd ∆p |
. |
|
|
|
||||||
128µl |
4 |
32 |
ρlν |
|
|
|
|||||||||
Откуда |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆p = λ |
l |
ρ |
V 2 |
|
èëè h |
òð |
= λ |
l |
|
V |
2 |
, |
|||
d |
2 |
|
d |
|
|
2g |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
(5.12)
(5.13)
где
λ = |
64 |
и Re = |
Vd |
. |
(5.14) |
Re |
|
||||
|
|
ν |
|
||
Зависимость (5.12) носит название формулы Пуазейля. Число Рейнольдса Re является безразмерным комплексом. Формула (5.12) хорошо подтверждается экспериментом, пока число Рейнольдса Re ≤ 2300 (см. рис. 14 справа). До этого значения течение жидкости в трубе носит ламинарный характер, при числе Re > 4000 течение в трубе, как правило, становится турбулентным. При этом зависимость потерь на трение (или давление трения) от расхода (средней скорости) становится существенно нелинейной, близкой к квадратичной. Подробнее этот вопрос целесообразно изучать при выполнении лабораторной работы по экспериментальному определению коэффициента гидравлического трения.
46
5.4.2. Установившееся движение между двумя параллельными пластинами
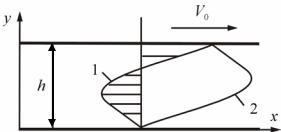
Рассмотрим течение в канале, ограниченном двумя параллельными пластинами бесконечной протяженности (рис. 15).
Рис. 15. Течение жидкости в зазоре между параллельными пластинами
Система уравнений (5.9) для этого случая принимает следующий вид:
dp |
= µ |
d 2Vx |
. |
(5.15) |
dx |
2 |
|||
|
dy |
|
||
Будем полагать, что нижняя пластина покоится, а верхняя движется с постоянной скоростью V0 . Такое течение в общем случае с наличием градиента давления
называется течением Куэтта. Пусть расстояние между пластинами будет h. Граничные условия примут следующий вид:
|
y = 0, |
|
V = 0; |
|
|
|
|
||||||
Решение уравнения будет |
y = h, |
|
V =V0. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V =V0 |
y |
− |
h2 |
|
y |
− |
y |
|
∆p |
|
(5.16) |
||
|
|
|
|
1 |
|
|
|
|
. |
||||
h |
|
|
h |
l |
|||||||||
|
|
2µ h |
|
|
|
|
|||||||
Распределение скоростей в соответствии с этим решением приведено на рис.15: кривая 1 соответствует большому положительному градиенту давления, кривая 2 – отрицательному.
При безградиентном течении (течение чистого сдвига) получается линейное
распределение скоростей: |
y |
|
|
|
V =V0 |
. |
(5.17) |
||
|
||||
|
h |
|
||
Если обе пластины неподвижны и рассматривается участок канала длиною l в направлении оси x, распределение скоростей будет
V |
|
= |
h2 |
∆p y |
1− |
y |
(5.18) |
|||
x |
|
|
|
|
|
. |
||||
|
|
|
|
|||||||
|
|
|
2µ |
l h |
|
h |
|
|||
Подсчитаем величину расхода через канал, имеющий толщину h и ширину вдоль оси z b, предполагая закон распределения скоростей (5.18).
h |
h |
∆ph |
|
y |
∆ph3b |
|
|
|
Q = b∫Vxdy = b∫ |
1 |
− |
|
ydy = |
12µl |
. |
(5.19) |
|
|
||||||||
0 |
0 |
2µl |
|
h |
|
|
||
Уравнение (5.19) хорошо подтверждается экспериментами при условии ламинарного режима течения и b>>h, l>>h, что выполняется при течении в зазорах.
Отметим, как и в предыдущей задаче, линейную зависимость расхода от перепада давления. Это – общая закономерность ламинарного движения жидкости.
47
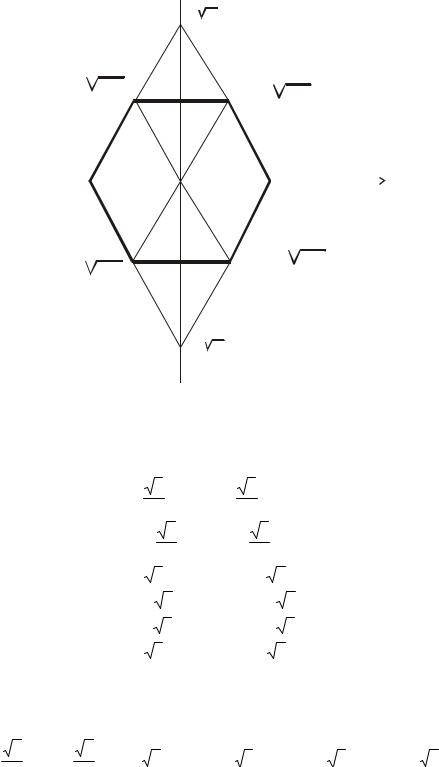
5.4.3. Установившееся течение в трубе с сечением в виде правильного шестиугольника
Трубы такой формы часто используются для различных теплообменных устройств. Решение получено методом, подобному тому, с помощью которого обычно получают расчетную формулу для трубы с сечением в виде правильного треугольника.
y 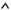 a 3
a 3
-a/2,a |
3/2 |
|
a/2,a 3/2 |
|
|
|
|
||
|
a |
|
a |
|
|
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|
-a,0 |
|
0 |
a,0 |
x |
a |
|
|||
|
|
a |
|
|
-a/2,-a |
3/2 |
|
a/2,-a |
3/2 |
|
|
|
||
-a 3
Рис. 16. Расчетная схема поперечного сечения трубы
Составим уравнения прямых, образующих стороны правильного шестиугольника со стороной a :
1. |
y = |
|
3 a èëè y − |
|
3 a = 0 |
|
|
2 |
2 |
||
2. |
y = − |
3 a èëè y + |
3 a = 0 |
||
|
|
|
2 |
|
2 |
3. |
y = |
|
3(a − x) èëè |
y − 3(a − x)= 0 |
|
4. |
y = − |
3(a − x) èëè |
y + 3(a − x)= 0 |
||
5. |
y = − |
3(a + x) èëè |
|
y + 3(a + x)= 0 |
|
6. |
y = |
|
3(a + x) èëè |
y − 3(a + x)= 0 |
|
Решение, удовлетворяющее граничному условию обращения в нуль на контуре сечения скорости, будет
|
|
|
|
|
(a − x))(y + 3(a + x))(y − 3(a + x)). |
V (x, y)= A y − |
3 a y + |
3 a (y − 3(a − x))(y + 3 |
|||
|
2 |
|
2 |
|
|
|
|
|
|
||
48

Постоянную А определим из условия равенства лапласиана V (x, y) величине - ∆p /(µl). A = −∆p /(54µla4 ). Объемный расход определяем как
Q = ∫∫V (x, y)dxdy . |
(5.20) |
A |
|
После простых, но длительных выкладок получаем следующую расчетную формулу для объемного расхода:
Q = |
0,316a4 ∆p |
. |
(5.21) |
|
|||
|
µl |
|
|
Для трубы с радиусом, описанным вокруг шестиугольника (r=a) формула для расхода будет
Q = |
0,393a4 ∆p |
. |
(5.22) |
|
|||
|
µl |
|
|
Для трубы с радиусом, вписанным в шестиугольник (r=a  3 /2), формула для расхода будет
3 /2), формула для расхода будет
Q = |
0,221a4 ∆p |
. |
(5.23) |
|
|||
|
µl |
|
|
5.4.4.Первая задача Стокса
Вкачестве примера использования уравнений Навье-Стокса для нестационарного движения рассмотрим течение жидкости, которое возникает при внезапном движении ранее покоившейся плоской стенки в своей плоскости с постоянной скоростью V0 . Пусть стенка совпадает с плоскостью XZ (см. рис. 15). Подобная за-
дача является модельной для расчета разгона различных устройств гидроавтоматики, например, плоских затворов.
Для плоской задачи из уравнения Навье-Стокса остается уравнение типа уравнения теплопроводности:
∂V |
=ν |
∂2V . |
(5.24) |
∂t |
|
∂y2 |
|
Давление во всем пространстве постоянное. Начальные и граничные условия можно сформулировать следующим образом:
при t ≤ 0, V = 0 для всех y;
при t > 0, V = V0 для y = 0; V = 0 для y = ∞.
Решение уравнения (5.24) подробно рассматривается в курсе высшей математики.
Если ввести безразмерную переменную |
|
|
η = |
y |
(5.25) |
2 |
νt |
|
и положить |
|
|
V =V0 f (η), |
(5.26) |
|
|
|
49 |
уравнение в частных производных (5.24) можно свести к обыкновенному дифференциальному уравнению:
f ′′+ 2ηf ′ = 0
со следующими граничными условиями:
|
f =1приη = 0 и f = 0 приη |
Решением этого уравнения будет |
|
|
V =V0erfcη , |
где |
|
erfcη = |
2 ∞∫exp(−η2 )dη =1− erf η =1− |
|
π η |
(5.27)
= ∞.
(5.28)
2 |
η |
∫exp(−η2 )dη |
|
π |
0 |
является дополнительным интегралом вероятности. Для функций erf и erfc имеются подробные таблицы. Значение erfc при η = 2 равно примерно 0.01. Поэтому толщи-
на слоя жидкости, увлекаемая пластиной, может быть оценена как:
δ = 2η νt ≈ 4 νt. |
(5.29) |
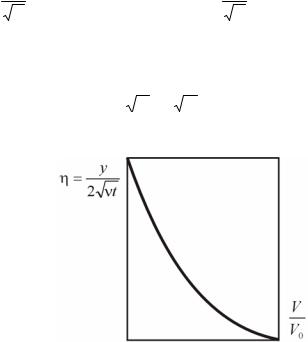
Графическая зависимость распределения скоростей приведена на рис. 17.
Рис. 17. Распределение скоростей вблизи стенки
5.5. Уравнение движения Рейнольдса для турбулентного режима течения вязкой жидкости
Уравнения движения Навье-Стокса справедливы лишь для ламинарного режима течения. При турбулентном режиме течения локальную скорость можно представить в виде суммы осредненной во времени скорости и пульсации скорости:
|
|
~ |
|
|
′ |
(5.30) |
|
|
|
|
|||
~ |
V =V |
+V , |
||||
– мгновенное значение скорости; |
|
|
||||
где V |
|
|
||||
|
|
– осредненное значение скорости; |
|
|||
V |
|
|||||
V ′ |
– пульсация скорости. |
|
|
|||
Покажем, что наличие пульсаций скорости приводит к появлению дополнительных поверхностных напряжений. Пусть жидкость движется в основном вдоль оси Х, но пульсации скорости имеют пространственный характер. В направлении оси У за время δ t переносится масса жидкости ρVy′δA δt с импульсом ρVy′Vx′δA δt .
Приравнивая его импульсу сил – τ′xyδA δt , получим мгновенное значение касательного напряжения
′ |
′ ′ |
(5.31) |
τxy = −ρVyVx . |
||
50
