Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Гидравлика и гидропривод

Файл:

Шейпак А.А. Гидравлика и гидропневмопривод (часть 1)

.pdf

Скачиваний:

1018

Добавлен:

02.05.2014

Размер:

4.79 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2016 17 18 19 20 > Следующая >>>

15.3.11.

Определить с точностью до ε=0,1мм диаметр сопла для подачи смазочноохлaждающей жидкости в зону резания с постоянным напором, если избыточное давление Р=0,01 МПа. Вязкость жидкости υ=1,3 сСт. Коэффициент расхода сопла

описывается эмпирической формулой: µ =1− 50Re,5 .

15.3.12.

Определить диаметр d трубопровода длиной l=9 м, соединен- ного последовательно с трубопроводом диаметром D=60 мм, длина которого L=2 м. Эквивалентная шероховатость обоих тру- бопроводов ∆=0,005 мм; расход жидкости Q=300 л/мин, разность

давлений в начальном и конечном сечениях ∆р=105 Н/м2; вязкость υ=1,9 10−6 м2/с; плотность ρ=1000 кг/м3.

15.3.13.

Определить расход керосина в гладкой горизонтальной трубе длиной l=40 м; диаметром d=40 мм, если разность давлений в начальном и конечном сечениях трубы ∆р=160 кПа. Вязкость керосина υ=0,02 Ст; плотность ρ=800 кг/м3.

15.3.14.

Определить расход жидкости в трубопроводе постоянного сечения через 0,1 секунды после начала течения, если сум- 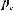марный коэффициент местных потерь ζ=2, плотность жидкости ρ=1000 кг/м3, кинематический коэффициент вязкости

υ=0,02 ст, длина трубопровода L=4 м, его диаметр d=0,04 м. Истечение происходит в атмосферу. Избыточное давление на входе изменяется по формуле Рвх=10000t Па, где t – время. Движение считать неустановившимся, жидкость – несжимаемой.

15.3.15.

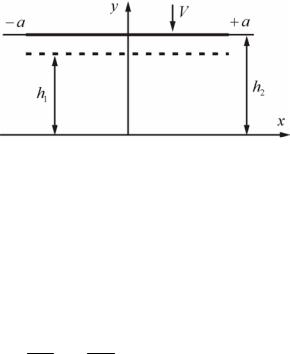
Определить время опорожнения бака через шланг постоянного диаметра d=20 мм, длиной l=20 мм, с учетом инерционного напора жидкости. Сравнить полученную зависимость скорости от времени с зависимостью, полученную без учета инерционного напора. Начальный уровень жидкости Н0=1 м; коэффициент гидравлических потерь ζ=1; площадь поперечного сечения бака S=0,0314 м2. Начальные условия записать при мгновенном открытии затвора. Ответ дать в секундах.

151

16.ТЕЧЕНИЕ ЖИДКОСТИ В ЗАЗОРАХ МАШИН И АППАРАТОВ

16.1.Гидромеханическая модель опорного подшипника

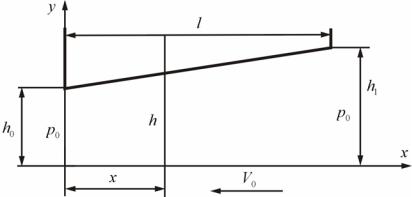
Рассмотрим сдавливание слоя параллельными плоскостями. Пусть элемент верхней плоскости с координатами ± a , параллельный оси X, перемещается вертикально вниз со скоростью V (рис. 57). Граничные условия системы уравнений смазочного слоя для рассматриваемой задачи примут следующий вид:

y = 0,	Vx = 0, Vy = 0;
y = h,	Vx = 0, Vy = -V;		(16.1)
x = ± a , p = p0 , x = 0,		∂p	= 0.
		∂x

Рис. 57. Сдавливание слоя жидкости параллельными плоскостями

Решение для компоненты скорости Vx ищем в следующем виде:

Vx =	1	∂p y2	+ C1 y + C2 .	(16.2)

	2µ ∂x

Принимая во внимание граничные условия, получим:

Vx =	1	∂p y(y −h).	(16.3)

	2µ ∂x

Из уравнения неразрывности имеем:

∂∂Vxx dy + ∂∂Vyy dy = 0,

h ∂V				h	∂Vy
∫			x dy + ∫				dy	= 0,
∫			x dy + ∫				dy	= 0,
0	∂x			0	∂y
∂		h				0h = 0,
∂		∫0 Vx dy +Vy
∂x
∂x
∂		h
		Vx dy −V = 0.
		Vx dy −V = 0.
∂x ∫0

Произведя интегрирование, получим:

∂	1 ∂p h	3	=V.


	2µ ∂x 6
∂x

Если µ = c o n s t a n t , то

152

∂2 p	= −	12Vµ
∂x2	= −	h3
∂x2		h3
è		(16.4)

p = − 6hV3µ x2 + C1 x + C2 x.

Учитывая граничные условия для давления, получим:

p = p0	+	6Vµ	(a2	− x2 ).	(16.5)

		h3

Определим теперь силу, действующую на пластину шириною b в направлении оси Z.

+a 6Vµb			(a	2		2	)dx =	8Va3bµ
P = ∫					− x					.	(16.6)
P = ∫	h	3			− x			h	3	.	(16.6)
−a	h							h

Среднее давление будет

pср

4Va2

2ab

Максимальное давление

pmax =

6Va2µ

Так как ∂p

= −12Vµx

3 , то

∂x

= −

xy( y −h).

Используя уравнение неразрывности, получим:

	6V		y	3		y	2	h
Vy =					−				+ C.
	h	3	3			2

(16.7)

(16.8)

(16.9,а)

Учитывая граничное условие Vy = 0 при у = 0, окончательно имеем:

	6V		y	3		y	2	h
Vy =					−
									.	(16.9,б)
	h	3	3			2

Если у = h, то Vy = -V.

Если рассматривается круглая пластина радиусом a, то решение будет сле-

дующим:

3Vµ

(a2

− r 2 ),

p = p0 +

(16.10)

Va4

P =

πµ

(16.11)

pср =

3Va2 µ

(16.12)

2h3

pmax

3Va2 µ

16.2. Плоский клиновидный слой смазки

Это – движение жидкости между двумя непараллельными плоскостями, одна из которых перемещается с постоянной скоростью V0 в направлении отрицательной

153

оси X. Рассматриваемая задача является простейшей гидромеханической моделью подшипника скольжения. Граничные условия для системы (9.5) будут следующими

(рис. 58):

при y = 0, Vx = -V0 , Vy = 0;

при y = h, Vx = 0, Vy = 0;	(16.13)
при x = 0, x = l, (h= h0 и h1 , соответственно) p= p0 .

Рис. 58. Плоский клиновидный слой смазки

Решение для компоненты скорости Vx

ищем в следующем виде:

Vx =

∂p y2 + C1 y + C2 .

(16.14)

2µ ∂x

Учитывая граничные условия и связь между геометрией канала

h −h

h = h +

x = h

+ k

, где k =

1 0

получим:

∂p

y( y

− h)

−V0 1

−

(16.15)

2µ ∂x

Для нахождения давления используем, как в предыдущей задаче, уравнение неразрывности.

h	∂V	x	h	∂Vy
∫			dy + ∫		dy = 0 .
	∂x			∂y
0			0

После несложных преобразований приходим к следующему равенству:

∂	h3 ∂p		V		h
		+		0		= 0.	(16.16)

	12µ ∂x		2
∂x

Так как выражение в скобках не зависит от х и у, его можно приравнять произвольной постоянной, которую целесообразно выбрать следующим образом:

h3 ∂p	+	V		h	=	V h			(16.17)
			0				0	.
12µ ∂x		2				2

Очевидно, что при h = h давление достигает экстремума, являющегося мак-

симумом.

Уравнение (16.17) можно переписать следующим образом:

∂p	= −6V	µ	h −h	.	(16.18)
∂x
	0		h3

154

Учитывая, что ∂p

∂x

= ∂p

∂h

∂x

, вместо (16.18) получим

∂h

∂p

= −

6V µl 1

−

∂h

Интегрируя с учетом граничных условий, получим

p = p

6V0 µl

−

1+ k

l 2

kh2

l + kx

2 + k

+ k

(l + kx)2

(16.19)

(16.20)

Вычислим силу давления, принимая размер в направлении оси Z, равным b.

P = ∫l (p − p0 )bdx.

После вычисления интеграла получим

P =	6V µl2b			+ k) −	2k
	0		ln(1			.	(16.21)
	2	2
	k	h0			2 + k

Исследуя зависимость силы давления от параметра клиновидного слоя k, можно получить, что значение максимума силы соответствует k = 1.2 и

Pmax = 0.16µV0	l 2b
			.	(16.22)
	h	2
	0

Для отыскания координаты приложения силы P xL составим уравнение момен-

тов:

P xL = ∫l (p − p0 ) xdx.	(16.23)
0

Из уравнения (16.23) получим

xL =	6k + k 2	− 2(3 + 2k ) ln(1+ k )	. l	(16.24)
	2k[(2	+ k ) ln(1+ k )− 2k]

Когда P = Pmax , x = 0.43l.

Используя закон распределения скорости (16.15), получим

Исключая h и ∂∂px

	∂V				V		0		h ∂p
τ = µ		x		= µ			0	−		.
τ = µ		x		= µ				−		.
	∂y					h 2 ∂x
	∂y		y=0			h 2 ∂x

, после упрощений найдем, что

τ = µ	V0		4l	−	6(1+ k )	l2	.
						2
	h				2 + k
		l + kx				(l + kx)

(16.25)

(16.26)

Сила трения будет

l	V	µlb		4	ln(1	+ k )−	6
T = ∫τbdx =
	0							.	(16.27)
	h0
0			k				2 + k

При k = 1.2 , T ≈ 0.75V0 µlb . h0

Отметим, что в клиновидном смазочном слое возможно образование возвратного течения (отрыва потока). Координата точки отрыва определяется из условия

	∂Vx	=0
	∂y
		y=h

и равна

155

2k +1
xотр = k(k + 2)l.	(16.28)

Очевидно, что при k ≤1 xотр ≥ l , т.е. течение по всей длине пластины будет безотрывным. При k = 1.2 отрыв происходит в точке xотр = 0,89. Если k = 1, то зна-

чения сил давления и трения мало отличаются от их значений при k = 1,2. Отметим, что сила давления обратно пропорциональна квадрату малой вели-

чины h0 , а сила трения обратно пропорциональна этой же величине в первой степе-

ни.

16.3. Основные сведения по работе цилиндрического подшипника скольжения

При установившемся движении шипа в подшипнике линия наименьшего зазора между ними смещается в сторону вращения шипа и расположена приближенно перпендикулярно к направлению внешней нагрузки на шип.

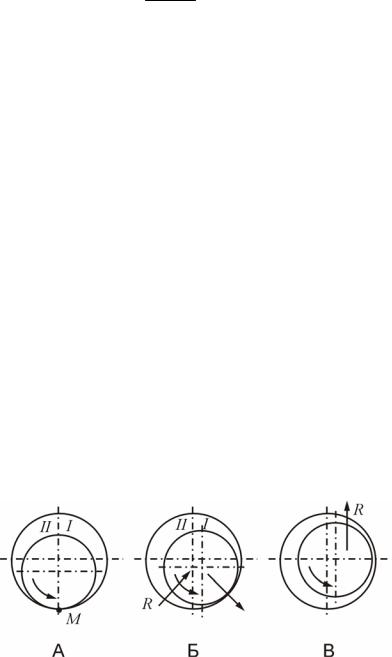
Пусть нагрузка на горизонтальный вал, вращающийся в подшипнике, направлена по вертикали. До вращения вала его шип будет касаться поверхности вкладыша подшипника в некоторой точке M (рис. 59, А). Область между поверхностями шипа и подшипника разделена на две равные части I и II. В первой части движение поверхности шипа будет происходить в сторону широкой части слоя, поэтому результирующая сила давления будет направлена от шипа к вкладышу (рис. 59, Б). Во второй части, наоборот, результирующая сила давления будет направлена от вкладыша к шипу (рис. 59, В). Так как эти силы не уравновешиваются внешней нагрузкой, то шип будет смещаться вправо, пока направление равнодействующей силы давления не будет противоположным внешней нагрузке.

Рис. 59. Цилиндрический подшипник скольжения

16.4. Поток утечек через неподвижное уплотнение

Рассмотрим в приближении Рейнольдса поток утечек через неподвижное уплотнение в рамках плоской модели канала с одной гладкой и одной произвольной шероховатой поверхностью.

Система уравнений и граничные условия представлены ниже.

∂p	= µ	∂2Vx	,	∂p	= 0,	∂Vx	+	∂Vy	= 0
∂x				∂y				∂y
		∂y2				∂x

x = 0, y = h1	, p = p1	;	(16.29)
x =1, y = h2 , p = p2 ;			(16.29)
x =1, y = h2 , p = p2 ;

156

h(x) << x1 − x2 =1.

Ищем решение в виде:

= (1/ 2µ)(∂p / ∂x) y( y − h) .

Из уравнения неразрывности

∂V

∂Vy

∂ h

= 0 .

∫

dy +∫

dy =

или

Vx dy

∂x

∂y

∂x ∫0

После интегрирования получим

∂

1 h

(x) ∂p

= 0 .

∂x

2µ

∂x

Если µ = const , то

1 h3 (x) ∂

2 p

1 3h2 (x) dh ∂p

= 0

;

2µ 6 ∂x2

2µ

6 dx ∂x

(16.30)

d 2 p

dh dp

h(x)

= 0.

dx2

dx dx

При произвольной функции h(x) (16.30) лучше всего решать методом прогон-

ки. Обозначив

= z,

d 2 p

∂z

, получим

∂x

dx2

h(x)

+ 3z

= 0,

h(x)

ln z + ln[h(x)]				= ln C z1/ 3h(x) = C z h3 (x) = C ,
									1
3	(x)	dp	= C1 ,	dp =	C1dx	, dp =	C1dx	, p	= C1 ∫	dx	+ C2 .
		dx			h3 (x)		h3 (x)			h3 (x)

В общем случае

x dξ

p(x) = C1 ∫0 h3 (ξ) + C2 .

При x = 0 выполняется граничное условие p = p1 C2 = p1 .

При x =1 выполняется граничное условие p = p2 .

		l	dξ
p2 = C1 ∫0				+ p1	,
p2 = C1 ∫0			h3 (ξ)	+ p1	,
C1 =		p2 − p1
C1 =	∫l	dξ / h3 (ξ)
	∫l	dξ / h3 (ξ)
0

157

Продифференцируем общую формулу ∂p

и подставим коэффици-

h3 (x)

∂x

енты:

p2 − p1

;

h3 ∫l

dξ / h3 (ξ)

∂p

1 ∂p

∂p

Q = ∫Vx dy = ∫

y( y

− h) dy =

∫y( y − h) dy =

−

;

2µ

∂x

2µ ∂x

Q = −

или, подставляя первую производную давления:

12µ dx

− p

Q = −12µ

h3 ∫dξ / h3 (ξ)

12µ∫dξ / h3 (ξ)

Рассмотрим течение через клиновидный зазор (линейная функция h(x)). Под-

ставим в уравнение для утечек h(x) = h1 + kx,

где k = (h2 − h1 ) / l . В таком случае

= −

1 1

+ C2 ,

∫h3 (x)

∫(h

+ k x)3

k 2 (h + kx)2

p = −C

+ C

+ kx)2

1 2k (h

C = −

2k( p

− p

2 h2

= p −

( p

− p

)h2

1 2

2 − h

− h2

p = p

2 h2

( p

− p

)

−

( p

− p

)h2

1 2

(h22 − h12 )(h1 + k x)2

h22 − h12

( p

− p )

h2 h

p = p1

1 2

− h22 ,

(h22 − h12 )

(h1 + k x)2

2k( p

− p )h

2 h2

k =

− h )

= −

(h22 − h12 )(h1 + k x)3

Удельные утечки на единицу ширины (м2/с) составят

Q =

( p

− p )h2 h

(м2 /c)

(16.31)

(h2

+ h1 )µ

Из рассмотренного решения ясно, что в модели Рейнольдса с неподвижными поверхностями невозможен отрыв потока: конфузорные и диффузорные каналы имеют при всех прочих равных условиях одинаковое значение коэффициентов потерь, что при достаточно больших числах Рейнольдса может привести к значительному завышению величины расхода.

Рассмотрим теперь			течение			в	щели со			средним значением зазора
h1 + h2 = 2		= const . Тогда h1	=		+ hT (x),	h2	=		− hT (x),	где hT (x) - шероховатость.
	h			h				h

158

(

+ hT (x))2 (

− hT (x))2 = [(

+ hT (x))(

− hT (x))]2

= (

2 − h (x)2 )2

4 − 2

2 h (x)2 + h (x)4

Тогда:

(p1 − p2 )(

2 − hT (x)2 )2

(16.32)

Q = −

(м

/с) .

12lµ h

При отсутствии шероховатости получим каноническую формулу:

	(p	− p		)		3
			2		h
Q = −	1						(м2 /с) .	(16.33)
		12lµ

Таким образом, следует вывод, что при увеличении шероховатости утечки при прочих равных условиях должны уменьшаться.

16.5. Течение жидкости с вязкостью, зависящей от давления

Рассмотрим сдавливание слоя жидкости параллельными плоскостями. Пусть элемент верхней плоскости с координатами ± а, параллельный оси х, перемещается вертикально вниз со скоростью V. Граничные условия для рассматриваемой задачи известны (16.1). Из уравнения неразрывности имеем решение для

µ = µ 0 =const.

		0		h 3 (	)
p =	p		+	6Vµ	a 2 − x 2 .	(16.34)

Если µ = µeα(p− p0 ) ,				∂p
то			1		= −
			2µ0eα( p− p0 ) ∂x

		e −α (p − p 0 )dp = −
−	1	e −α (p − p 0 )d[− α(p −

	α

(16.35)

6Vx
	h3
12 V µ 0 x			dx
	h 3		dx
	h 3
	p 0 )]=	12Vµ			0	x	dx
					0
			h	3
			h

e −α (p − p 0 )+ c =

6 V µ 0 x 2

x = ±a,

p = p

h 3

+ c =

6 V µ 0 a 2

h 3

c =

6 V µ 0

a 2 −

h 3

−

6Vµ

0 a

−α (p − p 0 )

6Vµ

0 x 2

1 − e −α (p − p 0 )=

6Vµ 0α

(a 2 − x 2 )

h 3

e −α (p − p 0 )= 1 −

6Vµ 0α

(a 2 − x 2 )

h 3

6Vµ 0α

− α (p − p 0 )

= ln

−

(a 2 − x

2 )

159

6Vµ

0α

(

−

− x

p =

h 3

)

+ p 0 .

(16.36)

− α

Так как во втором решении присутствует ln, то начальные условия подходят не

любые, а удовлетворяющие неравенству: 0 <	6V µ	0	α	(a 2	− x 2	) < 1 . Если α → 0,
	h 3

то решение (16.36) → (16.5).

Отсутствие решения в некоторой зоне можно объяснить нарушением сплошности потока для рассматриваемой модели жидкости. Можно отметить, что для получения надежной смазочной пленки часто применяют особые добавки к жидкостям, существенно меняющим их реологические характеристики.

16.6. Течение в зазорах с облитерацией

16.6.1. Основные сведения

Явление облитерации заключается в том, что при течении вязкой жидкости под давлением через узкие щели (порядка нескольких микрометров) со временем эта щель сужается, и расход жидкости уменьшается, иногда прекращаясь полностью. Характерные времена процесса составляют несколько тысяч секунд.

Прекращение течения жидкости может вызываться двумя причинами. Первая из них сводится к наличию содержащихся в жидкости частиц грязи размеров порядка тех же микрометров. Эти частицы постепенно полностью забивают отверстие. Эта причина устраняется при очистке жидкости от грязевых частичек.

Вторая причина не устраняется фильтрами. В жидкости для улучшения различных необходимых свойств вводится поверхностно – активные вещества (ПАВ), состоящие из полярно-активных молекул. В процессе протечки жидкости через щели происходит адсорбция этих молекул на внутренней поверхности щели. Адсорбция является многослойной, так что щели также постепенно сужаются и, наконец, полностью закрываются, и расход жидкости прекращается[14].

Адсорбция молекул ПАВ является физической, т.е. обусловлена силами притяжения Ван дер Ваальса. При этом можно говорить о двух механизмах адсорбции молекул ПАВ на стенках щели.

Г.А.Никитин [14] предлагает механизм, при котором молекула ПАВ притягивается к стенке силами, вызывающими адсорбцию. Это может быть сила притяжения со стороны электрического изображения внутри металла стенки молекулы. ПАВ являются полярными молекулами, т.е. имеют статические дипольные электрические моменты, и они притягиваются к таким же дипольным моментам в изображении внутри металла стенки. Впрочем, это может быть также притяжение со стороны молекул стенки, вызванное Ван дер Ваалсовыми силами между данной молекулой ПАВ и молекулами стенки вблизи ее поверхности. В любом случае при многих слоях молекул ПАВ сила притяжения постепенно ослабевает, так как расстояние от данной молекулы ПАВ до стенки увеличивается в процессе облитерации. Если щель достаточно широкая, то облитерация является частичной, т.е. налипший слой молекул ПАВ имеет вполне определенную толщину, больше которой силы притяжения ничтожно малы. Недостатком такого механизма является факт, что силы притяжения являются весьма короткодействующими – их радиус порядка нескольких радиусов молекул. Следовательно, по такой версии слой молекул ПАВ

160

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2016 17 18 19 20 > Следующая >>>

Соседние файлы в предмете Гидравлика и гидропривод

#
02.05.2014748.46 Кб67Пневматические элементы и узлы в устройствах контроля состава и свойств веществ.pdf
#
02.05.2014434.18 Кб137Подлипенский В.С. Гидропневмоавтоматика.doc
#
02.05.20148.39 Mб126РГР - Расчёт водоснабжения посёлка и расчёт насосной установки.doc
#
02.05.2014382.31 Кб272РГР - Расчет гидропривода.pdf
#
02.05.2014107.52 Кб953Реферат - Насосы.doc
#
02.05.20144.79 Mб1018Шейпак А.А. Гидравлика и гидропневмопривод (часть 1).pdf
#
02.05.201412.36 Mб2373Шейпак А.А. Гидравлика и гидропневмопривод (часть 2).pdf
#
02.05.2014935.94 Кб365Шпоры по гидравлике.doc