Шейпак А.А. Гидравлика и гидропневмопривод (часть 1)

не может стоять больше, чем из трех-четырех мономерных слоев ПАВ. В действительности таких слоев оказывается многие десятки – ведь на толщине щели в несколько микрометров укладывается до тысячи молекул ПАВ.

В предлагаемом нами механизме молекулы ПАВ лишь с начала притягиваются стенкой щели посредством указанных короткодействующих сил Ван дер Ваалса. При наложении нескольких мономолекулярных слоев молекул ПАВ друг на друга у поверхности стенки основным становится притяжение молекул ПАВ из жидкости к уже налипшим молекулам ПАВ вблизи стенки и т.д. Все время прилипание идет с небольшой толщины жидкости вблизи границы нароста. Притяжение молекул ПАВ друг к другу вызвано также силами Ван дер Ваальса. При таком механизме зарастание щели имеет место при любой ее толщине, однако, при большой толщине время зарастания становится столь большим, что с практической точки зрения можно говорить, что его просто нет. Кроме того, при больших временах становятся существенными процессы развала нароста благодаря естественным флуктуациям.

Ниже рассмотрена реализация второго механизма облитерации щелей при течении жидкостей, содержащих ПАВ. Получен закон зарастания щелей со временем в зависимости от многочисленных физических параметров, характеризующих задачу. Показано, как разрушается облитерация при колебательном движении стенок щели.

16.6.2. Механизм облитерации

Рассмотрим явление облитерации как многослойную адсорбцию молекул ПАВ на внутренние стенки щели, через которую протекает жидкость, содержащая небольшую концентрацию ПАВ. Эта концентрация столь мала, что данный процесс является весьма медленным на фоне протекания жидкости через щель.

Обратимся сначала к вопросу о силе, с которой молекула ПАВ притягивается к многослойному наросту из молекул ПАВ на стенке щели. Сначала, когда нарост отсутствует, молекула ПАВ адсорбируется на внутренней поверхности стенки вследствие ее притяжения к молекулам, из которых состоит стенка. Однако большую часть времени в процессе облитерации молекула ПАВ притягивается к наросту из таких же молекул, слипшихся друг с другом практически вплотную: эта сила притяжения значительно больше, чем взаимодействие молекулы ПАВ из потока жидкости со стенкой щели.

Молекула ПАВ обладает статическим дипольным моментом, так что потенциальная энергия электрического взаимодействия двух молекул ПАВ друг с другом имеет вид

ский момент этих взаимодействующих молекул, n − единичный вектор вдоль прямой, соединяющей молекулы.

Конечно, направления векторов дипольных моментов p1 и p2 могут быть произвольным. Из (16.37) видно, что при усреднении по направлениям p1 и p2 по-

161

тенциальная энергия обращается в нуль. Это означает, что в первом порядке теории возмущений молекулы не взаимодействуют друг с другом. Во втором порядке по V12 энергия потенциального взаимодействия U12 молекул друг с другом убыва-

ет как r −6 и представляет собой Ван дер Ваальсов потенциал. Ван дер Ваальсово притяжение справедливо только при больших расстояниях между молекулами. На малых расстояниях оно сменяется резким отталкиванием, явный вид которого обычно подбирается феноменологически. Наиболее распространен потенциал Лен-

нарда – Джонса, в котором отталкивание зависит от расстояния как r −12 . Сам потенциал записывается в виде:

Константы ε и σ в этой зависимости подбираются феноменологически для каждого сорта взаимодействия молекул. Типичные значения этих констант для углеводородов и других органических молекул составляют εk = 400K ( k − постоянная

Мы полагаем, что облитерация вызвана дальнодействующей притягивающей компонентой взаимодействия (16.38), т.е. силами Ван дер Ваальса. Итак, для потенциальной энергии взаимодействия молекул ПАВ друг с другом берем выражение:

Это выражение определяет потенциальную энергию взаимодействия молекулы ПАВ в жидкости с одной молекулой ПАВ в слое нароста на стенке. Для нахождения полной энергии взаимодействия данной молекулы ПАВ со всей стенкой нужно просуммировать выражение (16.39) по всем молекулам нароста. Пусть V − характерный объем, занимаемый одной молекулой ПАВ в наросте. Тогда 1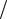V −

число молекул ПАВ в единице объема нароста. Производим интегрирование (16.39) по молекулам нароста в цилиндрической системе координат:

Здесь z0 − кратчайшее расстояние от данной молекулы ПАВ до плоскости

нароста (рис. 60), z − координата вдоль направления z , перпендикулярного плоскости нароста.

Производя интегрирование (16.40), находим:

Дифференцируя это выражение по z0 , находим силу притяжения молекулы ПАВ к наросту:

162

где константа α = 2πσ 6 ε /V .

°

Пусть ε / k = 400K,σ = 5 A,V = a3 , где a − характерный размер молекул ПАВ.

°

Возьмем в качестве примера a = 2 A . Тогдаα = 6,8 10−47 H ì 4 .Несложно вычислить

эту константу и для других значений параметров (порядок ее величины остается тем же).

Рассмотрим плоскую прямоугольную щель с малым начальным зазором h и большой шириной. На рис. 60 показано поперечное сечение щели (вид спереди). Поток жидкости идет перпендикулярно плоскости листа бумаги. Толщину нароста в данный момент времени t обозначим S(t) . Молекула ПАВ находится в точке А

на рис. 60.

S(t)

z

у

h h` А

z0

Рис. 60. Вид щели спереди. Нарост из молекул ПАВ заштрихован, z0 −расстояние от данной молекулы ПАВ до нароста

Сила F уравновешивается силой трения Стокса

(16.43)

При этом мы считаем молекулы ПАВ сферическими телами диаметра a . Характерный размер a уже вводился выше. Величина µ − коэффициент динамической вязкости жидкости. Например, для машинного масла при комнатной температуре имеем µ = 0,1Ïà ñ . Величина Vz представляет собой скорость молекулы ПАВ

Уравнение движения имеет вид Fc = F . Что касается инерционного члена mV&z , где m − масса молекулы ПАВ, то им можно пренебречь вследствие малости этой массы и считать, что молекула движется к наросту безынерционно. Из (16.42) и (16.43) получаем выражение для скорости Vz молекулы ПАВ в зависимости от ее расстояния z от нароста :

z04

Здесь обозначено

163

(16.44) следует, что, например, при z0 =10a , скорость Vz движения молекулы ПАВ

к наросту составляет 2.2 ñì / ñ .

Мы видим, что сила притяжения молекулы ПАВ к наросту является весьма короткодействующей: она быстро убывает, когда расстояние до нароста велико по сравнению с размером молекулы ПАВ. Таким образом, при данном наросте основной вклад в дальнейшем налипании молекул ПАВ вносят молекулы, расположенные вблизи поверхности нароста при входе в отверстие щели.

Теперь обратимся к движению жидкости вдоль направления щели. Скорость Vx вдоль щели шириной h′ = h − 2s при вязком ламинарном течении имеет вид (на

Здесь dp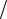dx – градиент давления в щели. Будем считать его равным вдоль всей щели, так что

представляет собой текущий зазор щели, υx − скорость одной стенки относительно другой, если она существует.

16.6.3. Уравнение траектории молекул

Дифференциальное уравнение траектории молекулы ПАВ имеет следующий

вид:

Эта траектория показана на рис. 61 сплошной линией для случая, когда молекула ПАВ прилипает к правому краю щели. При меньших значениях z0 молекула ПАВ прилипает к наросту, при больших пролетает щель, не прилипая.

164

S(t)

z

x

h h`

z0

L

Рис. 61. Вид щели сбоку, зона облитерации в щели заштрихована, как на рис. 60

Подставляя (16.44) и (16.45,а) в (16.47), находим:

Отметим, что перемещение молекулы ПАВ вдоль щели происходит за время порядка LVx , т.е. например, при L =1 см за времена порядка 10−2 с. Эти времена

малы по сравнению с временем образования характерного нароста на щели, которое происходит за минуты и более. Поэтому время t , от которого зависит эффективная ширина щели h′, можно считать (в 16.48) не переменной величиной, а заданным параметром: за время движения определенной молекулы ПАВ щель не успевает заметным образом сузиться. То же относится к медленной функции υx, если таковая зависимость имеется. Интегрирование (16.48) по граничной траектории, показанной на рис.61, приводит к следующему результату:

Уравнение (16.49) связывает две неизвестные величины: z0 и h′, нужно еще одно уравнение для этих величин.

165

16.6.4.Закон сохранения числа молекул

Всоответствии с рис.61 все молекулы ПАВ с координатой менее z0 попада-

ют на нарост в щели и увеличивают толщину этого нароста s. Обозначим через N концентрацию ПАВ в жидкости, т.е. число молекул ПАВ в единице объема жидкости. Величина NV определяет плотность потока молекул ПАВ. Число молекул ПАВ, проходящих через единицу ширины щели за 1 с, равно

z∫0 NVx dz .

0

Все эти молекулы оседают на нижней половине щели, распределяясь равномерно вдоль длины щели L , так как в рассматриваемой задаче нет зависимости физических величин от координаты x вдоль щели. Значение z = 0 в нижнем пределе интеграла соответствует границе между жидкостью и наростом. Деля этот интеграл на L и умножая на объем υ одной молекулы ПАВ(υ = a3 , где a – характер-

ный размер этой молекулы), получим увеличение толщины нароста s за 1 с, т.е. dsdt . Итак, находим:

16.6.5. Облитерация в щели с неподвижной стенкой

При υx = 0 из (16.49) и (16.51) получаем систему из двух уравнений:

Перейдем к безразмерным переменным:

166

Тогда система (16.53) в новых переменных запишется следующим образом:

Мы видим, что в безразмерную систему уравнений входит одна безразмерная константа δ . Для рассмотренного выше численного примера β = 3.6 10−37 ì 5 / ñ ,

µ = 0,1 Ïà ñ, L =1 ñì , ∆p = 2 ÌÏà , и h =10 ìêì получаем: δ = 3.6 10−13 <<1. Это

означает, что всегда U << H ,т.е. на каждом этапе облитерация происходит от молекул вблизи поверхности нароста. Следовательно, с большой степенью точности можно упростить систему(16.55):

Мы видим, что время зарастания щели растет с увеличением толщины щели h и её длины L . Увеличение перепада давления уменьшает время зарастания, так как больший расход жидкости приводит к большему выпадению молекул ПАВ в нарост.

Проведем численные оценки времени зарастания t0 , взяв из приведенного выше примера значение β = 3,6 10−37 ì 5 / ñ , µ = 0,1 Ïà ñ, L =1 см, ∆p = 2 МПа и h =10 мкм. Величина Nυ представляет собой относительную объемную долю ПАВ в жидкости, примем ее равной 10-2. Получаем: t0 =106 c , т.е. облитерация практически не происходит. При L =1 мм имеем t0 = 3 104 c .

167

В случае очень сильного встряхивания система (16.62) упрощается:

Исключая U из системы, находим уравнение для H :

Так как δ <<1, то решение (16.68) представляет собой очень слабую осцилляцию на фоне невозмущенного решения, соответствующего отсутствию облитерации.

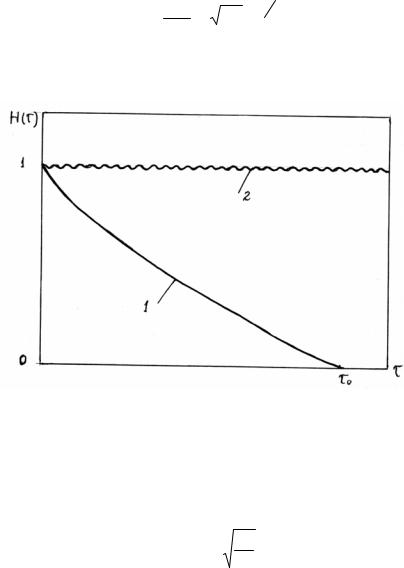
Рис. 62. Облитерация: 1 – в отсутствии движения стенок, 2 – при сильном встряхивании стенки

Система(16.62) легко решается численно на ЭВМ. Для этого на каждом шаге интегрирования дифференциального уравнения (применялся метод Эйлера) необходимо решать каким-либо методом (применялся метод простой итерации) алгебраическое уравнение шестой степени.

Первое приближение для U подсчитывается по формуле:

U1 = 6 6Hδ .

169

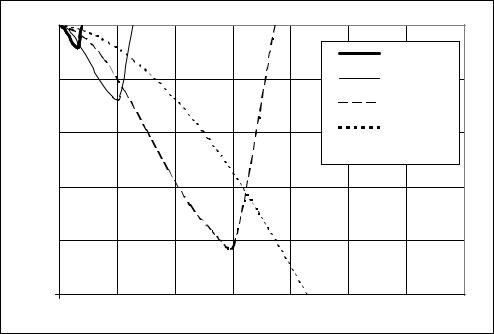
Рис. 63. Влияние колебательного влияния стенки на механизм облитерации

На рис. 63 представлен результат численного исследования явления облитерации при синусоидальном законе движения стенки щели. При повышении частоты облитерация разрушается.

16.7. Щелевое уплотнение со стохастической геометрией

Надежность работы гидромашин и гидропневмоарматуры в значительной мере определяется качеством подвижных и неподвижных уплотнений. Создание адекватных гидромеханических моделей таких устройств поэтому является важной задачей. Рассмотрим одну из частных задач: течение вязкой несжимаемой жидкости через нормально негерметичное неподвижное уплотнение. Расстояние между поверхностями принимается случайным и описывается функцией с нормальным распределением h=f(x, y).

Решение гидромеханической задачи находится в приближении теории смазочного слоя в форме, полученной Осборном Рейнольдсом. Область течения задается следующим образом: по оси x – [0 a], по оси y – [0, b], по оси z – [0, h(x, y)]. Математическая модель сводится к дифференциальному уравнению в частных производных эллиптического типа для поля давлений:

При нахождении решения сначала генерируется равномерно распределенная величина, затем по ней – нормально распределенная со следующими параметрами: максимальное h(max) и минимальное значение зазора h(min); математическое ожидание принимается равным среднему арифметическому значению зазора, а среднее квадратическое – 1/6 от размаха. Решение уравнения для давления проводилось ме-

170