Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Гидравлика и гидропривод

Файл:

Шейпак А.А. Гидравлика и гидропневмопривод (часть 1)

.pdf

Скачиваний:

1018

Добавлен:

02.05.2014

Размер:

4.79 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 206 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Производя интегрирование, можно получить среднее значение касательного турбулентного напряжения:

		1 t+T		′ ′
	′				′ ′
		T	∫t
τxy =						,	(5.32)
			− ρVyVx dt = −ρVyVx

где Vy′Vx′ – среднее произведение пульсации скоростей.

Аналогичные выкладки можно проделать для всех составляющих напряжений поверхностных сил.

Таким образом, в турбулентном потоке (кроме вязкостных поверхностных сил) надо учитывать дополнительные – турбулентные, обусловленные наличием пульсаций. Уравнение движения примет тогда следующий вид:

′2

′

∂Vx

∂V

∂Vx +V

∂Vx

= F −

∂ p

+ν∆V

−

+ ∂VxVz

∂t

∂x

∂y

∂z

ρ ∂x

∂x

∂y

∂z

′2

∂Vy

′

∂Vy

′

1 ∂ p

∂VxVy

∂VyVz

+Vx

+Vy

+Vz

= Fy −

+ν∆Vy −

(5.33)

∂t

∂x

∂y

∂z

ρ ∂y

∂x

∂y

∂z

′2

′

′ ′

∂Vz

+Vx

∂Vz

+Vy

∂Vz

+Vz

∂Vz

= Fz

−

1 ∂ p

+ν∆Vz −

∂VxVz

∂Vz

∂t

∂x

∂y

∂z

ρ ∂z

∂x

∂y

∂z

Система (5.33) носит название уравнений Рейнольдса.

Отметим, что уравнение неразрывности для турбулентного движения имеет такой же вид в силу своей линейности, как и для ламинарного режима течения. Уравнения Рейнольдса можно получить из уравнений Навье-Стокса, производя осреднение по времени.

Уравнения Рейнольдса образуют незамкнутую систему. Задача замыкания имеет много решений, но ни одно из них не является в настоящее время исчерпывающим проблему. Одной из первых гипотез, предложенных Буссинеском, являлась гипотеза кажущейся турбулентной вязкости:

	µэфф = µ + µт, τт = µт	∂	V	,	(5.34)
	µэфф = µ + µт, τт = µт	∂n		,	(5.34)
где µ – вязкость жидкости;		∂n
где µ – вязкость жидкости;
µт	– турбулентная вязкость;
µэфф	– эффективная вязкость.

Турбулентная вязкость не является свойством жидкости, а определяется кинематическими характеристиками турбулентного течения и его предысторий. В настоящее время имеется множество полуэмпирических теорий для определений кажущейся турбулентной вязкости. При таком подходе в вычисленном плане задачи для ламинарного и турбулентного режимов течения становятся идентичными, но при турбулентном течении появляется блок (и соответствующая подпрограмма) для вычисления кажущейся вязкости. Величина турбулентной вязкости может на несколько порядков превышать величину физической вязкости. Это дало основание Ричардсону сказать крылатую фразу о том, что турбулентная вязкость воды равна вязкости ламинарного меда.

Порядок величины вязкого касательного напряжения в соответствии с формулой Ньютона будет

τη = µ Vd .

Вычислим отношение

τò = ρVx′V ′y . τν µV

Если Vx′ = Vy′ ≈ 0.1V , тогда

τ	т	=	0.01ρV 2d	= 0.01Re.		(5.35)
			µV
τν
Таким образом, если Re = 104, то τт τν					= 100. Следовательно, турбулентная

вязкость может быть на несколько порядков больше ламинарной.

6. АБСОЛЮТНЫЙ И ОТНОСИТЕЛЬНЫЙ ПОКОЙ (РАВНОВЕСИЕ) ЖИДКИХ СРЕД

Состояние жидкости, при котором скорости всех ее точек в любой момент времени равны нулю, называется (механическим) равновесием в данной системе отсчета. Если любой выделенный объем жидкости находится в равновесии, то поверхностные силы действуют лишь перпендикулярно элементарным поверхностям. Существование касательных составляющих поверхностных сил при равновесии невозможно, так как из-за текучести любая сколь угодно малая сила вызовет деформацию жидкости, т.е. нарушит механическое равновесие системы.

6.1. Основной закон гидростатики

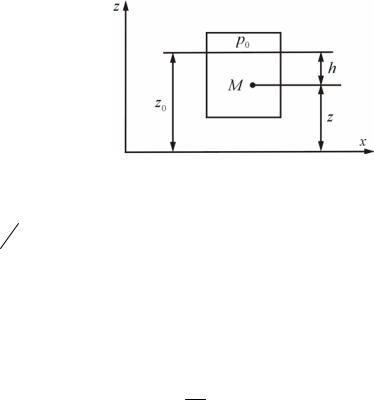
Рассмотрим равновесие несжимаемой жидкости в неподвижном сосуде, находящемся в равномерном (параллельном) поле сил тяжести (рис. 18).

Рис. 18. Абсолютный покой жидкости в равномерном поле сил тяжести

	Тогда при соответствующем				выборе системы координат	Fx = Fy = 0 и
F	= −g = −∂Φ	∂z	.
x		∂z
	Очевидно, что Φ = gz + C , где C – произвольная постоянная.
	Принимая во внимание (4.3), получим
			z +	p	= const	(6.1)
			z +	ρg	= const	(6.1)
				ρg

Для нахождения постоянной С используем условие p=p0 при z=z0, где p0 – давление на свободной поверхности (граница газ-жидкость).

z0 + ρp = C. g

Тогда

p = p0 + ρg(z0 − z) = p0 + ρgh,

(6.2)

где h = z0 − z .

Величина ρgh называется весовым давлением. Из основного закона гидроста-

тики следуют известные из школьного курса физики закон Паскаля и закон сообщающихся сосудов.

6.2. Закон Архимеда

Для определения поверхностных сил, действующих со стороны неподвижной жидкости на тела, погруженные в нее и покоящиеся относительно жидкости, необходимо найти сумму элементарных сил давления F = pi∆Ai, действующих на поверхность тела. Метод подсчета такой суммы основан на независимости поверхностных сил от вещества, из которого состоит тело. Это позволяет мысленно заменить погруженное твердое тело жидким телом такой же формы и размера, состоящим из той же жидкости, что и остальной объем. Поверхностные силы при такой замене не изменятся, а условие равновесия погруженного жидкого тела массы т под действием поверхностных сил и силы тяжести, приложенной к центру масс жидкого тела, очевидно:

F=-mg

(6.3)

Сумма поверхностных сил, действующих на тело, покоящееся в неподвижной жидкости, равна по величине и противоположна по направлению весу жидкости, вытесненной телом, и приложена к центру масс вытесненной жидкости. Это утверждение называется законом Архимеда, а суммарная поверхностная сила - вы-

талкивающей силой или силой Архимеда.

Тела, которые тяжелее жидкости, будучи опущены в жидкость, погружаются все глубже и глубже, пока не достигают дна, и, пребывая в жидкости, теряют в своем весе столько, сколько весит жидкость, взятая в объеме этих тел. В случае неоднородного поля тяжести или действия других сил точку приложения выталкивающей силы (бароцентр) можно найти из условий равновесия жидкости

6.3.Равновесие жидкости в сосуде, движущемся прямолинейно

спостоянным ускорением

Равновесие при условии движения сосуда с ускорением называется относи-

тельным покоем.

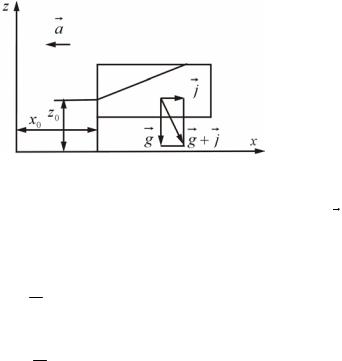
Рис. 19. Относительный покой в сосуде, движущемся с постоянным ускорением

При прямолинейном движении сосуда с постоянным ускорением a (рис. 19)

Fx = −a = j,

Fy = 0,

Fz = −g.

Используя уравнение (5.5), получим

ρ1 dp = jdx − gdz.

Интегрируя, найдем

ρp = jx − gz + C.

Если принять p = c o n s t , то получим уравнение поверхностей уровня (изобарических поверхностей):

jx − gz + C1 = 0,

которые являются плоскостями, параллельными оси Y и нормальными сумме векторов j и g:

C1 = gz0 − jx.

Тогда распределение давлений определяется формулой

p = p0 + ρj(x − x0 ) + ρg(z0 − z).

(6.4)

6.4. Сила давления жидкости на плоскую стенку. Центр давления

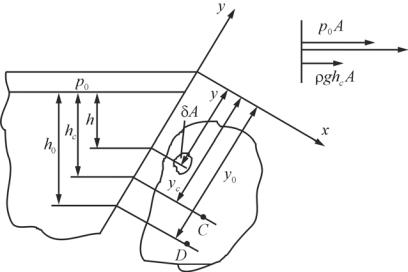
Подсчитаем силу давления жидкости на элемент плоской стенки площадью A. Стенка наклонена к горизонту под плоским углом α (рис. 20).

Рис. 20. Сила давления, действующая на плоскую стенку

Давление на свободной поверхности p0 . Элементарная сила давления будет:

dP = pdA = ( p0 + ρgh)dA = p0 dA + ρghdA.

Полная сила давления определяется по площади

P = p0 ∫dA +ρg ∫hdA =p0 A + ρg sinα ∫ ydA,

A	A	A
где ∫ ydA = yc A – статический момент площади относительно оси X,
A
c – координата центра масс плоской фигуры.
Таким образом,	P = ( p0 + ρghc )dA = pc A.
	P = ( p0 + ρghc )dA = pc A.	(6.5)

Полная сила давления жидкости на плоскую стенку равна произведению площади стенки на величину гидростатического давления в центре масс плоской фигу-

ры. В машиностроении обычно p0 >> ρghc и P = p0 A .

(6.6)

Для вычисления центра давления (точки приложения суммарной силы давления P) найдем сначала центр давления для силы, обусловленной весовым давлением. Используя теорему Вариньона (момент равнодействующей силы давления относительно оси Х равен сумме моментов составляющих сил) и теорему Штейнера о

связи моментов инерции относительно параллельных осей, можно получить координату приложения суммарной силы весового давления (центр давления).

yD = yc +	Jc	,	(6.7)
	yc A

т.е. центр давления расположен ниже центра масс плоской площадки. Сила давления p0 A , очевидно, приложена в центре масс – точке С. Центр давления равнодей-

ствующей силы P = p0 A + ρghc A находится между точками С и D. Однако в гидротехнике, когда p0 = pa (атмосферное давление), положение центра давления опре-

деляется только весовым давлением, и различие между точками С и D становится определяющим.

6.5. Задачи

6.5.1.

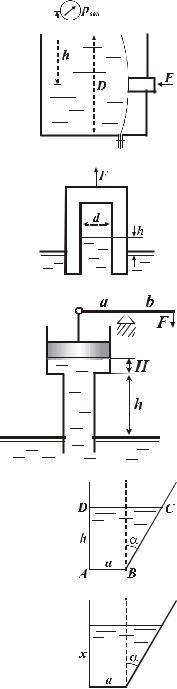
Определить силу F, действующую на шток гибкой диафраг-

мы, если ее диаметр D=200 мм, показание вакуумметра pвак=0,05 МПа, высота h=1 м. Площадью штока пренебречь. Жидкость – вода.

6.5.2.

Определить высоту h, если поддерживающая сила F=10 H. Вес сосуда G=2 H, его диаметр d=60 мм. Толщиной стенки сосуда пренебречь. Жидкость вода.

6.5.3.

Определить силу F, необходимую для удержания в равновесии поршня, если труба под поршнем заполнена водой, а размеры трубы: D = 100 мм, H = 0,5 м, h = 4 м. Длины рычага: a = 0,2 м, b = 1,0 м. Собственным весом поршня пренебречь.

6.5.4.

При каком угле α момент, действующий на подвижную стенку, будет минимален? Количество воды в баке не меняется. При α=0 высота воды в баке равна ширине дна бака.

6.5.6.

При каком угле α момент, действующий на подвижную стенку, будет минимален? Количество воды в баке не меняется.

6.5.7.
	При каком угле α момент, действующий на подвижную стен-
ку, будет минимален? Количество воды в баке не меняется.
6.5.8.
	Палочка одним концом шарнирно закреплена в точке 0, а
другим погружена в воду. Палочка может вращаться относи-
тельно горизонтальной оси шарнира, находящегося над уров-
нем жидкости. Найти плотность ρn материала палочки, если
при равновесии в воду погружена её половина. Вычислить
отношение силы реакции R в шарнире 0 к весу палочки Р.
6.5.9.
	Кусок льда объемом V=2 дм3 плавает в цилиндрическом со-
суде с площадью основания S=2 дм2, заполненном водой и
				_		= ρл	= 0,9 ; масла
маслом. Относительная плотность льда ρ					л
						ρ
						воды
_		=	ρм	= 0,8. Как изменятся уровни H,h в сосуде, когда лед
ρ	м
			ρводы
растает?
6.5.10.
Топливный бак самолета заполнен на 1/3 его емкости. Само-
лет движется горизонтально с постоянным ускорением a. Оп-
ределить ускорение a, при котором свободная поверхность
проходит через точку A, что будет соответствовать прекра-
щению подачи бензина из бака.

6.5.11.

Закрытый цилиндр высотой H=0,1 м и радиусом R=0,2 м наполнен на три четверти водой. С какой угловой скоростью ω должен вращаться цилиндр вокруг его вертикальной 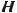оси, чтобы свободная поверхность коснулась дна? Объем параболоида равен половине объема цилиндра с такими же высотой и радиусом.

6.5.12.

Определить минимальную частоту вращения n, которую 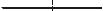нужно сообщить сосуду вокруг его вертикальной оси для пол- ного его опорожнения. Размеры: D=460 мм, d=200 мм, H=75 мм.

7.МОДЕЛЬ ИДЕАЛЬНОЙ (НЕВЯЗКОЙ) ЖИДКОСТИ

7.1.Уравнение движения идеальной жидкости в форме Эйлера

Полагая в уравнениях движения (5.1) и (5.2) касательные напряжения равными нулю и учитывая, что в этом случае:

pxx = pyy = pzz = −p,

получим дифференциальные уравнения движения идеальной жидкости в форме Эйлера в проекциях:

dVx

dt dVy

dt dVz

или в векторной форме:

= Fx − ρ1 ∂∂px ,

= Fy −	1 ∂p	,	(7.1)

	ρ ∂y

=Fz − 1 ∂p

ρ∂z

= F −

grad p.

(7.2)

В случае несжимаемой жидкости система (7.1) вместе с уравнением неразрыв-

ности

∂Vy

∂V

= 0

(7.3)

∂y

∂x

∂z

является замкнутой.

Решением системы будут функции

p = f1 (x, y, z,t),

Vx = f2 (x, y, z,t),

Vy = f3 (x, y, z,t),

Vz = f4 (x, y, z,t),

определяющие векторное поле скорости и скалярное поле давлений для каждого момента времени.

Для нахождения зависимости координат жидкой частицы от времени t и начального положения (координаты x0 , y0 , z0 ) необходимо проинтегрировать еще од-

ну систему из трех уравнений:

dx	= f2 (x, y, z,t),	dy	= f3 (x, y, z,t),	dz	= f4 (x, y, z,t).	(7.4)
dt		dt		dt

В случае сжимаемой жидкости плотность в общем случае является функцией давления и температуры (часто вводят понятие невязкого и нетеплопроводного газа). Для исследования движения жидкости в этом случае необходимо привлечь еще уравнение энергии. В нашем курсе мы ограничимся частным случаем движения сжимаемой жидкости, когда плотность является функцией, зависящей только от давления. Такие жидкости называются баротропными и для них система (7.2) – (7.3) является замкнутой. Для баротропной жидкости целесообразно ввести функцию давления P (x,y,z), определяемую как:

dP =	dp	=	dp	.	(7.5)
	ρ		ρ( p)

Величина dP является полным дифференциалом, поэтому

1 ∂p

ρ ∂x

ρ ∂y

ρ ∂z

(7.6)

grad P = ρ1 grad p.

Для нахождения частных решений дифференциальных уравнений гидродинамики необходимо задать начальные и граничные условия. Начальные условия состоят в нашем случае в задании поля скоростей в начальный момент времени.

Vx (x, y, z,t0 ) Vy (x, y, z,t0 ) Vz (x, y, z,t0 )

= ϕ1 (x, y, z),

= ϕ2 (x, y, z), (7.7) = ϕ3 (x, y, z).

В зависимости от конкретной задачи граничные условия могут быть разными. Рассматривая движение жидкости в области с подвижными поверхностями (например, поршневой насос или цилиндр двигателя внутреннего сгорания), допустим, что жидкость прилегает к стенке, но не протекает через нее. Проскальзывание частиц идеальной жидкости относительно стенок допустимо. В рассматриваемом случае граничное условие будет, очевидно, состоять в том, что скорость перемещения любой точки поверхности и скорость прилегающей к ней частицы жидкости

должны иметь одинаковые проекции на нормаль к поверхности. Если уравнение поверхности будет

F(x, y, z,t) = 0,

(7.8)

то, дифференцируя неявную функцию по t, получим искомое граничное условие:

∂F	Vx +	∂F	Vy +	∂F	Vz +	∂F	= 0 .	(7.9)
						∂t
∂x		∂y		∂z

Следует отметить, что аналитических решений уравнений движения идеальной жидкости известно немного. Численное же решение системы (7.1) ненамного проще, чем решение системы уравнений для вязкой жидкости, более адекватно описывающих реальные процессы. Однако анализ уравнений движения идеальной жидкости позволяет получить целый ряд очень важных для теории и практики результатов.

7.2. Уравнение идеальной жидкости в форме Громека – Ламба

Используя известное из векторного анализа преобразование

12 grad V 2 = (V )V + [V ×rot V ],

уравнение движения в форме Эйлера можно переписать в следующем виде:

∂V	+ grad	V 2	− [V ×rot V ]= F −	1	grad p.	(7.9,а)
∂t		2		ρ

(7.9,а) – уравнение движения идеальной жидкости в форме Громека – Ламба. Отметим, что русский ученый И.С. Громека и англичанин Ламб получили подобную форму записи в виде проекций на оси координат.

Очевидно, что V 2 =Vx 2 +Vy 2 +Vz 2 = (V V ). Уравнение (7.9,а) является преобразованием уравнения Эйлера и по существу не отличается от него. Допустим далее

баротропность жидкости и существование потенциала массовых сил F = −grad Φ. Тогда уравнение (7.9,а) примет следующий вид:

∂V				V	2	= [V ×rot V ],
		Φ +P	+				(7.10)

∂t	+ grad			2

где P = ∫ dpρ .

7.3. Интегралы уравнений движения идеальной жидкости

7.3.1. Установившееся безвихревое движение

Рассмотрим уравнение движения в форме Громека – Ламба для баротропной жидкости в поле массовых сил, имеющих потенциал. Так как по условию ∂V ∂t = 0 и rot V = 0, то из (7.10) следует

					V	2
	Φ +P		+		V		= 0

grad					2
					2
или
Φ +P +		V 2		= const.				(7.11)
Φ +P +				= const.				(7.11)
	2

Это равенство называется интегралом Бернулли и выполняется для всей области пространства, заполненного жидкостью с потенциалом скорости. Если жидкость несжимаемая, а массовые силы представлены только равномерным полем сил тяготения, то

P =	p	и	Φ = gz.
	ρ

и из (7.11) следует

gz +

V 2

= const .

(7.12)

7.3.2. Установившееся вихревое движение

Так как в этом случае ∂V

∂t

= 0, то

[V ×rot V

]..

Φ +P

grad

Возьмем произвольно направленный отрезок dl

и умножим скалярно на него

обе части полученного уравнения:

→

( dl ) gradΦ +P +

×rotV

dl .

Очевидно, что если dl совпадает по направлению с линией тока или вихревой линией, имеет место следующее равенство:

grad Φ +P + V22 dl = d Φ +P + V22 = 0,

или

Φ +P + V 2 = const. 2

<<< < Предыдущая 1 2 3 4 56 / 206 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете Гидравлика и гидропривод

#
02.05.2014748.46 Кб71Пневматические элементы и узлы в устройствах контроля состава и свойств веществ.pdf
#
02.05.2014434.18 Кб137Подлипенский В.С. Гидропневмоавтоматика.doc
#
02.05.20148.39 Mб128РГР - Расчёт водоснабжения посёлка и расчёт насосной установки.doc
#
02.05.2014382.31 Кб273РГР - Расчет гидропривода.pdf
#
02.05.2014107.52 Кб955Реферат - Насосы.doc
#
02.05.20144.79 Mб1018Шейпак А.А. Гидравлика и гидропневмопривод (часть 1).pdf
#
02.05.201412.36 Mб2374Шейпак А.А. Гидравлика и гидропневмопривод (часть 2).pdf
#
02.05.2014935.94 Кб365Шпоры по гидравлике.doc