3.2. Уравнение Ньютона-Рихмана. Коэффициент теплоотдачи.

Основной закон конвективного теплообмена, закон Ньютона-Рихмана, гласит:

удельный тепловой поток при конвективном теплообмене пропорционален абсолютной разности температур поверхности и жидкости (уравнение Ньютона-Рихмана)

, ,

где  - коэффициент теплоотдачи, который является важным теплофизическим параметром при описании конвективного теплообмена.

Применяя закон Фурье к пограничному слою, получим на границе поверхность - жидкость (у=0)

.

Приравнивая уравнения получим дифференциальное уравнение теплоотдачи

.

Из дифференциального уравнения теплоотдачи можно определить величину 

.

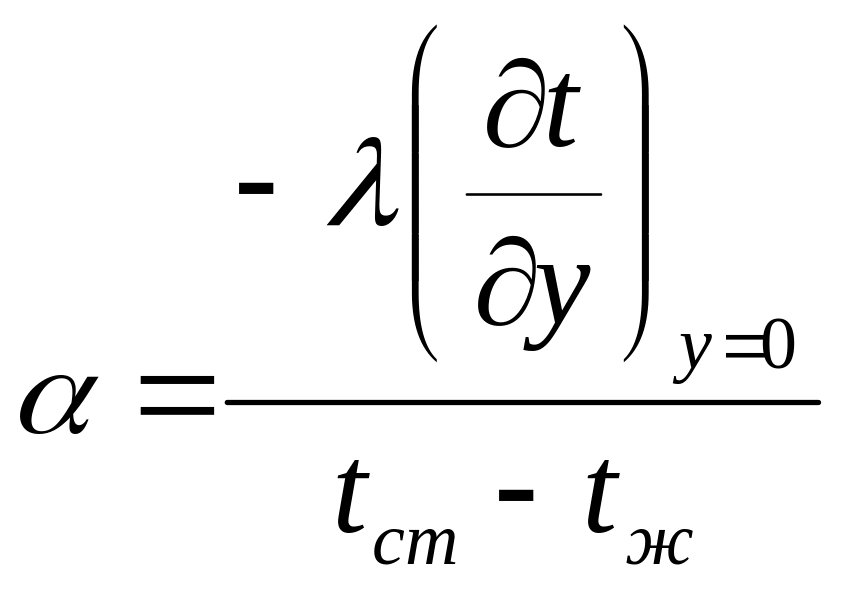Для определения  необходимо знать уравнение температурного поля в тепловом пограничном слое, что представляет математические трудности.

3.3. Дифференциальные уравнения конвективного теплообмена.

Для описания температурного поля в жидкости в условиях конвективного теплообмена используют систему из 4-х дифференциальных уравнений для конвективного теплообмена, учитывающих, как тепловые, так и гидродинамические условия протекания процесса:

1. Дифференциальное уравнение энергии, которое описывает зависимость изменения температуры в любой точке поля от времени и скорости течения жидкости. Для неподвижной среды (если скорость равна 0) это уравнение переходит в дифференциальное уравнение теплопроводности.

2. Дифференциальное уравнение конвективного теплообмена, которое выражает условия теплообмена на границе твердой поверхности и жидкости и определяет величину коэффициента теплоотдачи.

3. Дифференциальные уравнения движения вязкой несжимаемой жидкости - уравнение Навье-Стокса - по трем осям координат. Это уравнение выражает равенство проекций на каждую ось координат равнодействующей сил давления, подъемной силы и сил внутреннего трения проекциям на эти же оси сил инерции.

4. Дифференциальное уравнение сплошности (или неразрывности) потока жидкости.

Решение данной системы уравнений представляет значительные математические трудности, а в общем виде невозможно.

В отдельных случаях возможны частные решения при условии существующих упрощений и допущений.

Экспериментальное определение коэффициента теплоотдачи в каждом конкретном случае требует больших затрат, а в ряде случаев невозможно.

Для обобщения экспериментальных данных по конвективному теплообмену на возможно большое число подобных процессов и явлений теплообмена в инженерной и научной практике используются методы теории подобия.

3.4. Основные положения теории подобия для конвективного теплообмена.

Для обобщения экспериментальных данных и распространения их на многие

аналогичные процессы используется теория подобия (тория теплового моделирования), на основе которой изучение сложного и громоздкого процесса заменяется изучением простой, но подобной модели.

Теория подобия - есть учение о подобных явлениях.

Два физических процесса будут подобными если они происходят в геометрически подобных системах, а отношение одноименных параметров (линейные размеры, скорость, плотность, температура и т.д.) в сходственных точках систем есть постоянные величины, называемыми константами подобия.

Следовательно, создание подобной модели любого явления связано с соблюдением геометрического, теплового и кинематического подобия.

Из изложенного следует, что константы подобия могут быть применимы ко всем без исключения величинам характеризующим явление.

Геометрическое подобие:

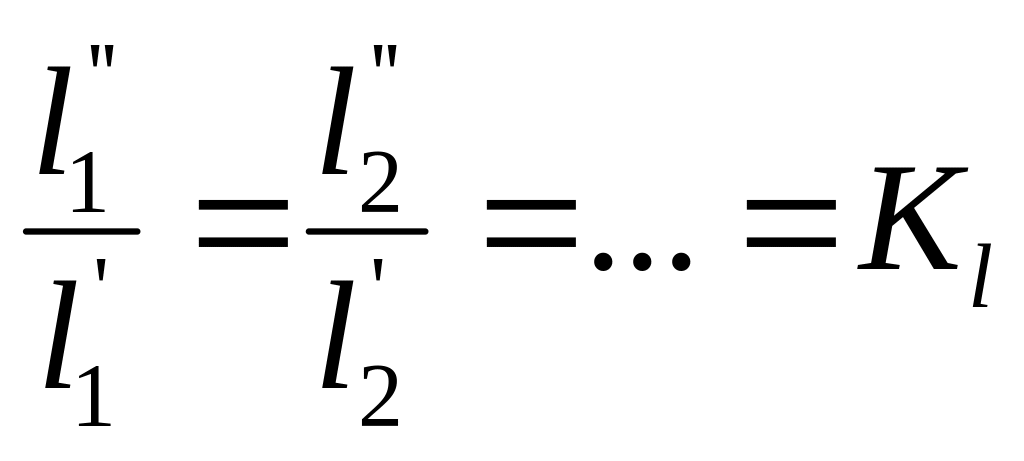- константа геометрического подобия;

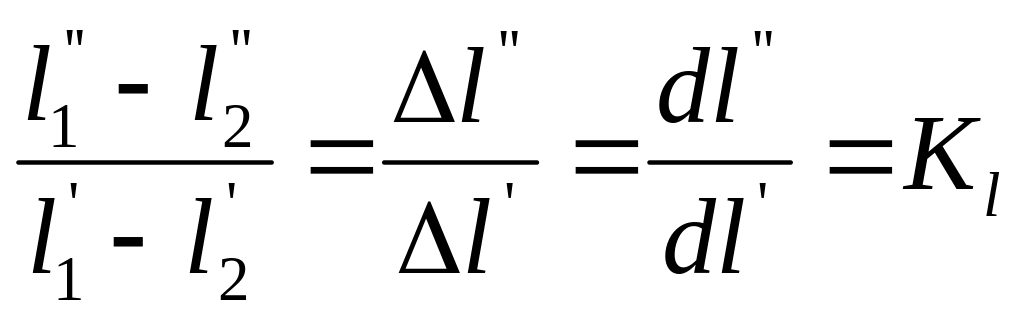- то же, но отнесенное к разности подобных величин.

Подобие температурных полей:

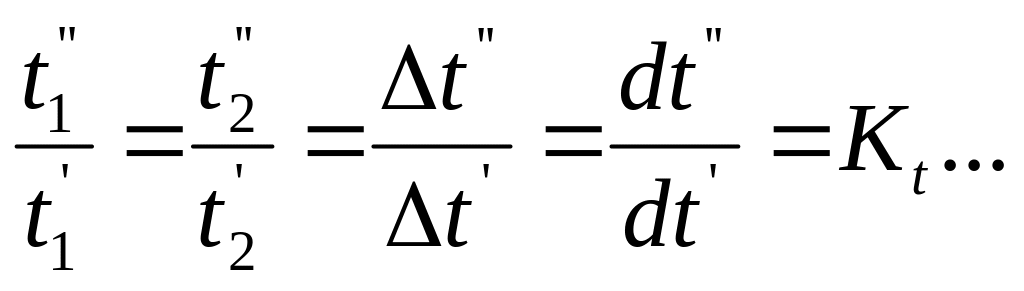- константа температурного подобия;

и т.д.

Кроме констант подобия, подобные явления характеризуются также безразмерными комплексами, составленные из величин характеризующих явление, которые у подобных явлений в сходственных точках имеют численно одинаковые значения.

Такие безразмерные комплексы в теории подобия называются числами подобия или критериями подобия.

Критерии подобия не составляются произвольно, а выводятся из аналитических зависимостей между физическими величинами, представленных в данном случае в виде системы 4-х дифференциальных уравнений конвективного теплообмена.

Критерии подобия называют по именам крупных ученых предложивших и обосновавших их применения.

Например из дифференциального уравнения теплоотдачи для двух подобных процессов следует

1). _ст ,

2). _ст .

Обозначив константы подобия

.

Подставляя во 2-е уравнение имеем

_ст .

Сравнивая с уравнением (1) имеем

откуда

Подставляя константы имеем

Полученный безразмерный комплекс называется критерием Нуссельта.

.

Физический смысл критерия Нуссельта вытекает из преобразования

,

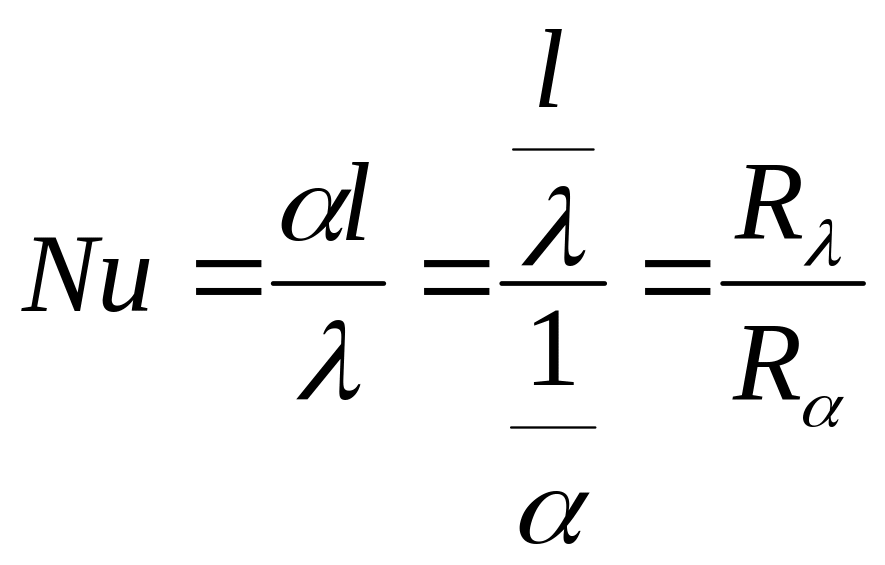т.е. критерий Нуссельта есть отношение термического сопротивления при теплопроводности для слоя жидкости толщиной l, к термическому сопротивлению теплоотдачи между жидкостью и твердой стенкой.

Аналогично, из остальных дифференциальных уравнений конвективного теплообмена, определяются другие критерии подобия, используемые для описания этого процесса.

Из дифференциального уравнения движения жидкости уравнение Навье-Стокса получены следующие критерии подобия, описывающие гидромеханическое подобие явлений:

- критерий Рейнольдса, характеризующий отношение сил инерции к силам вязкости и определяющий характер движения жидкости

где w - скорость потока, м/с;

l - характерный размер, м;

 - коэффициент кинематической вязкости, м²/с;

- критерий Фруда, определяющий отношение сил инерции к силам тяжести

,

где g - ускорение силы тяжести, м/сек²;

- критерий Эйлера, характеризующий соотношений между силами давления и силами инерции

,

где р и р - давление и перепад давления в потоке жидкости, Н/м² (Па);

 - плотность жидкости, кг/м³.

Из дифференциального уравнения энергии получен:

- критерий Пекле, характеризующий отношение удельного потока тепла переносимого конвекцией, движущейся жидкости к удельному потоку тепла переносимому теплопроводностью

где , коэффициент температуропроводности, м²/с.

При решении задач нестационарного теплообмена используются также следующие критерии:

критерий Фурье, имеющий смысл обобщенного времени и характеризующий связь между скоростью изменения температурного поля и физическими свойствами и размерами тела.

,

где , параметр времени, сек;

критерий Био, характеризующий отношение термического сопротивления твердой стенки с толщиной l и коэффициентом теплопроводности  к термическому сопротивлению теплоотдачи на границе твердой стенки и жидкости

.

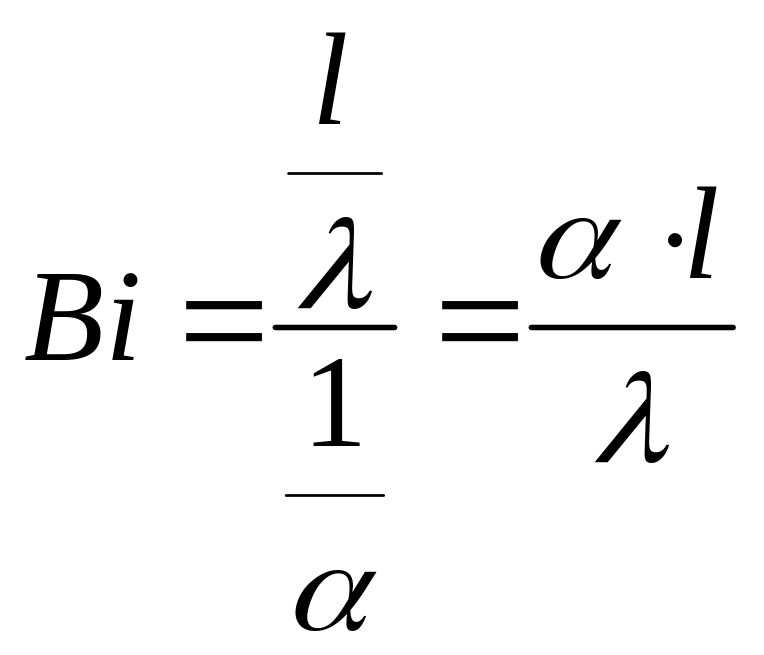Критерий Био аналогичен критерию Нуссельта, но относится к объему твердого тела (=_ст) и является определяющим критерием, т.к.  должно быть равно по условиям однозначности или граничным условиям 3-го рода.

Остальные критерии подобия конвективного теплообмена получают комбинируя полученные ранее критерии:

- критерий Прандтля, характеризующий теплофизические свойства жидкости и определяющий соотношение толщин гидродинамического и теплового пограничного слоя

, откуда ;

- критерий Галилея, характеризующий соотношение силы тяжести и силы вязкого трения

, откуда ;

- критерий Архимеда, определяющий условия свободного движения жидкости в поле силы тяжести

, откуда ,

где , ' и , плотность жидкости в двух точках объема жидкости и изменение плотности жидкости, кг/м³.

Если изменение плотности жидкости получается за счет изменения ее температуры в различных точках (конвективный теплообмен), то в соответствии с газовыми законами

и

где  - коэффициент объемного расширения жидкости, 1/К. Для газов при р=пост =1/Т.

Подставляя в значение критерия Ar получим критерий Грасгофа, характеризующий соотношение подъемной силы, возникающей вследствие разности температуры и плотности жидкости, и силы вязкого трения

.