7.4.6. Пример создания S-функции

case 1,

sys = mdlDerivatives(t,x,M,J,IJ); case 3,

sys = mdlOutputs(x,M,J,IJ); case 9

sys = []; end

% Конец процедуры

%======================================================= function [sys,x0,str,ts] = mdlInitializeSizes(UgSk0,Ug0)

sizes = simsizes; sizes.NumContStates = 3; sizes.NumDiscStates = 0;

sizes.DirFeedthrough = 1; sizes.NumSampleTimes = 1; sys = simsizes(sizes);

x0 = UgSk0; str = [];

ts = [0 0];

% Конец процедуры mdlInitializeSizes %========================================== function z = mdlDerivatives(t,x,M,J,IJ)

%ВХОДНОЙ вектор "M" является вектором проекций моментов внешних сил,

%действующих на космический аппарат соответственно по осям X Y Z

%х(1)=om(1); х(2)=om(2); х(3)=om(3);

%z(1)=d(om(1))/dt; z(2)=d(om(2))/dt; z(3)=d(om(3))/dt;

%|Jxz Jyz Jz |

om=x(1:3); omx=vect2ksm(om);

z=IJ*(M-cross(om,J*om)); % ДИНАМИЧЕСКИЕ уравнения Ейлера

% Конец процедуры mdlDerivatives %================================= function y = mdlOutputs(x,M,J,IJ) y(1:3)=x;

om=x(1:3);

zom=IJ*(M-cross(om,J*om)) ; % Определения УСКОРЕНИЙ y(4:6)=zom;

%Конец процедуры mdlOutputs

Вкачестве входного вектора создаваемого S-блока принят вектор М, со-

стоящий из трех значений текущих проекций момента внешних сил, которые действуют на тело, на оси системы декартових координат, связанной с телом. Образуем выходной вектор y из шести элементов: первые три – текущие значения проекций абсолютной угловой скорости тела, вторые три, - проекции на те же оси абсолютного углового ускорения тела:

y=[omx,omy,omz,epsx,epsy,epsz].

Создаваемый S-блок рассматривается как непрерывная система (с тремя непрерывными состояниями x=[omx,omy,omz]). Поэтому в тексте S-функции изъята процедура mdlUpdate и оставлена процедура mdlDerivative, которая фактически является подпрограммой правых частей динамических уравнений Ейлера.

Создадим новое (пустое) окно блок-схемы SimuLink. Перетянем у него стандартный блок S-функции из раздела Functions & Tables.

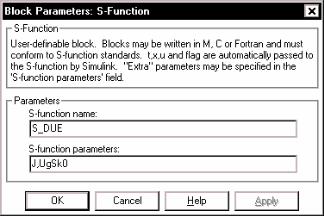
Дважды щелкнув мышью на изображении этого блока, вызовем его окно настраивания и запишем в него название М-файла созданной S-функции и его параметры (рис. 7.101). Нажмем кнопку <OK>.

Рис. 7.101

Вследствие этого на изображении блока возникнет надпись имени S- функции, а окно настраивания исчезнет.

Теперь в том же окне с S-блоком S-функции создадим цепь для проверки правильности его работы.

Но для этого предварительно нужно продумать условия тестового примера. Рассмотрим, например, такой случай:

-на тело не действуют внешние силы, т. е. тело свободно вращается в пространстве;

-оси декартовой системы координат, которая связана жестко с телом, направлены по главным осям инерции тела; при таком условии матрица моментов инерции будет диагональной;

-тело является динамично симметричным, а его ось фигуры направлена вдоль второй оси (Y) связанной системы координат; это означает, что матрица моментов инерции будет иметь вид:

где обозначено: Je - экваториальный момент инерции, J - момент инерции тела относительно его оси фигуры (осевой момент инерции тела), причем J > Je в случае, если тело является сплющенным в направлении оси Y ;

-тело предварительно "раскручено" с угловой скоростью Ω вокруг оси его фигуры и имеет незначительную (по сравнению с Ω) начальную угловую скорость ω0 вокруг оси Х.

Рассмотрим теоретически движение тела при этих условиях. Уравнения Ейлера в этом случае приобретут следующий вид:

−Je ) ωY ωX

иимеют такие решения при заданных начальных условиях:Je Zdt = −(J

причем

Итак, если для образованной модели обеспечить указанные условия, то, если она правильна (адекватна), при моделировании должны получить результаты соответствующие (7.6).

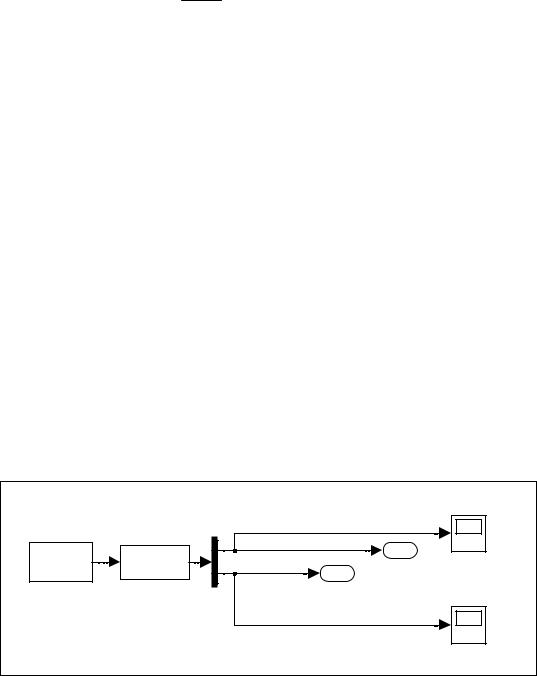
Добавим в блок-схему блок констант, который формирует нулевой вектор моментов внешних сил (рис. 7.102), а также блоки Scope по которым можно проконтролировать результаты моделирования в виде зависимостей от времени проекций угловой скорости и углового ускорения тела.

Перед началом моделирования нужно присвоить значение матрицы моментов инерции. Это можно сделать в командном окне MatLab, вводя строку

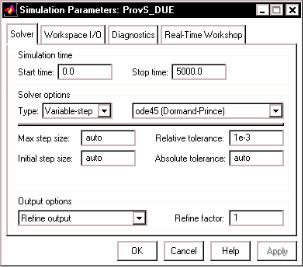
Теперь следует перейти к окну блок-схемы, установить параметры интегрирования, указанные на рис. 7.103 и запустить блок схему на моделирование

Рис. 7.103

По окончании процесса моделирования, обращаясь к окнам блоков Scope, можно убедиться, что созданная модель работает полностью адекватно.

Но убедить в этом читателя довольно трудно из-за следующих обстоятельств. Графические результаты блоков Scope представлены на черном поле. Поэтому скопировать соответствующее графическое окно означает получить некачественное изображение на бумаге, вдобавок израсходовав нерациональное количество красящего материала. Можно скопировать изображение этого окна при помощи команды печати в графическом окне блока Scope, но тогда соответствующее изображение займет целый лист, его невозможно уменьшить средствами текстового редактора. Вдобавок, линии на графике после печати на черно-белом принтере, не будут отличаться один от другого. На них невозможно нанести надписи, чтобы указать особенности кривых, нельзя довольно просто изменить стиль линии.

Все это говорит о том, что наиболее рациональн передать результаты в рабочее пространство с помощью введения выходных портов (рис. 7.102) и подания на них тех сигналов, которые нужно представить графически, а потом построить необходимые графики, пользуясь огромными графическими возможностями

MatLab.

Последнее можно сделать непосредственно, пользуясь командами MatLab в его командном окне, но более рационально сделать это программно, причем желательно объединить в этой программе все действия:

-введение значений параметров, начальных условий и т.п.;

-установление параметров интегрирования;

-обращение к S-модели и запуск ее на моделирование;

-обработку полученных результатов моделирования, построение и оформление графиков.

Пример такой программы приведен ниже.

%Prov_DUEupr.m

%Управляющая программа

%для запуска модели Prov_DUE.mdl

%Лазарев Ю.Ф. 18-12-2001

J=[400 0 0; 0 600 0; 0 0 400]; % Введения значений матрицы инерции

UgSk0=[0.001 0.01 0]; % Введения начальных значений

%проекций угловой скорости тела

%Установления параметров моделирования options=simset('Solver','ode45','RelTol',1e-6); sim('Prov_DUE',5000,options); % МОДЕЛИРОВАНИЯ на S-модели

%Формирования данных и вывод ГРАФИКОВ

tt=tout;

omx=yout(:,1); omy=yout(:,2); omz=yout(:,3); epsx=yout(:,4); epsy=yout(:,5);epsz=yout(:,6);

subplot(2,1,1) h=plot(tt,omx,tt,omy,'.',tt,omz,'--');grid set(h,'LineWidth',2); set(gca,'LineWidth',2) set(gca,'FontAngle','italic','Fontsize',16) title(' Проекции угловых скоростей') ylabel('радианы в секунду') legend('omx','omy','omz',0)

subplot(2,1,2) h=plot(tt,epsx,tt,epsy,'.',tt,epsz,'--');grid set(h,'LineWidth',2); set(gca,'LineWidth',2) set(gca,'FontAngle','italic','Fontsize',16) title('Проекции угловых ускорений ') ylabel('1/c2)')

xlabel('Время (с)') set(gcf,'color','white') legend('epsx','epsy','epsz',0)

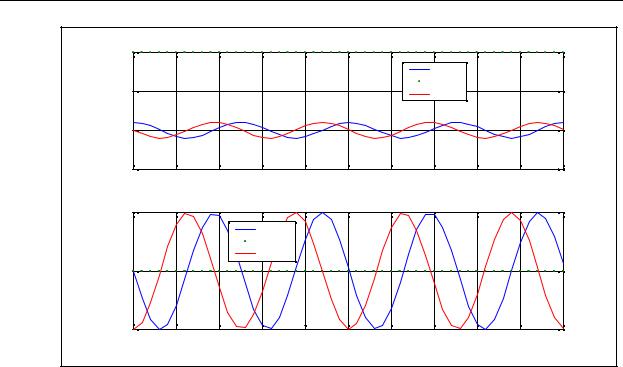
Обратившись к этой программе, получим графики, приведенные на рис.

7.104.

Теперь читатель может наглядно убедиться в правильности модели.

set_param('MODEL','PreLoadFcn','PERVdan')

Если после выполнения этой команды записать на диск эту S-модель, то при дальнейших ее вызовах сначала автоматически будет вызван и выполнен файл PERVdan.m и лишь после этого на экране возникнет блок-схема S-модели, готовая к моделированию.

Проверить, какой именно m-файл используется в данной S-модели как предварительно выполняемый, можно путем привлечения команды

get_param('имя S-модели','PreLoadFcn')

Если же нужно вызвать некоторый m-файл перед или после проведения собственно моделирования на S-модели (например, нужно вызвать программу, которая позволяет изменить установленные значения параметров модели в диалоговом режиме, или использовать программу вывода результатов моделирования в графической форме), можно установить на свободном месте блок-схемы пустые блоки Subsystem (из раздела Sygnals & System), каждый из которых будет осуществлять вызов соответствующего m-файла.

После установления блока Subsystem в поле блок-схемы модели следует щелкнуть правой клавишою мышки на его изображении. В окне, которое возник-

нет, следует выбрать команду Block propertіes. Возникнет окно настраивания блока, изображенное на рис. 7.105.

Рис. 7.105

Теперь достаточно внести имя m-файла (например, как на рис. 7.105, - ModelMENU) в окошко Open function окна настраивания блока, возвратиться в окно блок-схемы и сделать надпись на установленном блоке Subsystem, которая раскрывала бы его назначение.

Если m-файл, имя которого вписано в окно настраивания блока Subsystem,

существует, то его выполнение теперь можно осуществить, дважды щелкнув мышью на изображении этого блока.

Осуществление связи S-модели с определенными m-файлами описанным способом, наверное, является, пожалуй, наиболее удобным, так как, во-первых, позволяет вызвать m-файлы лишь в случае необходимости и в произвольном порядке, а во-вторых, все управление моделированием и вызовом программ осуществляется только из блок-схемы S-модели.