
- •Начала программирования в среде MatLab
- •Содержание
- •Предисловие
- •Введение
- •1. MatLAB как научный калькулятор
- •1.1. Командное окно
- •1.2. Операции с числами
- •1.2.1. Ввод действительных чисел
- •1.2.2. Простейшие арифметические действия
- •1.2.3. Ввод комплексных чисел
- •1.2.4. Элементарные математические функции
- •1.2.5. Специальные математические функции
- •1.2.6. Элементарные действия с комплексными числами
- •1.2.7. Функции комплексного аргумента
- •1.2.8. Задания
- •1.2.9. Вопросы
- •1.3. Простейшие операции с векторами и матрицами
- •1.3.1. Ввод векторов и матриц
- •1.3.2. Формирование векторов и матриц
- •1.3.3. Извлечение и вставка частей матриц
- •1.3.4. Действия над векторами
- •1.3.5. Поэлементное преобразование матриц
- •1.3.6. Матричные действия над матрицами
- •1.3.7. Матричные функции
- •1.3.8. Задания
- •1.3.9. Вопросы
- •1.4. Функции прикладной численной математики
- •1.4.1. Операции с полиномами
- •1.4.2. Обработка данных измерений
- •1.4.3. Функции линейной алгебры
- •1.4.4. Аппроксимация и интерполяция данных
- •1.4.5. Векторная фильтрация и спектральный анализ
- •1.4.6. Задания
- •1.4.7. Вопросы
- •1.5. Построение простейших графиков
- •1.5.1. Процедура plot
- •1.5.2. Специальные графики
- •1.5.3. Дополнительные функции графического окна
- •1.5.5. Задания
- •1.5.6. Вопросы
- •1.6. Операторы управления вычислительным процессом
- •1.6.1. Оператор условного перехода
- •1.6.2. Оператор переключения
- •1.6.3. Операторы цикла
- •1.6.4. Задания
- •1.6.5. Вопросы
- •2. Программирование в среде MatLAB
- •2.1. Функции функций
- •2.2. Создание М-файлов
- •2.2.1. Особенности создания М-файлов
- •2.3.1. Общие требования к построению
- •2.3.2. Типовое оформление процедуры-функции
- •2.3.3. Задания
- •2.3.4. Вопросы
- •2.4. Создание Script-файлов
- •2.4.1. Основные особенности Script-файлов
- •2.4.2. Ввод и вывод информации в диалоговом режиме
- •2.4.3. Организация повторения действий
- •2.4.4. Организация изменения данных в диалоговом режиме
- •2.4.5. Типовая структура и оформление Script-файла
- •2.5. Графическое оформление результатов
- •2.5.1. Общие требования к представлению графической информации
- •2.5.2. Разбивка графического окна на подокна
- •2.5.3. Вывод текста в графическое окно (подокно)
- •2.6. Создание функций от функций
- •2.6.1. Процедура feval
- •2.6.2. Примеры создания процедур от функций
- •2.6.3. Задания
- •2.7. Пример создания сложной программы
- •2.7.1. Программа моделирования движения маятника
- •2.7.2. Задания
- •3.1. Функции меню командного окна
- •3.1.2. Другие меню командного окна
- •3.1.3. Панель инструментов
- •3.2. Команды общего назначения
- •3.3. Создание М-книги
- •3.3.1. Начало новой М-книги
- •3.3.2. Написание М-книги
- •3.3.3. Редактирование М-книги
- •3.3.4. Преобразование документа WORD в М-книгу
- •3.3.6. Изменение параметров вывода результатов
- •4. Классы вычислительных объектов
- •4.1. Основные классы объектов
- •4.1.1. Класс символьных строк (char)
- •4.1.2. Класс записей (struct)
- •4.1.3. Класс ячеек (cell)
- •4.2. Производные классы MatLAB
- •4.2.1. Класс объектов Inline
- •4.2.2. Классы пакета CONTROL
- •4.3. Пример создания нового класса polynom
- •4.3.1. Создание подкаталога @polynom
- •4.3.2. Создание конструктора
- •4.3.3. Создание процедуры символьного представления polynom-объекта.
- •4.4. Создание методов нового класса
- •5.1. Формирование типовых процессов
- •5.1.1. Формирование одиночных импульных процессов
- •5.1.2. Формирование колебаний
- •5.2.1. Основы линейной фильтрации
- •5.2.2. Формирование случайных процессов
- •5.3. Процедуры спектрального (частотного) и статистического анализа процессов
- •5.3.1. Основы спектрального и статистического анализа
- •5.3.2. Примеры спектрального анализа
- •5.3.3. Статистический анализ
- •5.4. Проектирование фильтров
- •5.4.1. Формы представления фильтров и их преобразования
- •5.4.2. Разработка аналоговых фильтров
- •5.4.3. Проектирование БИХ-фильтров
- •5.5. Графические и интерактивные средства
- •5.5.1. Графические средства пакета SIGNAL
- •5.5.2. Интерактивная оболочка SPTOOL
- •6.1. Ввод и преобразование моделей
- •6.2. Получение информации о модели
- •6.3. Анализ системы
- •6.4. Интерактивный "обозреватель" ltiview
- •6.5. Синтез системы
- •7.1. Общая характеристика пакета SimuLink
- •7.1.1. Запуск SimuLink
- •7.1.2. Библиотека модулей (блоков)
- •7.1.3. Раздел Sinks (приемники)
- •7.1.4. Раздел Sources (Источники)
- •7.1.5. Раздел Сontinuous
- •7.1.6. Раздел Discrete
- •7.1.7. Раздел Math
- •7.1.8. Раздел Functions & Tables
- •7.1.9. Раздел Nonlinear
- •7.1.10. Раздел Signals & Systems
- •7.2. Построение блок-схем
- •7.2.1. Выделение объектов
- •7.2.2. Оперирование с блоками
- •7.2.3. Проведение соединительных линий
- •7.2.4. Проставление меток сигналов и комментариев
- •7.2.5. Создание подсистем
- •7.2.6. Запись и распечатка блок-схемы S-модели
- •7.3. Примеры моделирования
- •7.3.1. Моделирование поведения физического маятника
- •7.3.2. Моделирование поведения гироскопа в кардановом подвесе
- •7.4. Объединение S-моделей с программами MatLAB
- •7.4.2. Функции пересечения нуля
- •7.4.5. Образование S-блоков путем использования программ MatLab. S-функции
- •7.4.6. Пример создания S-функции
- •7.5.1. Создание библиотеки
- •7.5.2. Маскировка блоков
- •7.5.3. Моделирование процесса ориентации космического аппарата
- •Послесловие
- •Предметный указатель
- •Указатель операторов, команд, функций и функциональных блоков MatLAB
7.3. Примеры моделирования |
368 |
|
|
|
|
линий; в особенности неудобно то, что здесь не предусмотрены средства вывода текстовой информации на поле графика, что делает графическое представление безадресным.
Последний недостаток существенен. Он может быть устранен существующими в пакете SIMULINK средствами. Например, можно записать полученные значения исходных величин в MAT-файл (посылая их на блок To File), а потом создать и использовать программу, которая бы осуществляла считывание данных, записанных в МАТ-файле, и формирование на этой основе графического изображения в окне фигуры по образцу, приведенному в разделах 2.5 и 2.7. Такой путь использован в следующем примере. Неудобством применения обзорного окна XY Graph является также то, что предварительно нужно установить диапазоны изменения обеих входных величин по осям графика. Если эти диапазоны установлены неверно, в обзорном окне может вообще не возникнуть изображение графика, или появится такой его фрагмент, по которому невозможно сделать правильный вывод о поведении исследуемой системы. А при исследовании системы часто невозможно заранее предусмотреть диапазоны изменений величин, или сделать это слишком сложно.
7.3.2. Моделирование поведения гироскопа в кардановом подвесе
Уравнения движения гироскопа в кардановом подвесе на неподвижном основании представим в виде (см. Задача 2.19, раздел 2.6)
|
+ J2 cos |
2 |
&& |
|
& & |
|
|
& |
|
|
||
(J1 |
|
β)α −2J |
2αβsin |
βcos β + Hβ cos β = |
|
|||||||
|
& |
0 + Nm sin(ωt +εN ) −[R0 + Rm sin(ωt +εR )]sin β, |
||||||||||
= − f2α + N |
||||||||||||
|
&& |
|
|
|
|
|
|
|
|
& |
+ L0 |
+ |
J3 β + J2αsin βcos β − Hα cos β = − f2 β |
||||||||||||
|
|
|
& |
|
|
|
& |
|
|
|
|
|
+ Lm sin(ωt +εL ), |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
dH |
= R |
+ R |
sin(ωt +ε |
|
), |
|
|
|
|
|
|
|
|
R |
|
|
|||||
|
|
|
dt |
0 |
m |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Воплощение этой системы уравнений в блок-схему S-модели показано на |
||||||||||||
рис. 7.79...7.82. |
|
|
|
|
|
|
|
|
|
|
|
|
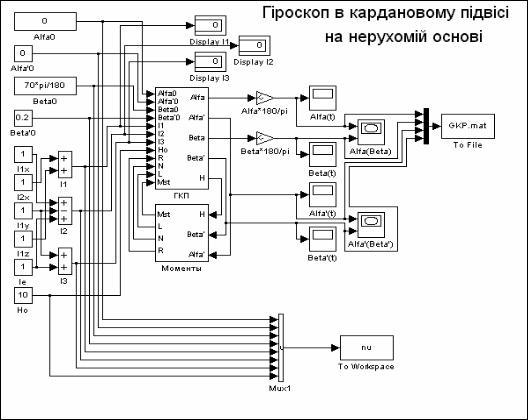
Рисунок 7.79 |
представляет основную модель. |
|
|
|||||||||
Основная S-модель содержит в себе такие основные компоненты:
блоки задания исходных данных; это совокупность блоков типа Constant, определяет значения постоянных величин, входящих в уравнения гироскопа:
две основных подсистемы (построенные на основе стандартных блоков
Subsystem): ГКП и Моменты;
ряд блоков построения графических изображений исходных процессов; среди них 4 блока типа Scope и два блока типа XYGraph; назначение каждого из них становится понятным из рассмотрения блок-схемы;
7.3. Примеры моделирования |
369 |
|
|
|
|
блок типа To File, записывающий полученные вычисленные значения углов α и β , а также угловых скоростей гироскопа α& и β& и модельного времени t в файл GKP. mat.
Рис. 7.79
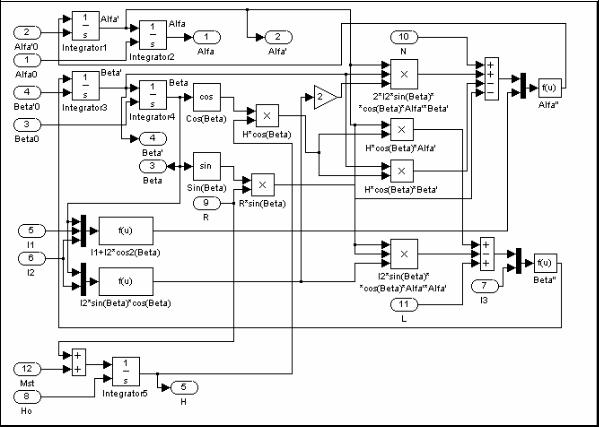
Схема подсистемы ГКП представлена на следующем рисунке (7.80). Подсистема осуществляет численное интегрирование исходной системы
дифференциальных уравнений. Здесь размещены 5 интеграторов (так как принятая система дифференциальных уравнений имеет пятый порядок). Входы с 1 по 8, 12 и 13 представляют величины, которые не изменяются в процессе моделирования. Входы же из 9 по 11 являются моментами сил, действующие по осям подвеса гироскопа, значения которых формируются в подсистеме Моменты. Число выходов в этой подсистеме - 5. Сюда входят два угла поворота гироскопа, две их производные по времени и текущее значение собственного кинетического момента гироскопа.
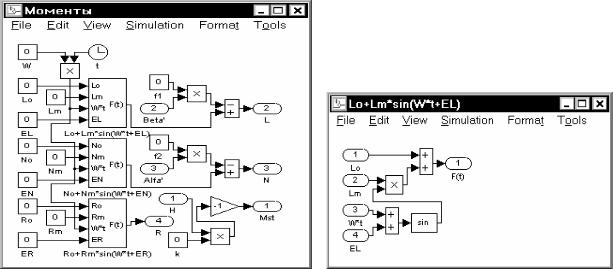
Подсистема Моменты (рис. 7.81) использует данные об угловых скоростях поворота гироскопа и текущее значение кинетического момента для формирования величин моментов сил сопротивления (трения) по осям подвеса. Блок Моменты имеет 3 входа. Кроме этого, внутри подсистемы осуществляется установка 13 постоянных параметров, которые определяют коэффициенты трения по осям и параметры гармонических колебаний моментов. Выходами подсистемы являются текущие значения моментов сил по каждой из трех осей карданового подвеса. Формирование составляющих моментов сил, изменяющихся
7.3. Примеры моделирования |
370 |
|
|
|
|
гармонически, происходит по однотипному правилу, воплощенному в трех полностью аналогичных под-подсистемах, одна из которых представлена на рис. 7.82.
Рис. 7.80
Как вытекает из схемы черт. 7.79, на вход конечного файла GKP. mat подаются 4 величины: первая сверху - α , вторая - β , третья - угловая скорость
гироскопа α& и четвертая - β&. Это значит, что в файл с указанным именем будет
записываться матрица, состоящая из 5 строк. В первую строку будет записан массив значений модельного времени, для которых вычислены значения выходных (относительно S-модели) величин. В остальные строки будут записаны значения величин, являющихся входами блока То File, причем сверху вниз в порядке расположения самих входов этого блока.
|
7.3. Примеры моделирования |
371 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.81 |
Рис. 7.82 |
Если файл GKP. mat сформирован (а это произойдет автоматически при запуске основной S-модели путем нажатия команды Start меню Simulation), появляется возможность использовать записанные данные в специальном Scriptфайле для оформления графического окна с необходимым текстовым оформлением.
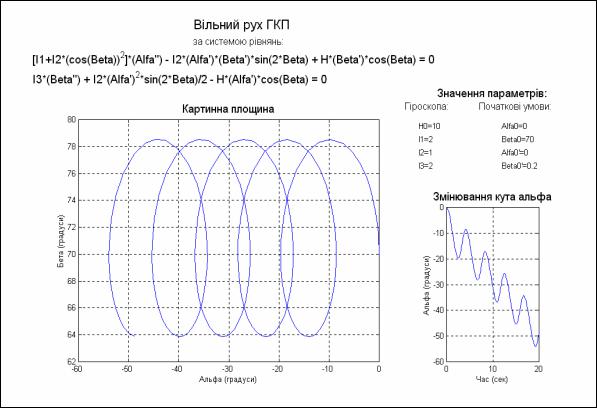
Далее приведен текст варианта такого Script-файла. Запуская этот Scriptфайл после проведения вычислений, получим графическое окно, представленное на рис. 7.83.
Script-файл GKP_graf
%Считывание исходных данных из записанной в переменной "nu" рабочего пространства
%информации (см. блок To Workspace схемы рис. 7.33)
Alfa0=nu(1,1)*180/pi; Beta0=nu(1,3)*180/pi; Alfat0=nu(1,2); Betat0=nu(1,4); I1=nu(1,5); I2=nu(1,6); I3=nu(1,7); H0=nu(1,8);
load GKP; % Загрузка (чтения) файла GKP. mat
%( Происходит присваивание системной переменной ANS значений
%всей матрицы, которая содержится в файле GKP. mat.
%При этом модельное время занимает первую строку этой матрицы,
%а массивы входных величин - следующие строки матрицы
%в порядке указания входов в блок To File сверху вниз )
%Теперь выделяем отдельные строки матрицы ANS и присваиваем им
%имена соответствующих переменных исходных уравнений
tout=ans(1,:); |
Alfa=ans(2,:); |
Beta=ans(3,:); |
Alfat=ans(4,:); |
Betat=ans(5,:); |
|
set(gcf,'Color','white') |
|
|
%Оформление графического подокна "alfa(t)"
subplot(4,4,[12 16]); plot(tout,Alfa);grid;
title('Изменение угла альфа','FontSize',12); xlabel('Время (сек)','FontSize',8); ylabel('Альфа (градусы)','FontSize',8);
% Оформление графического подокна "Картинная плоскость"
subplot(4,6,[7 22]);
7.3. Примеры моделирования |
372 |
|
|
|
|
plot(Alfa,Beta);grid;
title('Картинная плоскость','FontSize',14); xlabel('Альфа (градусы)','FontSize',10); ylabel('Бета (градусы)','FontSize',10);
Рис. 7.83
%Оформление текстового подокна "Модель"
subplot(4,4,1:4);
axis('off');
h1=text(0.25,1.1,'Свободное движение ГКП','FontSize',16); h1=text(0.25,0.85,'по системе уравнений:','Fontsize',12); h1=text(-0.1,0.6,'[I1+I2*(cos(Beta))2]*(Alfa'''') - I2*(Alfa'')*(Beta'')*sin(2*Beta) +
H*(Beta'')*cos(Beta) = 0','Fontsize',14);
h1=text(-0.1,0.3,'I3*(Beta'''') + I2*(Alfa'')2*sin(2*Beta)/2 - H*(Alfa'')*cos(Beta) = 0','Fontsize',14);
%Оформление текстового подокна "Параметры"
subplot(4,4,8);
axis('off');
h1=text(-0.1,1.4,'Значения параметров:','Fontsize',14); h1=text(-0.45,1.2,'Гироскопа:','Fontsize',12); h1=text(0.35,1.2,'Начальные условия:','Fontsize',12); h1=text(-0.3,0.9,sprintf('H0=%g',H0),'Fontsize',10); h1=text(-0.3,0.7,sprintf('I1=%g',I1),'Fontsize',10);
