1.4. Функции прикладной численной математики |
|
|
66 |
||
|
1 |
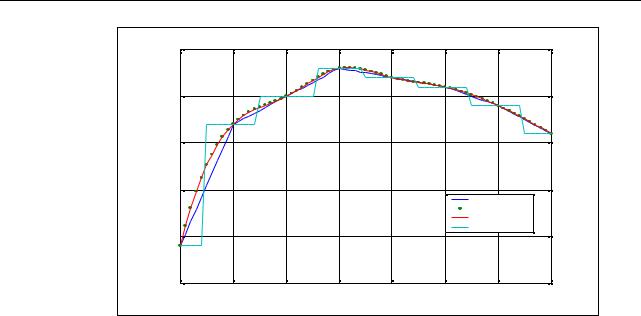
Интерполяция процедурой INTERP1 |
|
||
|
|
|
|
|
|
|
0.5 |
|
|
|
|
Функция |
0 |
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
линейная |
|
|
|
|
|
|
|
|
|
|
|
|
кубическая |
|
|
|
|
|
сплайновая |
|
|
-1 |
|
|
ступенчатая |
|
|
|
|
|
|
|
|
-1.5 |
-0.4 -0.3 -0.2 -0.1 |
0 |
0.1 |
0.2 |
|
-0.5 |
||||
|
|
Аргумент |
|
|
|
|
|
Рис. 1.20 |
|
|
|
1.4.5.Векторная фильтрация и спектральный анализ
Всистеме MatLAB есть несколько функций для проведения цифрового анализа данных наблюдений (измерений).
Так, функция y = filter(b,a,x) обеспечивает формирование вектора y по заданным векторам b, a, x в соответствии с соотношением:
y(k) = b(1)*x(k) + b(2)*x(k-1) + ... + b(nb+1)*x(k-nb) -
-a(2)*y(k-1) - a(3)*y(k-3) - ... - a(na+1)*y(k-na), |
(1.1) |
где вектор b имеет такой состав
b = [ b(1), b(2),... , b(nb+1)],
a вектор а
a = [1, a(2), a(3),... , a(na+1)].
Соотношение (1) можно рассматривать как конечно-разностное уравнение фильтра с дискретной передаточной функцией вида рациональной дроби, коэффициенты числителя которого образовывают вектор b, а знаменателя - вектор а, на вход которого подается сигнал x(t), а на выходе формируется сигнал y(t).
Тогда вектор y будет представлять собой значение исходного сигнала этого фильтра в дискретные моменты времени, соответствующие заданным значениям входного сигнала x(t) (вектор х).
Ниже приведен пример применения функции filter.
»x = 0:0.1:1;
»b = [1 2];
»a = [ 1 0.1 4];
»y = filter(b,a,x)
y =
Columns 1 through 7
0 0.1000 0.3900 0.2610 -0.5861 0.3146 3.9129 Columns 8 through 11
0.2503 -13.4768 2.8466 56.4225
1.4. Функции прикладной численной математики |
67 |
Функции fft (Fast Fourier Transformation) и ifft (Invers Fast Fourier Transformation) осуществляют преобразование заданного вектора, сооствествующие дискретному прямому и обратному преобразованиям Фурье.
Обращение к этим функциям вида: y = fft ( x, n ); x = ifft ( y, n )
приводит к формированию вектора y в первом случае и х - в втором по формулам:
y(k) = |
|
n |
(m−1) (k −1) / n ; |
|
|
|
∑x(m) e− j 2π |
(1.2) |
|||
|
m=1 |
|
|
||
|
|
1 n |
|
|
|
x(m) = |
|
|
∑ y(k) e j 2π (m−1) (k −1) / n , |
(1.3) |
|
|
|
||||
|
|
n k =1 |
|
|
|
где j - обозначение мнимой единицы; n - число элементов заданного вектора х (оно представляет также размер выходного вектора y).
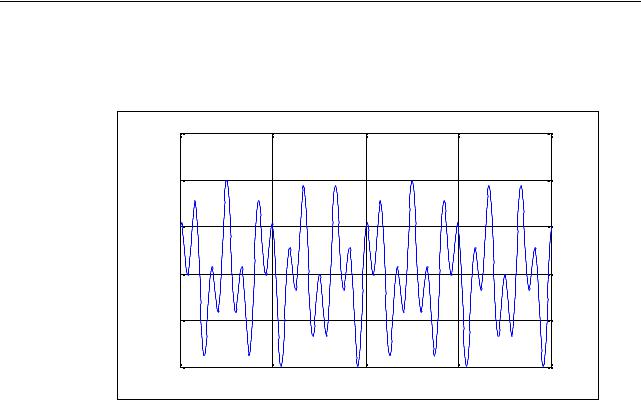
Приведем пример. Сформируем входной сигнал в виде вектора, элементы которого равняются значениям функции, являющейся суммой двух синусоид с частотами 5 и 12 Гц (рис. 1.21).
t =0:0.001:2;
x = sin(2*pi*5*t) + cos(2*pi*12*t); plot(t, x); grid set(gcf,'color','white')
set(gca,'FontName','Arial Cyr','FontSize',16), title('Входной процесс ');
xlabel('Время (с)'); ylabel('Х(t)')
|
2 |
|
Входной процесс |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Х(t) |
0 |
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
-20 |
0.5 |
1 |
1.5 |
2 |
|
|
|
Время (с) |
|
|
|
|
|
Рис. 1.21 |
|
|
Найдем Фурье-изображение этого сигнала и выведем графическое представление модуля його Фурье-изображения:
y = fft(x);
1.4. Функции прикладной численной математики |
68 |
a =abs(y); plot(a); grid
set(gca,'FontName','Arial Cyr','FontSize',16), title('Модуль Фурьє - изображения '); xlabel('Номер элемента вектора'); ylabel('abs(F(X(t))')
Результат отображен на рис. 1.22.
abs(F(X(t))
Модуль Фурьє - изображения
1200
1000
800
600
400
200
00 |
500 |
1000 |
1500 |
2000 |
2500 |
|
Номер элемента вектора |
|
|||
|
|
Рис. 1.22 |
|
|
|
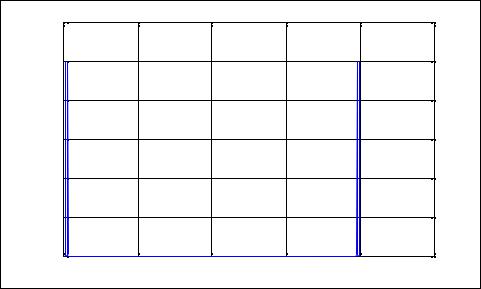
Теперь осуществим обратное преобразование с помощью функции ifft и результат также выведем в форме графика:
z = ifft(y); plot(t, z); grid
set(gca,'FontName','Arial Cyr','FontSize',16), title('Обратное Фурье-преобразование '); xlabel('Время (с)');
ylabel('Z(t)')
На рис. 1.23 изображен результат. Рассматривая его, можно убедиться, что воспроизведенный процесс точно совпадает с исходным.
Внимательно изучая формулу дискретного преобразования Фурье, можно заметить:
а) номер m отвечает моменту времени tm, в который измерен входной сигнал x(m); при этом t1 = 0;
б) номер k - это индекс значения частоты fk, которому отвечает найденный элемент y(k) дискретного преобразования Фурье;
в) чтобы перейти от индексов к временной и частотной областям, необходимо знать значение h дискрета (шага) времени, через который измерен входной сигнал x(t) и промежуток T времени, на протяжении которого он измеряется; тогда шаг (дискрет) по частоте в изображении Фурье определится соотношением:
Df = 1/T, (1.4)
а диапазон изменения частоты - формулой
1.4. Функции прикладной численной математики |
|
69 |
||
|
F = 1/h; |
|
(1.5) |
|
так, в анализируемом примере (h =0. 001, T = 2, n = 21): |
|
|||
|
Df = 0.5; |
F = 1000; |
|
|
3 |
Обратное Фурье-преобразование |
|
||
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
Z(t) |
|
|
|
|
0 |
|
|
|
|
-1 |
|
|
|
|
-20 |
0.5 |
1 |
1.5 |
2 |
|
|
Время (с) |
|
|
|
|
Рис. 1.23 |
|
|
г) из (2) следует, что индексу k = 1 отвечает нулевое значение частоты (f0 = 0); иначе говоря, первый элемент вектора y(1) является значением Фурьеизображения при нулевой частоте, т. е. - просто суммой всех заданных значений вектора x; отсюда получаем, что вектор y(k) содержит значение Фурьеизображения, начиная из частоты f0 = 0 (которой отвечает k = 1) до максимальной частоты fmax = F (которой отвечает k = n); таким образом, Фурье-изображение определяется функцией fft только для положительных частот в диапазоне от 0 к F; это неудобно для построения графиков Фурье-изображения от частоты; более удобным и привычным представляется переход к вектору Фурье-изображения, определенному в диапазоне частот от (-F/2) до F/2; частота FN = F / 2 получила
название частоты Найквиста;
д) как известно, функция e j z является периодической по z с периодом 2π ; поэтому информация об Фурье-изображении при отрицательных частотах расположена во второй половине вектора y(k).
Сформируем для анализируемого примера массив частот, исходя из вышеупомянутого:
f = 0 : 0.5 : 1000;
и выведем графік с аргументом-частотой (рис. 1.24): plot(f,a); grid
set(gca,'FontName','Arial Cyr','FontSize',16), title('Модуль Фурье - изображения '); xlabel('Частота (Гц)');
ylabel('abs(F(X(t))')
1.4. Функции прикладной численной математики |
70 |
Как следует из рассмотрения рис. 1.24, по нему непросто распознать те частоты (5 и 12 Гц), с которыми изменяется входной сигнал. Это - следствие того обстоятельства, которое было отмечено в примечании г). Чтобы определить частотный спектр входного сигнала, нужно сначала преобразовать полученный вектор y Фурье-изображения с помощью процедуры fftshift.
abs(F(X(t))
Модуль Фурье - изображения
1200
1000
800
600
400
200
00 |
200 |
400 |
600 |
800 |
1000 |
|
|
Частота (Гц) |
|
|
|
|
|
Рис. 1.24 |
|
|
|
Функция fftshift (обращение к ней осуществляется таким образом: z = fftshift(y)) предназначена для формирования нового вектора z из заданного вектора y путем перестановки второй половины вектора y в первую половину вектора z . При этом вторая половина вектора z состоит из элементов первой половины вектора y. Более точно эту операцию можно задать соотношениями:
z(1) = y(n/2+1); ... , z(k) = y(n/2+k);... , z(n/2) = y(n); z(n/2+1) = y(1);...
..., z(n/2+k) = y(k);... z(n) = y(n/2).
Примечание. Операцию fftshift удобно использовать для преобразования массива Фурье-изображение с целью построения его графика в частотной области. Тем не менее этот массив не может быть использован для обратного преобразования Фурье.
Проиллюстрируем применение этой функции к предыдущему примеру: f1 = -500 : 0.5 : 500; % Перестройка вектора частот
v = fftshift(y); % Перестройка вектора Фурье-изображения a =abs(v); % Отыскание модуля
% Вывод графика plot(f1(970:1030),a(970:1030)); grid set(gca,'FontName','Arial Cyr','FontSize',16), title('Модуль Фурье - изображения'); xlabel('Частота (Гц)'); ylabel('abs(F(X(t))')