4.4. Создание методов нового класса

Проверим корни созданного полинома, используя процедуру roots (см. да-

лее):

>> roots(Pol2) ans = 5.0000

4.0000

3. 0000

2.0000

1.0000

Как свидетельствует результат, все созданные М-файлы работают нормально.

4.4. Создание методов нового класса

Весьма удобной в системе MatLAB является предоставляемая ею возможность создания процедур, которые могут быть выполнены не только стандартным путем обращения к ее имени, но и более простым путем использования знаков арифметических действий, операций сравнения, скобок и т.п. С этим мы уже столкнулись в предыдущем разделе, убедившись, что процедура display выполняется не только при явном обращении вида display(х), но и неявно, если некоторый оператор формирует величину х, а после этого оператора отсутствует символ ' ; '.

Поэтому, если в любом новом классе объектов присутствует М-файл с именем display, он будет выполняться во всех случаях, когда очередной оператор, создающий объект этого класса, не заканчивается точкой с запятой.

Приведем перечень имен таких М-файлов, предусмотренных системой MatLAB, с указанием вида оператора их неявного вызова и краткого описания особенностей их использования.

Перечисленные процедуры в MatLAB могут быть переопределены под теми же именами во всех новообразованных подкаталогах новых классов. После этого обычные операторы арифметических действий и операций сравнения могут применяться и при оперировании объектами новых классов. Смысл этих операций, конечно, может значительно отличаться от обычного и будет определяться содержимым соответствующих М-файлов в подкаталогах классов.

Учитывая это, можно сделать вывод, что М-файлов с названиями, указанными в таблице 3.1, может быть много. MatLAB различает их по типу аргументов, указанных в перечне входных параметров.

Создадим, например, операцию (метод) сложения полиномов, используя операторную процедуру plus. Текст соответствующего М-файла для подкаталога @POLYNOM приведен ниже.

function r=plus(p,q)

% POLYNOM/PLUS Сложение полиномов r = p + q p = polynom(p);

q = polynom(q); k = q.n - p.n;

r= polynom([zeros(1,k) p. c]+[zeros(1,-k) q. c]);

%Завершение POLYNOM/PLUS

Сначала процедура превращает оба аргумента в класс polynom. Это нужно для того, чтобы метод работал и тогда, когда один из аргументов задан как вектор, или когда в качестве аргумента используется выражение типа p + r, где p - поли- ном-объект, а r - число. Затем процедура дополняет нулями векторы коэффициентов полиномов-слагаемых, если в этом возникает необходимость (при неодинаковых порядках полиномов). Фактически сложение сводится к сложению этих исправленных векторов коэффициентов. Заключительная операция - по полученному вектору полинома суммы создается новый полином-объект с помощью конструктора полиномов. Проиллюстрируем работу этого метода на примере. Введем вектор коэффициентов первого полинома:

>>V1 = [ 2-3 0 6];

исоздадим из него полином-объект

>>P1 = polynom(V1)

P1 = 2*x3-3*x2 + 6;

Аналогично создадим второй полином:

>>V2=[2 0 0 9 0 0 -3 +5];

>>P2=polynom(V2)

P2 = 2*x^7 + 9*x^4 - 3*x + 5;

Сложим эти полиномы:

>> P1+P2

В результате получим:

ans = 2*x7 + 9*x4 + 2*x3-3*x2-3*x + 11;

Аналогичные результаты получаются и в случае, если один из аргументов "ошибочно" представлен вектором:

>> P1+V2

ans = 2*x^7 + 9*x^4 + 2*x^3 - 3*x^2 - 3*x + 11;

>> V1+P2

ans = 2*x7 + 9*x4 + 2*x3-3*x2-3*x + 11;

Однако если оба аргумента представлены векторами, система сразу же отреагирует на это, обнаружив ошибку:

>> V1+V2

??? Error using Î +

Matrix dimensions must agree.

В этом случае система уже использует не М-файл plus из подкаталога @POLYNOM, а встроенную аналогичную процедуру для векторов. А эта процедура осуществляет сложение векторов лишь при условии их одинаковой длины. Поэтому и возникает ошибка.

Аналогичной является процедура вычитания полином-объектов:

function r=minus(p,q)

% POLYNOM/MINUS Вычитание полиномов r = p - q p = polynom(p);

q = polynom(q); k = q.n - p.n;

r= polynom([zeros(1,k) p. c]-[zeros(1,-k) q. c]);

%Завершение POLYNOM/MINUS

Проверим ее работу на примере:

>> P1-P2

ans = -2*x7-9*x4 + 2*x3-3*x2 + 3*x + 1;

Создадим еще такие методы класса polynom:

-метод double, который осуществляет обратную относительно создания по- лином-объекта операцию, - по заданному полиному определяет вектор его

коэффициентов и порядок: function [v,n]=double(p)

%POLYNOM/DOUBLE - преобразование полином-объекта

%в вектор его коэффициентов

%v=DOUBLE(p) превратит полином-объект "р" в вектор "v",

%содержащий коэффициенты полинома в порядке уменьшения

%степени аргумента

%Обращение [v,n]=DOUBLE(p) позволяет получить также

%значение "n" порядка этого полинома.

v= p.c;

n= p. n; % Завершение POLYNON/DOUBLE

- метод diff, который создает полином-объект, являющийся производной от заданного полинома

function q = diff(p)

%POLYNOM/DIFF формирует полином-производную "q"

%от заданного полинома "р"

p = polynom(p); d = p.n;

q= polynom(p. c(1:d). *(d:-1:1)); % Завершение POLYNOM/DIFF

-метод mtimes; он создает полином-объект, являющийся произведением двух заданных полиномов:

function r = mtimes(p,q)

% POLYNOM/MTIMES Произведение полиномов: r = p * q p = polynom(p);

q = polynom(q);

r = polynom(conv(p. c,q. c)); % Завершение POLYNOM/MTIMES

-метод mrdivide; он создает два полином-объекта, один из которых является частным от деления первого из указанных полиномов на второй, а второй –

остатком такого деления:

function rez = mrdivide(p,q)

% POLYNOM/MRDIVIDE Деление полиномов: r = p / q p = polynom(p);

q = polynom(q); [rr,ro]=deconv(p.c,q.c); rez{1}=polynom(rr);

rez{2}=polynom(ro); % Завершение POLYNOM/MRDIVIDE

- метод roots создает вектор корней заданного полинома: function r = roots(p)

% POLYNOM/ROOTS вычисляет вектор корней полинома "р" p = polynom(p);

r = roots(p. c); % Завершение POLYNOM/ROOTS

- метод polyval вычисляет вектор значений заданного полинома по заданному вектору значений его аргумента:

function y = polyval(p,x)

%POLYNOM/POLYVAL вычисляет значение полинома "р"

%по заданному значению аргумента "х"

p = polynom(p); y =0;

for a = p.c

y = y. *x + a;

end % Завершение POLYNOM/POLYVAL

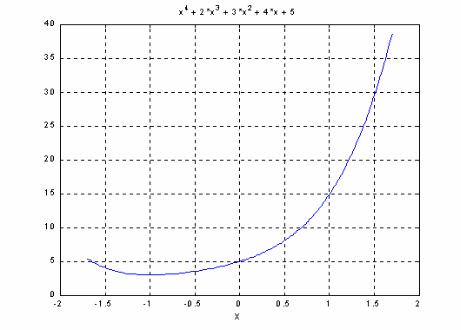
- метод plot строит график зависимости значений заданного полинома в диапазоне значений его аргумента, который содержит все его корни:

function plot(p)

% POLYNOM/PLOT построение графика полинома "р" p=polynom(p);

r= max(abs(roots(p.c))); x=(-1.1:0.01:1.1)*r;

y= polyval(p.c,x); plot(x,y); grid; title(char(p));

xlabel('X'); % Завершение POLYNOM/PLOT

- метод rdivide(p,xr) осуществляет деление полинома p на число xr: function r = rdivide(p,xr)

% POLYNOM/RDIVIDE Правое деление полинома на число: r = p / xr p = polynom(p);

r. c = p. c/xr;

r = polynom(r. c); % Завершение POLYNOM/RDIVIDE

Проверим действие некоторых из созданных методов:

>> Pol = polynom([1 2 3 4 5])

Pol = x^4 + 2*x^3 + 3*x^2 + 4*x + 5;

>> v = roots(Pol)

v=

0.2878 + 1.4161i

0.2878 - 1.4161i -1. 2878 + 0. 8579i -1. 2878 - 0. 8579и

>> plot(Pol)

Результат представлен на рис. 3.2.

Чтобы получить перечень всех созданных методов класса, следует воспользоваться командой methods <имя класса>.

Например:

>> methods polynom

Рис. 3.2

Теперь мы имеем мощный вычислительный аппарат для работы с полиномами. Развивая его дальше, можно создать новый класс более сложных объектов - класс рациональных передаточных функций, которые являются конструкцией в виде дроби, числителем и знаменателем которой являются полиномы. Для этого класса также можно определить важные для инженера операции сложения передаточных функций (которое соответствует параллельному соединению звеньев с заданными передаточными функциями), умножения (ему соответствует последовательное соединение звеньев) и многие другие, отвечающие определенным типам соединений звеньев. Примерно на такой основе создан, к примеру, класс tf

(Transfer Function), используемый в пакете CONTROL.

5. Цифровая обработка сигналов

(пакет Signal Processing Toolbox)

Цифровая обработка сигналов традиционно включает в себя создание средств численного преобразования массива заданного (измеренного в дискретные моменты времени) процесса изменения некоторой непрерывной физической величины с целью извлечения из него полезной информации о другой физической величине, содержащейся в измеренном сигнале.

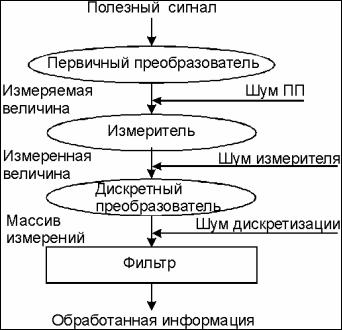
Общая схема образования измеряемого сигнала и процесса его преобразования в целях получения информаци о величине, которая должна быть измерена, представлена на рис. 5.1.

Рис. 5.1.

Физическая величина, являющаяся полезной (несущей в себе необходи-мую информацию), редко имеет такую физическую форму, что может быть непосредственно измеренной. Обычно она представляет лишь некоторую составляющую (сторону, часть, черту) некоторой другой физической величины, которая может быть непосредственно измерена. Связь между этими двумя величинами обозначим введением звена, которое назовем "первичным преобразователем" (ПП). Обычно закон преобразования известен заранее, иначе вос-становить информационную составляющую в дальнейшем было бы невозможным. Первичный преобразователь вносит зависимость сигнала, который может быть измерен, от некоторых других физических величин. Вследствие этого выходная его величина содержит, кроме полезной информа-ционной составляющей, другие, вредные составляющие или черты, искажа-ющие полезную информацию. И, хотя зависимость выхода ПП от этих других величин

также известна, однако вследствие неконтролируемого возможного изменения последних со временем, часто трудно спрогнозировать их влияние на искажение полезной составляющей. Назовем вносимую ПП вредную составляющую шумом ПП.

Пусть образованная таким образом непосредственно измеряемая величина измеряется некоторым измерителем. Любой реальный измеритель вносит собственные искажения в измеряемую величину и дополнительные зависимости от некоторых других физических величин, не являющихся объектом измерения. Назовем эти искажения шумами измерителя. Не ограничивая общности, будем полагать, что выходной величиной измерителя является электрический сигнал (измеренная величина), который можно в дальнейшем довольно просто пребразовывать электрическими устройствами.

Для осуществления цифровой обработки измеренная величина должна быть преобразована в дискретную форму при помощи специального устрой-ства,

которое содержит экстраполятор и аналого-цифровой преобразователь (АЦП).

Первый производит фиксацию отдельного текущего значения измерен-ной величины в отдельные моменты времени через определенный постоянный промежуток времени, называемый дискретом времени. Второй переводит это значение в цифровую форму, которая позволяет в дальнейшем осуществлять преобразования с помощью цифровых ЭВМ. Хотя оба устройства могут вносить при таких преобразованиях собственные искажения в выходной (дискретный) сигнал, однако ими обычно пренебрегают, так как в большинстве случаев эти дополнительные искажения значительно меньше шумов ПП и измерителя.

Чтобы на основе полученного дискретизированного сигнала получить полезный сигнал, нужно рассчитать и создать устройство (программу для ЭВМ), которое осуществляло бы такие преобразования входного дискретного во времени сигнала, чтобы на его выходе искажения, внесенные шумами ПП и измерителя были минимизированы в некотором смысле. Это устройство называют фильтром.

Вобщем случае создание (проектирование) фильтра является задачей неопределенной, которая конкретизируется лишь на основе предварительно полученных знаний о закономерности образования измеряемой величины (модели ПП), о модели образования измеренной величины из измеряемой (модели измерителя), о характеристиках изменения во времени вредных физических величин, влияющих на образование измеряемой и измеренной величин, и закономерностей их влияния на искажение полезной информации.

Так как модели ПП и измерителя могут быть весьма разнообразными, традиционно задачу фильтрации решают только для некоторых наиболее распространенных на практике видов таких моделей, чаще всего - для линейных моделей.

Вобщем случае процесс создания фильтра распадается на такие этапы:

- на основе априорной информации о моделях ПП и измерителя и о характеристиках шумов, а также о задачах, которые должен решать фильтр,