15. Якісна оцінка коефіцієнтів кореляції за шкалою Чеддока. Розподіл Фішера-Іейтса.

Для якісної оцінки коефіцієнтів кореляції застосовуються різні шкали, найбільш часто – шкала Чеддока. В залежності від значень коефіцієнта кореляції зв'язок може мати одну з оцінок

0,1-0,3 – слабкий;

0,3-0,5 – помітний;

0,5-0,7 – помірний;

0,7-0,9 – високий;

0,9-1,0 – вельми високий.

Варто відмітити, що величина коефіцієнта кореляції не є доказом того, що між ознаками, що досліджуються, є причинно-наслідковий зв'язок, а являє собою оцінку ступеня взаємної узгодженості в змінах ознак. Для того, щоб встановити причинно-наслідкову залежність необхідним є аналіз якісної природи явищ.

У зв'язку з випадковістю вибірки r може бути відмінно від нуля, навіть якщо між спостережуваними величинами немає кореляції. Отже, для перевірки гіпотези про відсутність кореляції, необхідно перевіряти, значимо чи r відрізняється від нуля. А для цього потрібно знати розподіл r як випадкової величини. Цей розподіл відомий, але, як і варто було очікувати, воно залежить від невідомого генерального коефіцієнта . Однак, якщо ми як нульову візьмемо гіпотезу, що = 0 (відсутність кореляції), то r-розподіл відповідний = 0, сильно спрощується і буде залежати тільки від обсягу вибірки. Його щільність має вигляд

(2.10)

r-Розподіл називають розподілом Фішера-Іейтса. Видно, що це симетричний відносно нуля унімодальний розподіл. У статистичних таблицях наведені квантилі цього розподілу для деяких рівнів значимості та ступенів свободи.

У припущенні, що генеральна кореляція = 0, інтервальна оцінка для r з довірчою ймовірністю р = 1 - , очевидно, дорівнює

.

Отже, якщо виявиться, що знайдений за вибіркою коефіцієнт r задовольняє нерівності

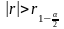(2.11)

то його потрібно визнати значущим, тобто потрібно вважати, що нульова гіпотеза невірна. А це означає, що   0 і між величинами, що спостерігаються, є кореляція. Вона буде тим сильніше, чим значніше | r | перевищує і наближається до 1.

16. Поняття кореляції. Оцінка значимості коефіцієнта кореляції з використанням t-критерію Стьюдента.

Если D(X + Y)  D(X) + D(Y), величины коррелированы

Сила кореляції визначається величиною яку з цієї причини називають кореляційним моментом або коваріацією. Отже, коваріація – це статистична міра взаємодії двох змінних. Очевидно, необхідною і достатньою умовою кореляції служить нерівність Кореляційний момент залежить від одиниць вимірювання величин X і Y, тому на практиці частіше використовується безрозмірна величина

(2.4)

яка називається коефіцієнтом кореляції.

Оцінка значимості коефіцієнта корреляції при малих обсягах вибірки виконується з використанням t-критерію Стьюдента. При цьому фактичне (спостережне) значення цього критерію визначається за формулою

. (2.12)

Розраховане за цією формулою значення порівнюється з критичним значенням t-критерію Стьюдента з урахуванням заданного рівня значущості та числа ступенів свободи n-2.

Якщо 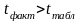, то отримане значення коефіцієнта кореляції признається значущим і робиться висновок про тісний статистичний взаємозв’язок величин.