23. Властивості оцінок параметрів регресійного рівняння: незміщеність, обґрунтованість, ефективність та інваріантність.

що останні не мають систематичної похибки (незміщеність), надійність їх підвищується зі збільшенням обсягу вибірки (обґрунтованість), вони є найкращими серед інших оцінок параметрів, лінійних відносно ендогенної змінної (ефективність). Крім того, оцінка перетворених параметрів (оцінка функції від параметра) може бути отримана в результаті аналогічного перетворення оцінки параметра (інваріантність).

24. Оцінки найменших квадратів. Верифікація моделі. Стандартна похибка рівняння. Оцінений коефіцієнт детермінації.

Метод найменших квадратів дає оцінки, що мають найменшу дисперсію в класі всіх лінійних оцінок, якщо виконуються передумови нормальної лінійної регресійної моделі. МНК мінімізує суму квадратів відхилень спостерігаємих значень від модельних значень .

(3.12)

Розв’язок системи нормальних рівнянь в матричній формі має вигляд

.

Для перевірки коректності побудови моделі визначають насамперед:

• стандартну похибку рівняння;

• коефіцієнт детермінації;

• коефіцієнт множинної кореляції;

• стандартну похибку параметрів.

Зауважимо, що зазначені показники отримують на підставі конкретних статистичних даних, тобто кожна з цих характеристик є вибірковою характеристикою і тому має бути перевірена на значущість за допомогою спеціальних статистичних критеріїв.

Стандартна похибка рівняння (точкова оцінка емпіричної дисперсії залишків) характеризує абсолютну величину розкиду випадкової складової рівняння і обчислюється за формулою

. (3.14)

Поправка на число ступенів свободи дає незміщену оцінку дисперсії залишків:

.

Коефіцієнт детермінації R² показує, яка частина руху залежної змінної описується даним регресійним рівнянням, і обчислюється за формулою

, (3.16)

де ; – середнє значення залежної змінної,

. (3.17)

На значення коефіцієнта детермінації впливає кількість факторів, що враховано в моделі. Уведення в модель кожної нової змінної збільшує значення коефіцієнта детермінації. Тому, щоб запобігти невиправданому розширенню моделі й мати змогу порівнювати моделі з різною кількістю факторів, уводять спеціальний оцінений коефіцієнт детермінації

, (3.18)

де – незміщена оцінка дисперсії залишків; – незміщена оцінка дисперсії залежної змінної, .

25. Оцінки найменших квадратів. Перевірка значущості та довірчі інтервали. Прогнозування за лінійною моделлю.

Метод найменших квадратів дає оцінки, що мають найменшу дисперсію в класі всіх лінійних оцінок, якщо виконуються передумови нормальної лінійної регресійної моделі. МНК мінімізує суму квадратів відхилень спостерігаємих значень від модельних значень .

(3.12)

Розв’язок системи нормальних рівнянь в матричній формі має вигляд

.

Для перевірки статистичної значущості коефіцієнта детермінації R² висувається нульова гіпотеза H₀ : R² = 0. Це означає, що досліджуване рівняння не пояснює змінювання регресанда під впливом відповідних регресорів. У такому разі всі коефіцієнти при незалежних змінних мають дорівнювати нулю. При цьому нульову гіпотезу можна подати у вигляді

(3.23)

Альтернативною до неї є H_A: значення хоча б одного параметра моделі відмінне від нуля, тобто хоча б один із факторів впливає на змінювання залежної змінної.

Для перевірки цих гіпотез застосовують F-критерій Фішера з m і n-m-1 ступенями свободи. За отриманими в моделі значеннями коефіцієнта детермінації R² обчислюють експериментальне значення F-статистики:

, (3.24)

яке порівнюють з табличним значенням розподілу Фішера при заданому рівні значущості α (як правило, α = 0,05 або α = 0,01). Якщо F_табл < F_експ, нульова гіпотеза відхиляється, тобто існує такий коефіцієнт у регресійному рівнянні, який суттєво відрізняється від нуля, а відповідний фактор впливає на досліджувану змінну Відхилення нуль-гіпотези свідчить про адекватність побудованої моделі. У протилежному випадку модель вважається неадекватною.

Коефіцієнт кореляції, як вибіркова характеристика, перевіряється на значущість за допомогою t-критерію Стьюдента. Фактичне значення t-статистики обчислюється за формулою

. (3.25)

і порівнюється з табличним значенням t-розподілу з n-m-1 ступенями свободи та при заданому рівні значущості α/2 (такий рівень зумовлений тим, що критична область складається з двох проміжків). Якщо абсолютна величина експериментального значення t-статистики перевищує табличне, тобто

, (3.26)

можна зробити висновок, що коефіцієнт кореляції достовірний (значущий), а зв’язок між залежною змінною та всіма незалежними факторами суттєвий.

Окрім загальних показників адекватності моделі існують також оцінки, що дають змогу встановити якість окремих частин рівняння, зокрема одного чи кількох коефіцієнтів регресії. Як і в попередніх випадках, рішення відносно якості коефіцієнтів приймають на основі відповідних статистичних критеріїв.

На підставі одного з найважливіших припущень МНК – припущення про нормальний розподіл випадкової складової рівняння з нульовим математичним сподіванням і сталою дисперсією – доведено, що кожний параметр лінійної регресії також має нормальний розподіл. Причому математичне сподівання параметра дорівнює значенню параметра узагальненої регресії, а дисперсія – незміщеній дисперсії випадкової складової рівняння, помноженій на відповідний діагональний елемент оберненої матриці .

Статистичну значущість кожного параметра моделі можна перевірити за допомогою t-критерію. При цьому нульова гіпотеза має вигляд

, (3.27)

альтернативна

. (3.28)

Експериментальне значення t-статистики для кожного параметра моделі обчислюється за формулою

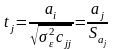(3.29)

де с_jj – діагональний елемент матриці ;

– стандартизована похибка оцінки параметра моделі, .

Експериментальне значення t_j-критерію порівнюється з табличним значенням t_табл з n-m-1 ступенями свободи при заданому рівні значущості α/2 (критична область розбивається на два фрагменти, межі яких задаються квантилем α/2). Якщо значення t_j-статистики потрапляє до критичної області (за абсолютним значенням перевищує t_табл), приймається альтернативна гіпотеза про значущість відповідного параметра. Інакше робиться висновок про статистичну незначущість параметра а_j, а це означає, що відповідна незалежна змінна не впливає суттєво на змінювання регресанда.

Оскільки t_j -статистика є відношенням відповідного параметра моделі до його стандартної похибки (середньоквадратичного відхилення), то на практиці частіше застосовують грубішу оцінку а саме допускають, щоб стандартні похибки становили 45-50 % значення параметра, аби стверджувати про його статистичну значущість.

Довірчі інтервали для кожного окремого параметра а_j обчислюються на основі його стандартної похибки та критерію Стьюдента:

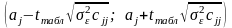. (3.30)

Табличне значення t_табл , як і раніше, має n-m-1 ступенів свободи і рівень значущості α/2 ( ).

Обчислені значення t_j-статистик застосовують також для розрахунку часткових коефіцієнтів детермінації , які визначають граничний внесок j-го регресора в загальний коефіцієнт детермінації. Коефіцієнт показує, на яку величину зменшиться коефіцієнт детермінації R², якщо j-ий регресор (і лише він!) буде вилучений з групи регресорів. Формула для розрахунку часткового коефіцієнта детермінації має вигляд

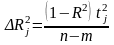. (3.31)

Часткові коефіцієнти детермінації і , обчислені за відповідними значеннями і , можуть бути як додатними, так і від’ємними, що дає змогу більш об’єктивно оцінювати моделі з різною кількістю регресорів.

Прогнозування за лінійною моделлю

Якщо побудована модель адекватна за F-критерієм, то її застосовують для прогнозування залежної змінної.

Про прогнозування регресанда говорять тоді, коли в часових рядах прогнозний період настає пізніше, ніж базовий. Якщо регресія побудована за просторовими даними, прогноз стосується тих елементів генеральної сукупності, що перебувають за межами застосованої вибірки.

Якість прогнозу тим краща, чим повніше виконуються передумови моделі в прогнозний часовий період, надійніше (вірогідніше) оцінено параметри моделі й більш точно визначено прогнозні значення регресорів.

Значення для майбутнього періоду чи додаткового елемента обчислюють за формулою (3.4)

за відомим вектором оцінених параметрів і за вектором значень незалежних змінних, що не належать до базового періоду. Розрізняють прогноз середній (оцінку математичного сподівання регресанда) та індивідуальний (оцінку певної реалізації регресанда , що відповідає моменту p). Перша з них базується на передумові МНК про нульове математичне сподівання випадкової складової рівняння регресії, а друга застосовує оцінене значення . Оцінену дисперсію прогнозу обчислюють відповідно за формулами

; (3.32)

. (3.33)

Зрозуміло, що здебільшого реальне значення показника y_t не збігатиметься зі значенням його математичного сподівання, але якщо розглядати велику кількість вибірок, на підставі яких визначатиметься прогноз, то можна гарантувати, що приблизно (1 - )100 % результатів потраплять відповідно до інтервалів

; (3.34)

, (3.35)

де t_α/2 – табличне значення критерію Стьюдента з n-m-1 ступенями свободи та при заданому рівні значущості α/2. (Значення α/2 вибирають, як і раніше, через двосторонні критичні межі.)

Очевидно, з віддаленням від середнього значення вибірки спостережень похибка прогнозу зростатиме, що призведе до збільшення довірчого інтервалу для індивідуального значення залежної змінної.