21. «Істинне» рівняння регресії. Парна регресія. Систематична та випадкова складові.

Після кореляційного аналізу проводиться регресійний аналіз, основною задачею якого є дослідження залежності змінної, що вивчається, від різних факторів та відображення їх взаємозв’язку у формі регресійної моделі.

Нехай маємо набір значень двох змінних  – пояснювальна змінна та  – пояснююча змінна, кожна з яких містить n спостережень. Нехай між ними теоретично існує деяка лінійна залежність

, (3.1)

Це рівняння будемо називати «істинним» рівнянням регресії.

Однак в дійсності між змінними спостерігається не настільки жорсткий зв'язок. Окремі спостереження будуть відхилятися від від лінійної залежності в силу різних причин. Враховуючи можливі відхилення лінійне рівняння зв’язку двох змінних (парну регресію) представимо у вигляді

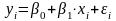, (3.2)

де  – постійна величина (або вільний член рівняння);

 – коефіцієнт регресії, що визначає нахил лінії. вздовж якої розсіяні дані спостереження;

 – випадкова змінна (випадкова складова, залишок або збурення).

Випадкова складова відображає той факт, що зміна буде неточно описуватися зміною , оскільки присутні інші фактори, невраховані в даній моделі. Таким чином в рівнянні (3.2) значення кожного спостереження представлено як сума двох частин – систематичної та випадкової . В свою чергу систематичну частину можна представити у вигляді рівняння

. (3.4)

Можна сказати, що загальним моментом для будь-якої економетричної моделі є розбиття залежної змінної на дві частини – пояснену та випадкову.

22. Умови Гаусса-Маркова.

1. Математичне сподівання випадкових відхилень повинно дорівнювати нулеві (незміщеність оцінок):

. (3.5)

Ця умова вимагає, щоб випадкові відхилення в середньому не впливали на залежну змінну Y, тобто в кожному конкретному спостереженні відхилення може набувати додатні або від’ємні значення, але не повинно спостерігатися систематичне зміщення відхилень в переважній більшості в бік одного знаку.

Із врахуванням вищесказаного, використовуючи рівняння (3.2), будемо мати:

(3.6)

2. Дисперсія випадкових відхилень повинна бути сталою величиною

, . (3.7)

Ця вимога передбачає, що не зважаючи на те, що при кожному конкретному спостереженні випадкове відхилення може виявитися відносно великим чи малим, це не повинно складати основу для апріорної причини, тобто причини, що не базується на досвіді, що спонукала б велику похибку.

Моделі, для яких виконується умова (3.7), називають гомоскедастичними (рівнозмінними). Моделі, для яких не виконується умова (2) ( ), називають гетероскедастичними.

Величина , звичайно, не відома і одна з задач регресійного аналізу полягає в оцінці стандартного відхилення випадкової складової.

3. Випадкові відхилення та , повинні бути незалежними одне від одного.

Виконання цієї умови припускає, що між будь-якими випадковими відхиленнями відсутній систематичний зв’язок, тобто величина та знак будь-якого випадкового відхилення не буде являтися причиною величини та знаку будь-якого іншого випадкового відхилення. Цю умову можна записати так

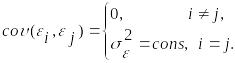(3.8)

Тут є математичний запис коваріаційного (кореляційного) моменту.

4. Випадковий вектор відхилень повинен бути незалежним від регресорів матриці .

Ця умова виконується автоматично, коли пояснюючі змінні не є стохастичними величинами в заданій моделі.

Наявність таких властивостей оцінок гарантує, що останні не мають систематичної похибки (незміщеність), надійність їх підвищується зі збільшенням обсягу вибірки (обґрунтованість), вони є найкращими серед інших оцінок параметрів, лінійних відносно ендогенної змінної (ефективність). Крім того, оцінка перетворених параметрів (оцінка функції від параметра) може бути отримана в результаті аналогічного перетворення оцінки параметра (інваріантність).