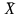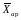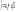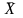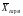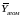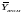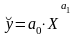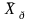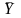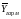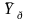- •Загальні поняття економетричних моделей. Задачі економетрії.
- •Кореляційно-регресійний аналіз в економіці. Функціональний та кореляційний зв’язки.
- •2) Визначення тісноти зв'язку (задача кореляційного аналізу).
- •Функція регресії. Регресор. Регресат. Причини обов'язкової присутності в регресійних моделях випадкового фактора.
- •Просторові дані. Часові ряди. Особливості часових рядів. Кореляційне поле.
- •Застосування методу Фостера-Стюарта з метою виявлення закономірного зв’язку між змінними
- •Методи вибору найкращої функції регресії
- •Економетрична модель. Специфікація моделі регресії.
- •Економетрична модель. Параметризація рівняння регресії.
- •Моделі часових рядів. Регресійні моделі з одним рівнянням.
- •Моделі часових рядів. Системи незалежних, рекурсивних, взаємозалежних рівнянь.
- •Порівнянність та однорідність даних. Повнота даних та стійкість.
- •Сутність методу найменших квадратів
- •Застосування методу максимальної правдоподібності з метою оцінювання параметрів економетричної моделі
- •Поняття кореляція. Кореляційний момент або коваріація. Коефіцієнт кореляції. Вибірковий кореляційний момент. Стандартна похибка.
- •Якісна оцінка коефіцієнтів кореляції за шкалою Чеддока. Розподіл Фішера-Іейтса.
- •Поняття кореляції. Оцінка значимості коефіцієнта кореляції з використанням t-критерію Стьюдента.
- •Матриця коефіцієнтів парної кореляції. Вибірковий коефіцієнт множинної кореляції та коефіцієнт детермінації. Вибірковий частинний коефіцієнт кореляції.
- •Проблема мультиколінеарності. Застосування алгоритму Фаррера-Глобера.
- •Індекс кореляції. Методика розрахунку кореляційного відношення.
- •Побудова економетричної моделі на основі покрокової регресії.
- •«Істинне» рівняння регресії. Парна регресія. Систематична та випадкова складові.
- •Умови Гаусса-Маркова.
- •Властивості оцінок параметрів регресійного рівняння: незміщеність, обґрунтованість, ефективність та інваріантність.
- •Оцінки найменших квадратів. Верифікація моделі. Стандартна похибка рівняння. Оцінений коефіцієнт детермінації.
- •Оцінки найменших квадратів. Перевірка значущості та довірчі інтервали. Прогнозування за лінійною моделлю.
- •Множинна регресія. Специфікація багатофакторної моделі. Помилки специфікації множинної регресії.
- •Мультиколінеарність. Практичні наслідки мультиколінеарності та методи її усунення.
- •Оцінка якості моделі множинної регресії. Перевірка виконання передумов мнк. Перевірка гіпотези про нормальний розподіл залишків регресії
- •Етапи побудови економетричної моделі.
- •Оцінка якості прогнозів за регресійними моделями
- •Нелінійна регресія відносно пояснюючих змінних. Нелінійна регресія по параметрам, що оцінюються. Внутрішньо лінійна та нелінійна функції.
- •Особливості параметризації нелінійної регресії. Вибір аналітичної форми дослідження.
- •Фіктивні змінні. Ілюстрація використання фіктивної змінної. Множинні сукупності фіктивних змінних.
- •Оцінка якості моделі. Дослідження відповідності моделі емпіричним даним. Оцінка точності моделі.
- •Поняття гомоскедастичності та гетероскедастичності залишків. Наслідки порушень припущення про гомоскедастичність.
- •Методи виявлення гетероскедастичності. Тест Голдфельда-Квандта. Тест рангової кореляції Спірмена.
- •Трансформування початкової моделі з гетероскедастичністю.
- •Зважений метод найменших квадратів.
- •Оцінювання параметрів регресії за допомогою узагальненого методу найменших квадратів (методу Ейткена).
- •Поняття автокореляції. Автокореляція залишків. Лагові затримки.
- •Природа автокореляції та її наслідки. Методи усунення автокореляції.
- •Тестування наявності автокореляції. Критерій Дарбіна-Уотсона. Критерій фон Неймана.
- •Коефіцієнти автокореляції та їх застосування. Автокореляційна функція та корелограма.
- •Оцінка параметрів моделі з автокорельованими залишками. Метод Ейткена.
- •Оцінка параметрів моделі з автокорельованими залишками. Метод Кочрена-Оркатта.
- •Прогноз на основі моделі з автокорельованими залишками.
- •Узагальнені економетричні моделі.
- •Поняття лагу і лагових змінних.
- •Дистрибутивно-лагові моделі. Авторегресійні моделі.
- •Моделі розподіленого лагу. Узагальнена модель розподіленого лагу.
- •Оцінка параметрів лагових моделей. Метод послідовного збільшення кількості лагів.
- •Перетворення Койка (метод геометричної прогресії).
- •Модель адаптивних сподівань. Модель часткового коригування.
- •Оцінювання параметрів методом Ейткена.
- •Динамічний та часовий ряди. Систематичні та випадкові компоненти часового ряду. Стаціонарність часового ряду.
- •Фільтрація компонент часового ряду. Ts, ds, тренд-сезонні, нелінійні часові ряди.
- •Дослідження автокореляційної функції часового ряду.
- •Методи фільтрації сезонної компоненти.
- •Прогнозування тенденції часового ряду за механічними методами та аналітичними методами.
- •Адаптивні методи прогнозування.
- •Метод декомпозиції часового ряду. Розрахунок сезонної хвилі.
- •Системи одночасних економетричних рівнянь. Ендогенні та екзогенні змінні.
- •Структурна та зведена форми економетричної моделі. Повна економетрична модель.
- •Ідентифікованість моделі. Необхідна та достатня умови ідентифікованості системи.
- •Непрямий метод найменших квадратів.
- •Двокроковий та трикроковий методи найменших квадратів.
- •Прогноз ендогенних змінних і загальні довірчі інтервали.
Застосування методу Фостера-Стюарта з метою виявлення закономірного зв’язку між змінними
Наиболее распространенным из них является метод Фостера - Стюарта. Он позволяет не только установить наличие тенден-ции в связи количественных признаков Y и X, но и проверить гипотезу (1.17) о постоянстве дисперсии случайного возмуще-ния. Сущность метода заключается в следующем.
Сравнивается каждый уровень ряда со всеми предыдущими, при этом
fi = 1, ei = 0, если Yi > Yk , k=1, 2,..., i-1;
fi = 0, ei = 1, если Yi < Yk , k=1, 2,..., i-1;
fi = 0, ei = 0 в остальных случаях.
2 Вычисляются значения величин
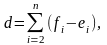
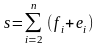 .
.
Показатели d
и s
характеризуют тенденции в связях Y
и X
и дисперсии
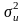 и Х
соответственно.
и Х
соответственно.
3 С помощью
t-критерия
Стьюдента проверяется гипотеза о том,
можно ли считать случайными разности
d
- 0
и
 .
C
этой целью
находятся величины
.
C
этой целью
находятся величины

 (1.22)
(1.22)
где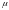 - среднее
значение величины s;
- среднее
значение величины s;
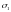 и
и
 - стандартные ошибки величин d
и
s
соответственно. Значения величин
,
и
табулированы
и приведены в табл. 1.2.
- стандартные ошибки величин d
и
s
соответственно. Значения величин
,
и
табулированы
и приведены в табл. 1.2.
4 При заданном
уровне
 сравниваются
расчетные значения
td
и ts
c
табличным.
Если td
<
tтабл
и ts
<
tтабл
, то гипотеза
об отсутствии тенденций в связи Y
и
X,
и
и
Х
подтверждается.
сравниваются
расчетные значения
td
и ts
c
табличным.
Если td
<
tтабл
и ts
<
tтабл
, то гипотеза
об отсутствии тенденций в связи Y
и
X,
и
и
Х
подтверждается.
Методи вибору найкращої функції регресії
При моделировании монотонных процессов(возрастающих или убывающих) , когда число наблюдений n невелико и неясно, есть ли асимптотический уровень и перегиб в тенденции изменения результативной переменной Y c ростом объясняющей переменной Х может быть использована одна из следующих функций регрессии, зависящих от двух параметров:
а)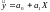 ,
б)
,
б)
 ,
в)
,
в)
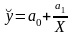 ,
,
г)
 ,
д)
,
д)
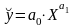 ,
е)
,
е)
 ,
,
ж)
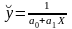 ,
з)
,
з)
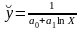 ,
и)
,
и)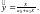
Первые производные
этих функций при
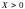 имеют постоянный знак и, следовательно,
сами функции либо возрастают, либо
убывают при положительных Х
(в зависимости от значения параметров).
имеют постоянный знак и, следовательно,
сами функции либо возрастают, либо
убывают при положительных Х
(в зависимости от значения параметров).
Приведенные девять
зависимостей примечательны тем, что
если все табличные точки (Хі,
Yi)
удовлетворяют
одному из этих уравнений, то и средние
значения
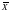 и
и
 также
ему удовлетво-ряют. При этом в качестве
средних значений
и
могут
быть средние арифметические, средние
геометрические или средние гармонические.
Вспомним, что среднее арифметическое
n
положительных
чисел Z1,
Z2,...,
Zn
определяется по формуле
также
ему удовлетво-ряют. При этом в качестве
средних значений
и
могут
быть средние арифметические, средние
геометрические или средние гармонические.
Вспомним, что среднее арифметическое
n
положительных
чисел Z1,
Z2,...,
Zn
определяется по формуле
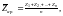
среднее геометрическое есть величина, равная
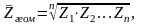
среднее гармоническое
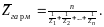
Характерные средние и для каждой из девяти возможных функций приведены в таблице 1.5.
Т а б л и ц а 1.5 - Характерные средние для монотонных функций
|
|
|
Вид эмпирической функции |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
Для проверки
пригодности выбранной эмпирической
функции, используя исходные
данные
табл, находят значения
и
 Затем сравнивают Yі,
соответствующее исходным данным, со
значением
Затем сравнивают Yі,
соответствующее исходным данным, со
значением
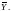 Если
не находится среди исходных данных Хі,
то соответствующее значение Y
можно определить с помощью линейной
интерполяции, проведя через точки (Хі,
Yі
), (Хi+1,
Yi+1)
прямую.
Здесь Хі
и Хі+1
- промежуточные значения, между которыми
содержится
Если
не находится среди исходных данных Хі,
то соответствующее значение Y
можно определить с помощью линейной
интерполяции, проведя через точки (Хі,
Yі
), (Хi+1,
Yi+1)
прямую.
Здесь Хі
и Хі+1
- промежуточные значения, между которыми
содержится
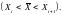 Из уравнения
прямой получаем
Из уравнения
прямой получаем
 В качестве критерия выбора наилучшей
функциональной зависимости можно
выбрать следующий:
В качестве критерия выбора наилучшей
функциональной зависимости можно
выбрать следующий:
 .
.
+про корр.поле рассказать