38. Трансформування початкової моделі з гетероскедастичністю.

Трансформація моделі зводиться до зміни початкової форми моделі методом, який залежить від специфічної форми гетероскедастичності. тобто від форми залежності між дисперсіями залишків і значеннями незалежних змінних

Припустимо, що гетероскедастичність має форму:

.

Трансформація початкової моделі здійснюється діленням іі на .

Зазначимо, що така трансформація еквівалентна застосуванню зваженого методу найменших квадратів

ЗМНК, застосований до початкової моделі дає такі ж результати, що і застосування МНК до трансформованої моделі.

Оцінки трансформованої модлеі мають меншу дисперсію (ефективніші) ніж оцінки, отримані із застосуванням МНК до початкової моделі.

39. Зважений метод найменших квадратів.

В 2х словах: сначала оцениваем по МНК, потом проводим трансформацию(38 вопрос)

(ЗМНК), який є особливим випадком узагальненого методу найменших квадратів (УМНК). Суть ЗМНК полягає в мінімізації зваженої суми квадратичних відхилень

Пусть на первом этапе оценена линейная регрессионная модель с помощью обычного МНК. Предположим, что остатки е_i независимы между собой, но имеют разные дисперсии (поскольку теоретические отклонения е_i нельзя рассчитать, их обычно заменяют на фактические отклонения зависимой переменной от линии регрессии ^., для которых формулируются те же исходные требования, что и для є_i). В этом случае квадратную матрицу ковариаций cov(e_i, e_j) можно представить в виде:

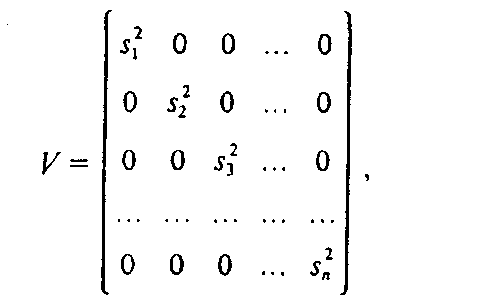
где cov(e_i, e_j)=0 при i  j; cov(e_i, e_j)=S²; п - длина рассматриваемого временного ряда.

Если величины известны, то далее можно применить взвешенный МНК, используя в качестве весов величины и минимизируя сумму

40. Оцінювання параметрів регресії за допомогою узагальненого методу найменших квадратів (методу Ейткена).

За наявності гетероскедастичності для оцінювання параметрів моделі доцільно застосовувати узагальнений метод найменших квадратів (метод Ейткена), вектор оцінювання якого має вигляд:

.

Вектор а містить незміщену лінійну оцінку параметрів моделі, яка має найменшу дисперсію і матрицю коваріацій:

.

Для отримання УМНК-оцінок необхідно знати коваріаційну матрицю S вектора похибок, яка на практиці дуже рідко відома. Тому природно спершу оцінити матрицю S, а потім застосувати її оцінку у формулах. Цей підхід є суттю УМНК.

Оскільки явище гетероскедастичності пов’язане лише з тим, що змінюються дисперсії залишків, а коваріація між ними відсутня, то матриця S має бути діагональною, а саме:

Звідси в матриці S значення можна обчислити, користуючись гіпотезами:

а) , тобто дисперсія залишків пропорційна до зміни пояснювальної змінної ;

б) , тобто зміна дисперсії пропорційна до зміни квадрата пояснювальної змінної ( );

в) , тобто дисперсія залишків пропорційна до зміни квадрата залишків за модулем.

Для першої гіпотези:

Для другої гіпотези:

Для третьої гіпотези:

41. Поняття автокореляції. Автокореляція залишків. Лагові затримки.

7.1 Природа автокореляції та її наслідки

Автокореляція – це взаємозв’язок послідовних елементів часового чи просторового ряду даних.

В економетричних дослідженнях часто зустрічаються такі випадки, коли дисперсія залишків є постійною, але спостерігається їх коваріація. Це явище має назву автокореляції залишків. В економетричних моделях автокореляція залишків має особливе значення, оскільки при її наявності порушується одна з умов, що висуваються при оцінці параметрів моделі за методом 1МНК.

Автокореляція залишків виникає найчастіше тоді, коли економетрична модель будується на основі часових рядів. Якщо існує кореляція між послідовними значеннями деякої незалежної змінної, то спостерігатиметься й кореляція послідовних значень залишків, так звані лагові затримки (запізнювання) в економічних процесах.

Тобто в цьому випадку також порушується гіпотеза, згідно з якою але при гетероскедастичності змінюється дисперсія залишків при відсутності їх коваріації, а при автокореляції – існує коваріація залишків при незмінній дисперсії.

При автокореляції залишків, як і при гетероскедастичності дисперсія залишків запишеться:

(7.1)

але матриця матиме тут зовсім інший вигляд. Запишемо цю матрицю:

. (7.2)

В даній матриці параметр  характеризує коваріацію кожного наступного значення залишків із попереднім. Так, якщо для залишків записати авторегресійну модель першого порядку:

, (7.3)

то  характеризує силу зв’язку величини залишків у період t від величини залишків у період t – 1.

Якщо проігнорувати матрицю при визначенні дисперсії залишків, і для оцінки параметрів моделі застосувати метод 1МНК, то можливі такі наслідки:

1) оцінки параметрів моделі можуть бути незміщеними, але неефективними, тобто вибіркові дисперсії вектора оцінок можуть бути невиправдано великими;

2) статистичні критерії t і F- статистики, які отримані для класичної лінійної моделі, практично не можуть бути використані для дисперсійного аналізу, бо їх розрахунок не враховує наявності коваріації залишків;

3) неефективність оцінок параметрів економетричної моделі, як правило, призводить до неефективних прогнозів, тобто прогнозні значення матимуть велику вибіркову дисперсію.

Автокореляція може виникати через інерційність і циклічність багатьох економічних процесів. Провокувати автокореляцію також може неправильно специфікована функціональна залежність у регресійних моделях. Наприклад, модель може не включати істотній фактор, яким часто виступає фактор часу.

При чому важливо відрізняти від істинної автокореляції залишків випадки неправильної специфікації моделі. Оскільки в останньому випадку необхідно змінити форму моделі. При цьому можуть використовуватися різні методи усунення автокореляції, наприклад:

• введення у модель фактору часу;

• перехід до темпових чи відносних показників;

• включення у модель неврахованих факторів;

• побудова авто регресійних рівнянь.

У випадку ж істинної автокореляції залишків застосовують спеціальні методи оцінки параметрів регресії з автокорельованими залишками.