20. Группа подстановок.

Теорема Силова. Если порядок конечной группы делится на степень p^r простого числа p, то эта группа имеет подгруппу порядка p^r.

Силовская подгруппа. Если  G = p^k s и s не делится на p, то подгруппы порядка p^k группы G называются силовскими p-подгруппами.

Следствие 1. Если порядок конечной группы делится на простое число p, то в группе имеется элемент порядка p.

Следствие 2. Порядок любой конечной p-группы является степенью числа p.

Основная теорема об абелевых группах. Любая конечная абелева группа разлагается в прямое произведение циклических групп, порядки которых являются степенями простых чисел; множество степеней простых чисел, являющихся порядками указанных групп, однозначно определяется порядком самой группы.

Это надо понимать следующим образом: если , то можно указать такие циклические группы A₁, A₂, . . . , A_k порядков , соответственно, что . Отсюда следует, что конечная абелева группа однозначно определяется с точностью до изоморфизма конечным набором степеней простых чисел.

Пусть даны множество H = {1, 2, . . . , n} и группа подстановок  этого множества. Стабилизатором элемента x  H называется следующая подгруппа группы :

_x = {    x^ = x}

Орбитой элемента x относительно группы  называется множество x^ = { x^   }. В обоих случаях через x^  обозначается элемент, в который подстановка  переводит x.

Группа подстановок  множества H называется регулярной, если для каждого x  H имеет место _x = 1.

21. Иерархия систем с двумя бинарными операциями. Кольцо. Тело. Поле (коммутативное тело). Поле Галуа.

Кольцом называется непустое множество R, для элементов которого определены две бинарные операции — сложение и умножение (обозначаемые + и × соответственно; знак × обычно опускается), причем предполагаются выполненными следующие аксиомы колец (a, b, c Î R):

• Коммутативность сложения: a + b = b + a.

• Ассоциативость сложения:

• a + (b + c) = (a + b) + c.

• Обратимость сложения (возможность вычитания): уравнение a + x = b имеет решение x = b - a  Î R.

•  Дистрибутивность умножения относительно сложения:

a (b + c) = a b + a c и (b + c) a = b a + c a.

• Если 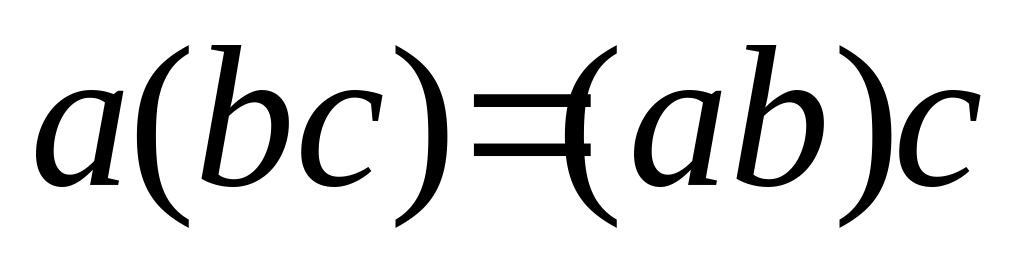, то кольцо называют ассоциативным;

• если 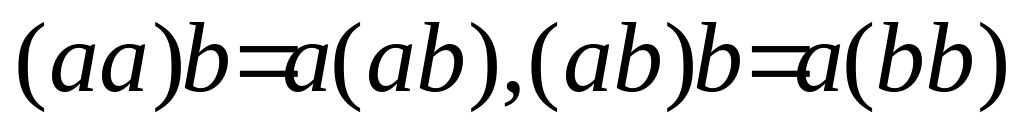, альтернативным;

• если ab = ba и 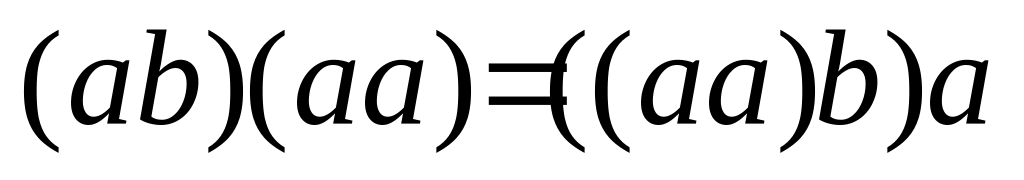, йордановым;

• если a2 = a, a(bc) + b(ca) +c(ab) = 0, то оно называется кольцом Ли;

• если ab = ba , то кольцо называется коммутативным.

Примеры колец:

множество всех целых чисел;

множество всех четных чисел и вообще целых чисел, кратных данному числу m;

множество всех рациональных чисел;

множество всех многочленов от одного или нескольких переменных с рациональными, действительными или комплексными коэффициентами;

множество всех функций, непрерывных на данном отрезке числовой прямой

• Тело есть такая система (A, + , ×), что система (A, +) является абелевой группой, а система (A¢, ×), где A¢ получается из A удалением нулевого элемента (т.е. нейтрального элемента абелевой группы), является группой и операция × дистрибутивна относительно операции + .

• Теорема. Кольцо является телом тогда и только тогда, когда оно содержит не менее двух элементов и оба уравнения ax = b и xa = b, разрешимы для любых элементов a, bΠA, где a ¹ 0.

• Тело служит обобщением системы (Q, + , ×) рациональных чисел, однако требование коммутативности умножения опускается.

• Теорема Веддербёрна Всякое конечное тело коммутативно.

• Поле может быть определено как множество, содержащее не менее двух элементов, на котором заданы две бинарные алгебраические операции — сложение и умножение, обе ассоциативные и коммутативные, связанные между собой законом дистрибутивности, т.е. для любых a, b, c из поля справедливо:

a + b = b + a , ab = ba ,

(a + b) + c = a + (b + c), (ab) c = a (bc),

(a + b) c = ac  + bc .

Кроме того, в поле требуется существование нулевого элемента 0 (нуля), для которого 0 + a = a , и для каждого элемента a противоположного элемента –a, то есть такого элемента, что a + (–a ) = 0, а также существование единичного элемента e (единицы), для которого ae = a, и для каждого ненулевого элемента a существование обратного элемента a–1, т.е. такого элемента, что aa–1 = e. Отсюда следует, что в поле выполнимы операция вычитания, а также операция деления на ненулевой элемент. Таким образом, все элементы поля образуют абелеву группу по сложению (аддитивная группа поля), а все ненулевые элементы — абелеву группу по умножению (мультипликативная группа поля).