27. Виды графов: двудольные графы, регулярные графы, полные графы, деревья, планарные графы

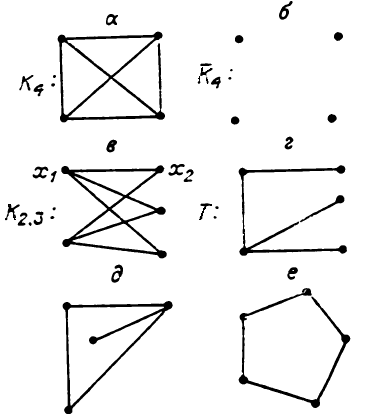
а — полный граф

б — пустой граф

в — полный двудольный граф

г — дерево

д — планарный граф

е — регулярный граф

28. Изоморфизм графов.

Два графа G(V, E) и H(W, I) называются изоморфными, если существует взаимно-однозначное соответствие между множествами вершин V, W и множествами ребер E, I, сохраняющее отношение инцидентности.

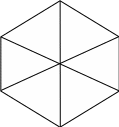
Вид матриц, также как списков рёбер зависит от нумерации вершин и рёбер графа. В связи с этим возникает весьма существенный вопрос о том, как определять равенство графов.

Строго говоря, граф считается полностью заданным, если нумерация его вершин зафиксирована. Графы, отличающиеся только нумерацией вершин, называются изоморфными.

Перенумерация вершин графа задаётся строкой новых номеров вершин, расположенных в исходном порядке. Новая матрица смежности получается из исходной матрицы перемещением каждого элемента в строку, в столбец. Поэтому, чтобы узнать, представляют ли две таблицы смежности изоморфные графы, можно, например, перевести всевозможные одинаковые перестановки строк и столбцов первой матрицы. Если одна из таких перестановок даст матрицу, тожественно совпадающую со второй матрицей, то представляемые ими графы изоморфны. Однако эта процедура может оказаться очень трудоёмкой, так как всего возможно выполнение перестановок.

29. Способы задания графов.

Каждый граф можно представить в евклидовом пространстве множеством точек, соответствующих вершинам, которые соединены линиями, соответствующими ребрам (или дугам — в последнем случае направление обычно указывается стрелочками). — такое представление называется укладкой графа.

Доказано, что в 3-мерном пространстве любой граф можно представить в виде укладки таким образом, что линии, соответствующие ребрам (дугам) не будут пересекаться во внутренних точках. Для 2-мерного пространства это, вообще говоря, неверно. Допускают представление в виде укладки в 2-мерном пространстве графы, называемые плоскими.

Существуют и другие способы задания графов. Пусть v₁, v₂, ... v_n — вершины графа G(V, E), а e₁, e₂, ... e_m — его ребра (дуги).

Матрицей смежности графа G называется матрица A=||a_ij||, i=1,...,n; j = 1, ..., n, у которой элемент a_ij равен числу ребер (или дуг), соединяющих вершины v_i и v_j (соответственно, идущих из вершины v_i в вершину v_j).

Матрицей инцидентности графа G называется матрица B=||b_ij||, i=1, .., n; j = 1, ..., m, у которой элемент b_ij равен 1, если вершина v_i инцидентна ребру (дуге) e_j и равен 0, если не инцидентна.

Наконец, граф можно задать посредством списков. Например,

вариант 1: списком пар вершин, соединенных ребрами (или дугами);

вариант 2: списком списков для каждой вершины множества смежных с ней вершин.

0-граф

Графическое представление

1) A  2) A   B 3) A   B

 C

4) A   B 5) A   B

C   D C   D

 E

Матрица смежности (квадратная!)

1)		A	2)		A	B
	A	0		A	0	0
				B	0	0

и так далее.

Матрица инцидентности (прямоугольная!)

1)		AA	2)		AA	AB	BA	BB
	A	0		A	0	0	0	0
				B	0	0	0	0

и так далее.

Список пар вершин (соответствие)

1)  2)  и так далее.

Список списков смежных вершин (простых поддеревьев)

1) A ( ) 2) A ( ), B ( ) и так далее.

1-граф

Варианты (с петлями, без петель, дуги, ребра и т.п.)

Графическое представление

1) A  2) а) A   B

4 ) б) A   B 5) A   B

и так далее.

Матрица смежности

1)		A	2) а)		A	B
	A	1		A	1	0
				B	0	0

2) б)		A	В	2) в)		A	B
	A	0	1		A	0	0
	В	0	0		B	0	1

и так далее.

Матрица инцидентности

1)		AA	2)		AA	AB	BA	BB
	A	1		A	1	0	0	0
				B	0	0	0	0

и так далее.

Список пар вершин

1) (A, A) 2) a) (A, A) 2) б) (A, В) и так далее.

Список списков смежных вершин

1) A (A) 2) а) A (A) 2) б) A (B) 2) в) B (B) и так далее.

30. Подграфы. Маршрут, цепь, простая цепь, (простой) цикл. Компонента связности. Связность в ориентированном графе. Дерево. Остовное дерево. Реберная и вершинная связности графа.

Орграф D называется сильно связным (сильным, категории связности 3), если для каждой пары вершин ui и uj в D ui достижима из uj и ui достижима из ui. Орграф D называется слабо связным (слабым, категории связности 1), если каждая пара вершин ui и uj в D соединима (полупутем). Орграф D называется односторонне связным (односторонним, категории связности 2), если для каждой пары вершин ui и uj в D либо ui достижима из uj , либо uj достижима из ui. Подграфом в D называется орграф (W, B), в котором W Í V, B Í A. Порожденным подграфом в D называется подграф (W, B), в котором B содержит все дуги из A, соединяющие вершины в W. Сильной компонентой в D называется максимальный сильно связный (порожденный) подграф.

Граф G называется связным, если каждая пара вершин ui и uj в G связана цепью. Аналогия — см. выше Аналогия — см. выше Подграфом в G называется граф (W, F), в котором W Í V, F Í E. Порожденным подграфом в G называется подграф (W, F), в котором F содержит все ребра из E, соединяющие вершины в W. Компонентой (связности) в G называется максимальный связный (порожденный) подграф.

Деревья

Граф G = <V, E> называется деревом, если он связен и ацикличен.

Пусть G = <V, E> — граф с n вершинами и m ребрами.

Необходимые и достаточные условия того, что G — дерево:

• Любая пара вершин в G соединена единственным путем

• G связен и m = n – 1

• G связен и удаление хотя бы одного его ребра нарушает связность графа

• G ацикличен, но если добавить хотя бы одно ребро, то в G появится цикл.

Остовной граф

• В любом связном графе найдется подграф, являющийся деревом.

• Подграф в G, являющийся деревом и включающий в себя все вершины G, называется остовным деревом.

• Построение остовного дерева: Выбираем произвольное ребро и последовательно добавляем другие ребра, не создавая при этом циклов, до тех пор, пока нельзя будет добавить никакого ребра, не получив при этом цикла.

• Всего n -1 ребро!!!

31. Обход графа. Длина маршрута, расстояние между вершинами. Одноместные операции: удаление или добавление ребра или вершины, стягивание ребра (отождествление пары смежных вершин), подразбиение ребра. Двухместные операции.

Граф — множество V вершин и набор E неупорядоченных и упорядоченных пар вершин; обычно граф обозначают как G(V, E).

Пусть G(V, Е) – неориентированный граф. Рассмотрим конечную последовательность рёбер такую, что любые два соседние ребра имеют одну общую инцидентную вершину . Эту последовательность называется маршрутом графа.

Маршрутом (путем) для графа G(V, Е) называется последовательность v₁e₁v₂e₂v₃…e_kv_k+1. Маршрут называется замкнутым, если его начальная и конечная точки совпадают. Число ребер (дуг) маршрута (пути) графа называется длиной маршрута (пути).

Любой отрезок конечного или бесконечного маршрута вида , где также является маршрутом и называется участком маршрута .

Заметим, что одно и то же ребро может встречаться не один раз. Вершина , инцидентная первому ребру маршрута и не инцидентная следующему ребру , называется началом маршрута. Причём если эти рёбра кратные, то необходимо указать, какая именно из двух инцидентных им вершин является началом маршрута. Аналогично определяется конец маршрута. Вершины, инцидентные рёбрам маршрута, за исключением первой и последней, называются промежуточными. Причём, поскольку одной вершине может быть инцидентно несколько рёбер, начало и конец маршрута могут быть в то же время промежуточными точками. Таков, например, маршрут на рисунке 1, где вершина 1 является началом маршрута и, в то же время, промежуточной точкой.

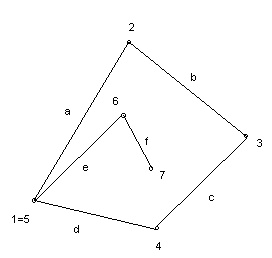
Рис 1.

Рассмотрим случай, когда , то есть начало и конец маршрута совпадают. Отметим, что в этом случае маршрут может быть только конечным..

Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью.

В простой цепи любая вершина маршрута инцидентна не более чем двум его рёбрам.

Замкнутый маршрут (путь) называется циклическим маршрутом или циклом (контуром). Цикл, в котором все вершины попарно различны, называется простым циклом.

Иначе говоря, простой цикл – это циклический маршрут, в котором любые два соседние ребра имеют одну инцидентную вершину. Последовательности , и представляют один и тот же цикл (рисунок 2). Часто считается, что можно менять порядок рёбер цикла на противоположный, то есть, например, последовательность представляет тот же цикл.

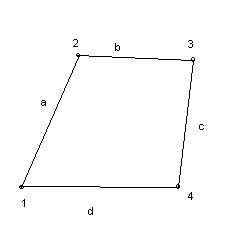
Рис2.

Участок цепи или цикла является цепью; соответственно, участок простой цепи или простого цикла является простой цепью.

Пусть связный неориентированный граф, любые две его вершины. Тогда существует связывающая их простая цепь . Если количество этих рёбер - не минимальное из возможных, существует цепь , причём .

Штрихи в обозначении используются, потому что не обязательно рёбра под одинаковыми индексами будут совпадать.

Если же и не минимально, то найдётся связывающая эти вершины цепь с ещё меньшим количеством рёбер и так далее. Однако этот процесс не бесконечен, его можно повторить не более, чем раз. Тогда существует цепь , связывающая вершины и с минимальным количеством рёбер .

Опр. Минимальная длина простой цепи с началом в вершине и концом в вершине называется расстоянием между этими вершинами. Обозначается: .

Расстояние между любой вершиной и ею самой равно 0. Ему соответствует нулевой маршрут, не содержащий рёбер. Для любой пары различных вершин и выполняется , так как связывающая их цепь состоит хотя бы из одного ребра. Вообще, расстояние удовлетворяет аксиомам метрики:

1) , причём тогда и только тогда, когда ;

2) .

Также для расстояния выполняется неравенство треугольника: для любых трёх вершин выполняется неравенство: .

Это позволяет, для простоты рассуждений, измерять расстояние между вершинами по числу рёбер простой цепи, соединяющей их (тем более, что геометрические характеристики рёбер мы не учитываем).

Опр. Диаметром конечного графа называется наибольшее из расстояний между парой его вершин: .

Кратчайшие простые цепи, связывающие две вершины графа с максимальным расстоянием между ними, называются диаметральными простыми цепями.

Пусть - рассматриваемая вершина данного графа, а произвольная вершина графа. Максимальным удалением в графе от фиксированной вершины называется величина .