32. Эйлеров путь в графе. Задача о кенигсбергских мостах. Эйлеров цикл. Теорема о существовании эйлерова цикла.
Цепь (цикл) в графе G называется Эйлеровым, если она проходит по одному разу через каждое ребро графа G.
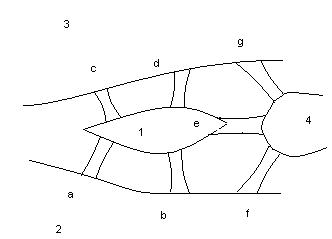
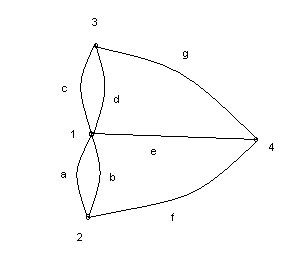
Задача, которая привела к появлению понятия Эйлерова цикла, широко известна в истории математики. Это так называемая задача о кенигсбергских мостах. Расположение семи мостов в городе Кенигсберге в начале XVIII века приведено на рисунке 3а. Требуется обойти город, пройдя через каждый мост ровно один раз, и вернуться в исходную точку.
Можно представить описанную задачу следующим образом. Имеется связный неориентированный граф с четырьмя вершинами и семью рёбрами. Требуется выяснить, существует ли простой цикл, позволяющий обойти данный граф по маршруту, включающему в себя по одному разу каждое ребро графа.
Именно решение данной задачи привело Л. Эйлера к доказательству приведённой выше теоремы. Кстати, согласно ей, данная задача неразрешима, поскольку степени всех вершин графа нечётны.
По сути дела, теорема приведенная ниже описывают условия, при которых можно построить геометрическую фигуру “не отрывая карандаша от бумаги”, одной сплошной линией. Только в первом случае начало и конец этой линии будут совпадать, а во втором случае они будут различны.
Эйлеровым путем в графе называется произвольный путь, проходящий через каждое ребро графа в точности один раз, т.е. путь v1, ..., vm+1, такой что каждое ребро e E появляется в последовательности v1, ..., vm+1 в точности один раз как e = {vi, vi+1 } для некоторого i.
Если v1 = vm+1, то такой путь называется эйлеровым циклом. Задача существования эйлерова пути в заданном графе была решена Эйлером в 1736 году, и представленное им необходимое и достаточное условие существования такого пути считается первой в истории теоремой теории графов.
Теорема. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем две вершины нечетной степени.
Доказательство.
Доказательство
достаточности условия теоремы будет
следствием анализа алгоритма нахождения
эйлерова пути, который будет описан
ниже. Необходимость условия очевидна,
так как если вершина v,
отличная от вершины v1
и vm+1,
появляется в эйлеровом пути k
раз, то это означает, что степень этой
вершины в графе составляет 2k.
Отсюда следует, что вершины нечетной
степени, если они существуют, являются
концами эйлерова пути. Здесь следует
отметить, что не существует графов с
одной только вершиной нечетной степени.
Действительно, обозначая степень вершины
v
через d(v),
имеем
ибо в указанной сумме каждое ребро {u,
v}
считается дважды: один раз в d(u)
и один раз в d(v).
Отсюда следует, что число вершин всегда
четно.
Если в связном графе нет вершин нечетной степени, то каждый эйлеров путь является циклом, так как концы эйлерова пути, не являющегося циклом, всегда вершины нечетной степени.
Предположим, что u и v — единственные вершины нечетной степени связного графа G = V, E, и образуем граф G* добавлением дополнительной вершины t и ребер {u, t} и {v, t} (или просто {u, v}, если {u, v} E ). Тогда G* — связный граф без вершин нечетной степени, а эйлеровы пути в G будут в очевидном взаимно однозначном соответствии с эйлеровыми циклами в G*. В силу этого дальше мы будем заниматься только эйлеровыми циклами.
Первые задачи теории графов были связаны с решением математических развлекательных задач и головоломок, например:
задача о кенигсбергских мостах (задача Эйлера), развитие которой привело к циклу задач об обходах графов;
задачи о перевозках, решение которых привело к созданию эффективных методов решения транспортных задач и др.