5. Парадокс Алле
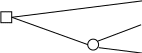
Виникає питання: чи не можна замінити ОПР автоматом і чи зберігаються при цьому які-небудь особливості людської поведінки? Для відповіді на це питання наведемо відомий парадокс Алле [3, с.43] (запропонований французьким вченим М.Алле), представлений двома лотереями на рис.7.
1
млн 0,1
А С 5
млн
5 млн 0,9 0
0,1
0,89 0,11
В 1 млн D 1 млн
0,01 0 0 0,89
Рис.7. Парадокс Алле
Позначимо: U(5 млн)=1; U(1 млн)=U; U(0)=0. У лівій лотереї є вибір між діями A (одержати 1 млн) і B (згодитись на лотерею). Переважна більшість людей віддає перевагу A. Із цього випливає U > 0,1 U+0,89 U або U > 10/11.
У правій лотереї є вибір між діями C і D (дві лотереї). Переважна більшість людей віддає перевагу варіанту C (майже та сама ймовірність програти, але виграш більше). Тоді 10,1 > 0,11U, тобто U < 10/11. Здійснюючи такий вибір, люди діють не відповідно до функції корисності.
6. Нераціональна поведінка. Евристики і зміщення
Значну частину фундаменту економіки як науки складає теорія корисності. І раптом у 70-і роки з’явились роботи, в яких систематично демонструвалось відхилення поведінки людей від раціональної. Авторами найбільш відомих робіт були психологи: А.Тверський, П.Словик, Б.Фішкоф, Д.Канеман та ін.
Наведемо один із найбільш відомих прикладів нераціональної поведінки людей – "дилему генерала" [3, с.45]. Генерал одержав поразку у війні і хоче вивести свої війська (600 чол.) з території супротивника. У нього є дві можливі дороги, і розвідка дала оцінки можливих втрат під час вибору кожної з них. Дані про дороги і можливі втрати представлені на рис.9.
200 чол. врятовані
Дорога1
Загін
600 чол. 600 чол. врятовані
p=1/3
Дорога 2
p=2/3 0 чол. врятовані
Рис.9. Дилема генерала
Більшість людей, які розглядали дилему, показану на рис.9, вибирають першу дорогу, намагаючись уникнути лотереї, коли в одному з випадків гине весь особистий склад з’єднання. Але ця ж дилема може бути представлена в іншому вигляді (рис.10). Тепер уже більшість людей вибирають другу дорогу, так як на ній з імовірністю p=1/3 можна врятувати все з’єднання. Легко побачити, що лотереї на рис.9 і 10 еквівалентні, але одна з них представлена у вигляді виграшів, а друга – у вигляді втрат.
400 чол. загине
Дорога1
Загін
600 чол. Ніхто не загине
p=1/3
Дорога 2
p=2/3 Усі 600 чол. загинуть
Рис. 10. Інше представлення дилеми генерала
Численні експерименти продемонстрували відхилення поведінки людей від раціональної, визначили евристики, які використовуються під час прийняття рішень. Наведемо перелік найбільш відомих евристик.
Судження за представництвом. Люди часто судять про ймовірність того, що об’єкт А належить до класу В тільки за схожістю А на типовий об’єкт класу В. Вони майже не враховують апріорні ймовірності, які впливають на цю належність. В одному з дослідів учасникам експерименту дали короткий опис суб’єктів із групи у складі 100 чол. і попросили визначити ймовірності того, що розглядуваний суб’єкт є інженером або юристом за умов: 1) у групі 70 інженерів і 30 юристів; 2) у групі 30 інженерів та 70 юристів. Відповіді були приблизно однакові. В інших експериментах було показано, що люди орієнтуються тільки на представництво, не враховуючи навіть розмір вибірки, за якою виноситься судження.
Судження за зустрічністю. Люди часто визначають імовірність подій із того, як часто вони самі стикались із цими подіями і наскільки важливими для них були ці зустрічі. Так, в одному з дослідів учасники експерименту оцінили ймовірність появи букви "k" в англійських словах на першому і третьому місці. Більшість людей легше згадує слова з буквою "k" на першому місці, і вони визначили відповідну ймовірність як більшу, хоча в дійсності справедливе обернене судження (на третьому місці буква "k" зустрічається значно частіше). Тверський і Канеман [3, с.46] відмічають, що багато людей, напевне, вірять у "закон малих чисел", який стверджує, що мала вибірка добре характеризує всю множину.
Судження за точкою відліку. Якщо під час визначення ймовірності використовується початкова інформація як точка відліку, то вона суттєво впливає на результат. Так, під час оцінки ймовірностей подій групам людей давали завищені й занижені початкові значення і просили їх скоректувати. Середні по групах оцінки істотно відрізнялись.
Зверхдовіра. В експериментах було показано, що люди занадто довіряють своїм судженням, особливо у випадках, коли вони говорять про минулі події. Люди переоцінювали свої судження про ймовірність рідкісних явищ природи, про ймовірність зміни курсу акцій на біржі і т.д. Вони настільки були впевнені у своїх судженнях, що ризикували певними сумами грошей.
Прагнення до виключення ризику. Численні роботи показують, що як в експериментах, так і в реальних ситуаціях люди прагнуть виключити ситуації, зв’язані з ризиком. Вони згоджуються на середні (і гірше середніх) альтернативи, тільки б не виникали ситуації, де хоча б при малих імовірностях були можливі великі втрати.