Лекция 6. Измерительные шкалы

Часто при моделировании сложных систем прибегают к разного рода экспериментам. Эксперименты бывают вычислительные и физические. Вычислительные осуществляются при помощи вычислительных машин.

Также эксперименты подразделяются на активные и пассивные. При пассивном эксперименте события фиксируются на входе и выходе системы, а при активном эксперименте мы воздействуем на некоторые входные параметры системы. Данные, которые появляются на входе и на выходе системы, могут быть измерены в различных измерительных шкалах.

Измерение – это алгоритмическая операция, которая данному наблюдаемому состоянию объекта, явления, процесса ставит в соответствие определенное значение: число, номер, символ.

Шкала наименований. Будем рассматривать только такие алгоритмы измерения, которые различимым объектам ставят в соответствие разные обозначения, а неразличимым объектам – одинаковые обозначения.

Такого рода измерения удовлетворяют следующим аксиомам:

1. А = В  B = A (эквивалентно);

2. А = В, В = С  А = С (эквивалентно тождественно);

3. А = В или А  В.

Измерения, удовлетворяющие данным аксиомам, называются измерениями в номинальной или классификационной шкале.

При обработке экспериментальных данных, измеренных в номинальной шкале, можно лишь проводить операции проверки их принадлежности определенным классам. Результаты сравнения представим при помощи символа Кронекера:

,

где δ_ij равен 1, если объект х_i принадлежит классу А_j и равен 0 в противном случае.

С результатами такого рода измерений можно выполнять более сложные преобразования, например, посчитать количество объектов, попавших в k-й класс:

.

Таким же образом можно вычислить относительную частоту:

,

где n – общее число измеряемых объектов.

Примеры измерений в номинальной шкале: имя, пол, место рождения, работы, учебы и т.д. человека; вид кредита, страховки, ценной бумаги; общественный строй государства, система правления и т.д.

Порядковые шкалы возникают в том случае, если при измерении в номинальной шкале появляется возможность в каком-то отношении сравнить разные классы.

Для измерений в порядковой шкале дополнительно к перечисленным аксиомам надо добавить аксиомы 4–5:

1. A B или B A (предпочтительнее);

2. A B, B C  A C.

Примеры: призовые места в конкурсе, воинские звнания, уровни качества продукции, экономический уровень развития города, региона, страны.

Существенной особенностью порядковых шкал служит то, что при установлении порядка никаким образом не определяется расстояние между сравниваемыми объектами. Поэтому результаты измерений в порядковой шкале, даже если они обозначены числами, нельзя считать обычными числами и производить с ними арифметические действия.

В порядковой шкале допустимы операции, позволяющие определить, какое из наблюдений х_i или х_j предпочтительнее.

Например, эту операцию можно осуществить с помощью следующей функции:

.

Для объектов, измеряемых в порядковой шкале, можно вычислить ранг R объекта по формуле .

Пример 1. В настоящее время рынок лекарственных препаратов широко представлен различными гипопротекторами. Чтобы сохранить нейтральность и невольно не сделать рекламу какому-либо препарату, выберем 10 наиболее популярных препаратов и обозначим их буквами А, В, С, D, E, F, S, G, H, J. Обратимся к ведущему специалисту-гастроэнтерологу с просьбой выразить свое предпочтение данным препаратам при помощи табл.2, в которой строки и столбцы соответствуют названиям препарата. Если препарат в названии строки предпочтительнее препарата в названии столбца, то в соответствующей ячейке на пересечении строки и столбца ставим 1, в противном случае 0. После недолгих раздумий эксперта-гастроэнтеролога таблица приобрела следующий вид:

Таблица 2.

Препарат	A	B	C	D	E	F	S	G	H	J	Ранг
A	–	1	0	1	1	1	0	1	1	1	7
B	0	–	1	1	1	1	1	1	1	1	8
C	1	0	–	0	1	0	1	1	1	0	5
D	0	0	1	–	0	0	0	0	1	0	2
E	0	0	0	1	–	1	1	1	1	1	6
F	0	0	1	1	0	–	0	0	1	1	4
S	1	0	0	1	0	1	–	0	1	1	5
G	0	0	0	1	0	1	1	–	1	1	5
H	0	0	0	0	0	0	0	0	–	1	1
J	0	0	1	1	0	0	0	0	0	–	2

Из табл. 2 следует, что наиболее предпочтителен препарат В, так как ему соответствует наибольший ранг, равный 8. Препарат А занимает 2-е место (ранг = 7), наименее предпочтительным оказался препарат H (ранг = 1), а препараты С, S, G имеют одинаковую степень предпочтения, поскольку ранг = 5. Ранги – обычные натуральные числа, с ними можно совершать арифметические операции, поэтому мнение одного эксперта – хорошо, а двух или больше – лучше, и мы можем повторить процедуру анализа предпочтений, но уже с другими экспертами. Так как ранги – это числа, то результаты проведенных опросов можно усреднить и получить более достоверную оценку предпочтительности гипопротекторов специалистами.

Традиционно в порядковых шкалах осуществляют измерение некоторых величин, непрерывных по своей природе. Такие шкалы называются модифицированными порядковыми шкалами. Примеры таких шкал: шкала твердости минералов, шкала силы ветра, силы землетрясения, шкала баллов учащихся, порядковая шкала Черчмена и Акоффа и др.

Шкала твёрдости минералов по Моосу. Введена в 1811 г. немецким минерологом Ф. Моосом, который предложил установить стандартную шкалу твердости, постулируя только 10 ее градаций. За эталоны приняты следующие минералы с возрастающей твердостью (твёрже считается тот минерал, который при соприкосновении с другим минералом оставляет на нем след): тальк, гипс, кальций, флюорит, апатит, ортоклаз, кварц, топаз, карунт, алмаз.

Шкала силы ветра по Бофорту введена в 1806 г. английским гидрографом и картографом адмиралом Ф. Бофортом, который предложил бальную шкалу силы ветра, определяя ее по характеру волнения моря: 0 баллов (безветрие) – штиль, умеренный ветер – 4 балла, сильный ветер – 6 баллов, шторм – 10 баллов, ураган – 12 баллов.

Шкала силы землетрясения введена в 1935 г. американским сейсмологом Ч. Рихтером, который предложил 12-балльную шкалу для оценивания силы землетрясения в зависимости от последствий прохождения их по данной территории.

Балльные шкалы учащихся также относятся к модифицированным порядковым шкалам. В российских школах принята 5-балльная, в вузах – 2-балльная (зачет, незачет) и 4-балльная система оценок. В некоторых европейских странах – 10-балльная система, а в англоязычных странах – 100-балльная. Шкала эта неточная, приблизительная. Преподаватели, пытаясь совершенствовать ее, вводят для себя дополнительные градации (плюс, минус, точки и т.д.). Эта шкала крайне необъективна. Отличники разных школ отличаются по уровню знаний. Это происходит потому, что эта шкала порядковая. В рамках класса она классифицирует учащихся по уровню знаний. И крайне неверно считать и учитывать среднеарифметический балл – величину, не имеющую смысла в порядковой шкале.

Порядковая шкала Черчмена и Акоффа. В социологических исследованиях часто оказывается полезным и возможным предложить опрашиваемому не только упорядочить заданный перечень альтернатив, но и указать хотя бы грубо силу предпочтения. Это позволяет при достаточно жестких требованиях к весовым коэффициентам перевести измерения в разряд более сильных шкал, нежели шкала порядка.

Пример. Пусть имеется 5 объектов. Сначала эксперта просят расположить их в порядке предпочтения: А В С D Е. Затем ему предлагают поставить в соответствие объектам любые числа между 0 и 1, выразив грубо степень предпочтения (табл. 3).

Таблица 3

A	B	С	D	Е
1	0,8	0,7	0,5	0,3

Далее необходимо уточнить с помощью вопросов действительный смысл предпочтений. Например, что он предпочитает А или В, С, Д, Е вместе взятые. Результат опроса необходимо выразить изменением весовых коэффициентов. Если А В, С, Д, Е вместе, то назначают новые значения коэффициентов так, чтобы коэффициент, соответствующий А был больше, чем сумма коэффициентов при В, С, Д, Е. Например (табл. 4):

Таблица 4

A	B	С	D	Е
1	0,4	0,3	0,15	0,05

Затем выясняется, предпочтительнее В или С, Д, Е вместе взятые и т.д. Цель – уточнение весовых коэффициентов.

Шкала интервалов появляется, если упорядочивание объектов можно выполнить настолько точно, что известны расстояния между двумя любыми объектами. Шкала интервалов единственна с точностью до линейных преобразований. Это означает, что равные интервалы измеряются одинаковыми по длине отрезками шкалы, где бы они на ней не располагались (рис.15).

Рис. 15

Если расстояния между объектами выражаются числами ∆х₁, ∆х₂, а в другой шкале при выборе других нуля и единицы – числами ∆у₁, ∆у₂, то для шкалы интервалов справедливо равенство

.

Из данного соотношения следует, что интервальные шкалы могут иметь произвольные начала отсчета и единицы измерения. Перейти от одной шкалы к другой можно с помощью линейного преобразования: y = ax+b, где а – единица измерения; b – начало отсчета.

Примерами величин, которые по своей физической природе либо не имеют абсолютного нуля, либо допускают свободу выбора в установлении начала отсчета и поэтому измеряются в интервальных шкалах, являются температура, время, высота местности. Начало летоисчисления у христиан установлено от рождества Христова, а у мусульман – на 622 г. позднее – от переезда Магомета в Медину. Высоту местности принято отсчитывать от уровня моря, и это привело к тому, что большая часть территории Голландии имеет отрицательную высоту. Работая со шкалой интервалов, надо помнить, что если мы проводим операции над измерениями по шкале, забыв об их относительности, то велик риск получить бессмысленные результаты. Например, если сказать, что температура воды увеличилась в 2 раза при ее нагреве от 9 до 18^°С, то для шкалы Фаренгейта это будет неверно, так как в этой шкале температура изменится от 37 до 42°С. В интервальной шкале доступна новая операция – определение расстояния между объектами. Над расстояниями можно выполнять любые арифметические операции.

Шкала отношений, в отличие от предыдущих, обладает тем свойством, что измерения в этой шкале – полноправные числа, т.е. с ними можно производить всевозможные арифметические операции. Для этой шкалы справедливо следующее свойство: отношение двух наблюдаемых значений измеряемой величины не зависит от того, в какой из этих шкал произведено измерение (рис. 16).

Так,

.

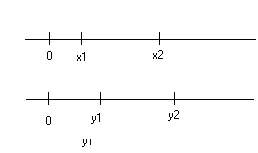Рис. 16

Этому условию удовлетворяет соотношение вида y = ax, т.е. для того чтобы перейти из одной шкалы в другую, необходимо выполнить преобразование y = ax. Это означает, что шкала отношений имеет естественный абсолютный 0, но остается свобода в выборе единиц (величина в шкале отношений не может быть показателем степени или основанием логарифма).

Абсолютная шкала имеет абсолютный 0, абсолютную единицу измерения. Эта шкала единственна и уникальна. Такими свойствами обладает абстрактная числовая прямая. Важная особенность этой шкалы – отвлеченность (безмерность) и абсолютность её единицы измерения. В природе она не существует. Указанные особенности позволяют произвести над показаниями абсолютной шкалы такие операции, которые недопустимы для показаний других шкал – применять эти показания в качестве показателя степени и аргумента логарифма.