Лекция 16. Некоторые аспекты практического применения эвм

Об особенностях практического применения вычислительной техники к математическому моделированию сложных систем можно говорить достаточно много. Рассмотрим некоторые наиболее важные аспекты.

Аспект 1. Вычислительная схема, реализованная на компьютере, иногда может отличаться от общепринятой аналитической схемы. Так, например, при аналитическом решении нелинейных дифференциальных уравнений второго порядка, если это возможно, то с помощью замены приводим к дифференциальному уравнению первого порядка. Предположим, надо решить дифференциальное уравнение

y^// = f(y, y^/), y = y(x).

Аналитическое решение предполагает замену y^/ = p(y), которая приведет к уравнению первого порядка pp^/ = f(y, p). Если нам удастся его решить, например, методом разделяющихся переменных, то будет найдено решение

p = φ(y, c₁),

которое представляет собой новое уравнение, но уже первого порядка:

.

Такая последовательность действий при аналитическом решении иногда приводит к цели. Однако при решении большинства практических задач интеграл в элементарных функциях не берется, поэтому приходится прибегать к численному интегрированию при помощи вычислительной техники. При решении задачи с помощью численных методов на вычислительной машине нецелесообразно понижать степень уравнения (неэкономично, в смысле объема произведенных вычислений), а следует сразу решать уравнение второго порядка численным методом.

Итак, надо уметь хотя бы грубо оценивать объем вычислительной работы, необходимой для доведения решения до конца. С развитием вычислительной техники вопросы формального интегрирования потеряли свое былое значение. Более того, изменился смысл выражения «задать функцию», поскольку функцию можно задать как хорошо алгоритмизируемое решение какой-либо задачи, и заданная таким образом функция ничем не хуже аналитически заданной функции.

Аспект 2. Возможности вычислительной техники большие, но не безграничные. Распространено заблуждение о том, что вычислительная машина справится с любым алгоритмом. Это далеко не так. Поэтому при решении сформулированной задачи на вычислительной машине обычно наиболее ответственным пунктом выступает подготовка задачи к программированию, т.е. выбор конкретной вычислительной схемы. Поясним сказанное на простом примере.

Пусть надо вычислить сумму бесконечного ряда

S = 1+1/2²+1/3²+…+1/n²+…

Полагаясь на компьютерные технологии, будем вычислять слагаемые и складывать члены ряда пока они не обратятся в машинный нуль, после чего частные суммы ряда перестанут возрастать. Оценим необходимое время для вычисления суммы ряда. Пусть машинный нуль равен 0,5·10^–25. Вычисления прекратятся, когда

1/n² < 0,5·10^–25, т.е. при .

Предположим, машина на вычисление очередного слагаемого и суммирование с ранее полученной суммой тратит t = 10^–6 с. Тогда нетрудно посчитать, что общее время вычислений составит

T= t·n = 4,5·10¹²·10^-6 = 4,5·10⁶ с, или (4,5·10⁶)/3600 = 1250 ч,

или 1250/24 = 52 дня.

Можно посчитать гораздо быстрее и точнее, если просуммировать, например, первые 10⁶ первых членов ряда (на это уйдет ≈ 1 с), а остаток заменить приближённой формулой остаточного члена ряда:

.

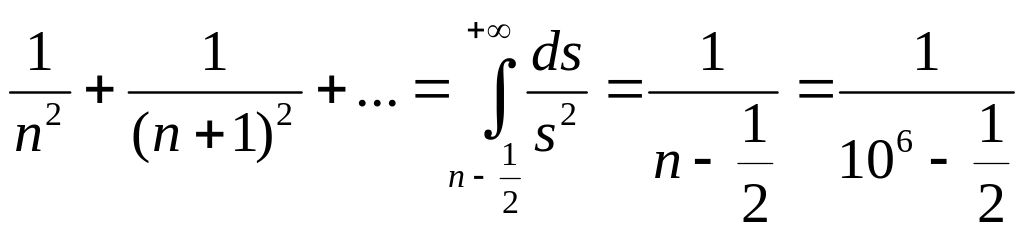В специальной литературе можно найти равенство , по которому с любой степенью точности можно вычислить сумму ряда.

Аспект 3. В применении вычислительных машин может возникнуть ряд важных специфических проблем. Машина обычно выдает обработанную информацию в виде последовательности дискретных чисел, поэтому, если решение не состоит из одного или нескольких таких чисел, возникает проблема придания решению такой формы, чтобы можно было его обозреть и им воспользоваться. При необдуманном задании вывода посчитанной компьютером информации может возникнуть ситуация, когда исследователь физически не в состоянии осмыслить, обработать эту информацию. Особенно эта проблема возникает при решении задач с параметрами.

Например, надо составить таблицу, по которой можно находить решение полного кубического уравнения

ax³ + bx² + cx + d = 0

при произвольных параметрах a, b, c, d. Предположим, каждый из параметров принимает по 50 значений, тогда число возможных комбинаций равно 50⁴ ≈ 6·10⁶ комбинаций. Вычислительной машине для вывода такого объема информации потребуется примерно ≈ 200 км бумаги и месяц непрерывной работы. Можно ли изменить ситуацию? Можно, для этого достаточно воспользоваться несложными преобразованиями. Сделаем замену:

, где .

Если обозначить , то получим уравнение, которое содержит всего один параметр:

z³ + rz + 1 = 0.

Таблицу значений решения последнего уравнения в зависимости от этого параметра уже нетрудно составить с помощью вычислительной машины, даже если ему придать не 50, а 500 значений.

Для неопытных пользователей компьютерной техники свойственно заблуждение, что нужно стремиться получить как можно больше информации. Проблема извлечения полезного вывода из моря цифр может оказаться более сложной, чем исходная задача. По этому поводу Хемминг заявил: «Прежде чем решать задачу, подумай, что делать с ее решением».

Аспект 4. При решении прикладных задач с использованием компьютерных технологий надо помнить, что неизбежны ошибки в результатах. Условно причины, порождающие ошибки, можно разделить на 4 категории:

1) ошибки, порождаемые выбором математической модели ( );

2) ошибки в исходных числовых данных ( );

3) погрешности вычислительного метода ( );

4) ошибки округления ( ).

Суммарная ошибка может быть найдена по формуле

.

В настоящее время, с все большей компьютеризацией решения задач, последняя причина приобрела особую актуальность. Когда в длинных цепочках вычислений последующие выкладки используют результаты предыдущих вычислений, ошибки округления могут разрастаться до такой степени, что с некоторого момента мы будем иметь дело в сущности лишь с одними ошибками. Рассмотрим пример такого эффекта.

Пример 1. Надо численно посчитать значение интеграла

,

Применяя интегрирование по частям (U = xⁿ, dV = e^xdx), нетрудно получить рекуррентное соотношение

I_n=1– n·I_n-1 , n = 0, 1, 2,… (*)

При n = 0 найдем значение I₀:

.

Далее найдем по рекуррентному соотношению и т. д. Результаты расчетов приведены в табл. 11.

Таблица 11

n	0	1	2	3	4	5	6	7	8	9
In	0,632	0,368	0,264	0,208	0,168	0,160	0,040	0,720	–4,76	37

Из табл.11 видно, что при n > 6 значения I_n явно нелепые, так как из выражения для I_n следует, что при росте n значения I_n должны убывать и стремиться к нулю. Причина ошибки в том, что погрешность при вычислении I₀ при каждой итерации умножается на n, т. е. фактически при n итерациях погрешность увеличивается фактически в n! раз. При n → ∞ значение интеграла стремится к 0, а погрешность при этом стремительно возрастает.

Исправить ситуацию можно, несколько изменив алгоритм таким образом, чтобы погрешности с каждым шагом не возрастали, а убывали. Заменим в соотношении (*) n на n+1 и перепишем его в виде

,

тогда

.

Эта формула дает возможность вычислять I_n, переходя от больших значений n к меньшим. За счет этого погрешность будет уменьшаться. Положим, некоторое отправное I_n = 0, например, пусть I₁₀ = 0, и запустим итерационный процесс. Результаты расчетов приведены в табл. 12. Более точные вычисления показывают, что I₉ = 0,092, а I₈ = 0,101.

Таблица 12

n	0	1	2	3	4	5	6	7	8	9	10
In	0,652	0,368	0,264	0,207	0,171	0,46	0,27	0,12	0,1	0,1	0

Ошибки округления при вычислении интегралов и дифференциальных уравнений могут создать парадоксальную ситуацию: с целью увеличения точности результата мы измельчаем шаги, но если применяемый метод выбран неудачно (неустойчив в вычислительном отношении), то из-за увеличения числа действий ошибки округления начинают сказываться сильнее и итоговая погрешность возрастает. Поэтому проверка вычислительной устойчивости применяемого метода и вообще влияние округления выступает существенной частью многих компьютерных вычислений. Для некоторых сравнительно простых классов задач удается провести строгое теоретическое исследование вычислительной устойчивости, которое позволяет понять, какие факторы и как влияют на эту устойчивость. Часто бывает удобнее, в том числе и для сложных задач, выяснить влияние ошибок округления эмпирически. Для этого выработан ряд мер. Например, можно произвести повторное вычисление с удвоенной точностью или с одной недостающей значащей цифрой во всех вычислениях и сравнить результаты с исходными. Если разница в результатах существенная, то, следовательно, округления значительно влияют на решение задачи.

Аспект 5. С проблемой влияния ошибок округления непосредственно связана проблема так называемой обусловленности системы уравнений, из которой определяются интересующие нас величины. Если система уравнений плохо обусловлена (det → 0), то малое изменение исходных данных (округление) может привести к значительному изменению в решении, даже если бы решение находилось с абсолютной точностью (аналитически). Рассмотрим пример плохо обусловленной системы.

Пример 2. Пусть имеем систему

.

Она имеет решение, полученное аналитически:

.

Однако, если правую часть во втором уравнении незначительно изменить, например, заменить на 2,00003, то решение станет совершенно иным:

.

В более сложных случаях плохая обусловленность может быть совсем неочевидной, тем более что она не вызывает препятствий для компьютерного решения задач. Как и вычислительная неустойчивость, она может быть обнаружена либо из теоретических соображений, либо эмпирически – путем повторного вычисления с измененными в рамках реально осмысленной точности исходными данными.

Аналогичные трудности возникают при решении «некорректных задач», для которых как угодно малое изменение исходных данных может привести к существенному изменению или даже к исчезновению решения. Для успешного решения таких задач на вычислительной технике и дальнейшего практического применения результата необходимо вовремя выявить эти особенности и применить специально разработанные методы, например, регуляризацию.