Лекция 11. Интерполяция и экстраполяция при моделировании сложных систем

Идеи и методы теории интерполяции сравнительно хорошо формализованы, однако есть некоторый произвол в выборе интерполирующей функции и критерия качества интерполяции. При этом учитываются объем исходных данных, их точность и достоверность, цель интерполяции и т.д. Самые грубые задачи интерполяции возникают при подборе эмпирических формул и в других сходных ситуациях.

Чаще всего пользуются формулами простой структуры, например:

y = ax+b, y = ax²+bx+c, y = ax³+bx²+cx+d, y = и т.п.,

учитывая при ее выборе те или иные теоретические соображения, связанные, например, с поведением функции при х → ∞ или х → 0 и т.п. После выбора интерполирующей функции и метода интерполяции (например, метода наименьших квадратов) можно найти параметры a, b, c, d, т.е. построить функцию. Альтернативным служит графический метод выровненных точек.

Увеличивая число параметров в формуле, можно добиться того, что интерполирующая функция будет всё точнее описывать процессы, происходящие в системе. Более того, указанным условиям с помощью интерполяционного многочлена Лагранжа n – 1 степени можно удовлетворить совершенно точно. Но из этого совсем не следует, что с увеличением степени полинома Р_n(x) качество его как интерполирующей функции всё время возрастает, вплоть до насыщения при n = k – 1.

Дело в том, что при достаточно больших n интерполяционный многочлен Р_n(x) слишком жёстко определяется исходными данными и поэтому повторяет все случайные отклонения, обусловленные ошибками экспериментов, шумовым фоном процесса. Кроме того, с ростом n существенно растут сложность вычислений и их вычислительные погрешности.

Рассмотрим простой пример, иллюстрирующий, что при построении интерполяционного многочлена второй степени могут получиться более некорректные результаты, чем с интерполяционным многочленом первой степени (рис. 20).

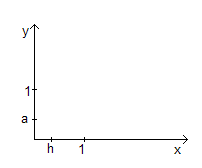
Рис. 20

Пусть требуется произвести интерполяцию по заданным значениям y(0) = 0, y(h) = a, y(1) = 1, 0< h < 1. Интерполяционный полином будем искать в виде многочлена второй степени y = ax²+bx+c. Поскольку число неизвестных равно числу уравнений, то квадратичная функция пройдет через заданные точки, а неизвестные параметры a, b, c найдем, решив простейшую систему трех уравнений с тремя неизвестными:

Получим

c = 0, = , = .

Запишем полученный полином в нестандартном, но удобном для нас виде:

.

Предположим, что при вычислении а получена некоторая погрешность δа. Тогда соответствующая погрешность для интерполяционного полинома будет равна

.

Пусть . Тогда .

Из этой формулы видно, что при или погрешность интерполяционного полинома стремится к ∞, т.е. при h, близких к 0 или 1, ошибки интерполяции могут быть весьма значительными. Опасные участки значений h выделены красным цветом. Таким образом, интерполяционный многочлен второй степени дает плохую аппроксимацию при h, близких к 0 и 1.

Рассмотрим, как себя ведет при этих значениях h полином первой степени y = ax + b. Параметры a, b найдем по методу наименьших квадратов:

,

где y_i – заданные значения функции; y_i^*– значения, вычисленные по полиному первой степени:

y = bx+ c.

Чтобы найти значения параметров полинома b, c, надо выписать и решить систему нормальных уравнений, которая получается дифференцированием суммы квадратов отклонений = y_i – y_i^* по b и c. Система нормальных уравнений для многочлена первой степени имеет вид

С учетом значений n, х, у система примет вид

Решив систему относительно b и c, найдем их значения:

, .

Запишем полученный интерполяционный многочлен первой степени в виде, удобном для дальнейшего исследования:

.

Тогда, если а измерено с погрешностью , получим ошибку интерполяционного многочлена

.

Пусть , тогда

.

По этой формуле, если , то , и если , то . К тому же значение квадратного трехчлена h² – h + 1 в вершине принимает значение 3/4, поэтому h² – h + 1 » 3/4, т.е. не близко к 0, поэтому погрешность полинома

не принимает бесконечно большое значение, следовательно, погрешность устойчива относительно малых ошибок в определении а.

Таким образом, полином первой степени лучше интерполирует на концах отрезка [0; 1], чем полином второй степени.

Данный пример показал, что не всегда целесообразно использование интерполяционных многочленов высокой степени. Оптимальную степень таких многочленов для различных классов задач можно получить, проводя дополнительные исследования.

Необходимо иметь в виду, что интерполирующая функция дает лишь некоторое модельное описание истинной зависимости, которое может иметь как высокую, так и не очень высокую степень достоверности. В частности, при интерполировании «в слепую» без глубокого анализа реального смысла зависимостей всегда имеется опасность не заметить разрывы, острые экстремумы и другие особенности, которые могут оказаться для этой зависимости определяющими.

Во многих математических моделях систем удобно использовать в качестве интерполирующих функции, заданные не одной формулой, а двумя или несколькими, действующими на различных интервалах изменения независимой переменной. Это относится как к зависимостям, определенным на достаточно длинных интервалах и неописываемым с приемлемой точностью единой формулой, так и к зависимостям, обладающим разрывами. В первом случае широко применяются кусочно-полиномиальные функции, в том числе

так называемые сплайны, значительно лучше приспособленные для интерполирования, чем функции, заданные единой формулой.

Если при интерполяции обсуждение реального смысла исследуемой зависимости полезно, то при экстраполяции такое обсуждение во всех случаях является центральным, решающим элементом процедуры. Как указывалось ранее, интерполяция одной и той же зависимости может быть осуществлена различными формулами. Однако, если даже эти формулы на интервале интерполирования дают близкие значения, то при удалении от этого интервала они могут приводить к принципиально различным результатам.