Лекция 13. Многокритериальность в моделировании сложных систем

Часто этап содержательной постановки задачи системного анализа приводит нас к выводу о наличии нескольких целей функционирования системы. В самом деле, если некоторая экономическая система может иметь главную цель – достижение максимальной прибыли, то почти всегда можно наблюдать наличие ограничений или условий. Нарушение этих условий либо невозможно (тогда не будет самой системы), либо заведомо приводит к недопустимым последствиям для внешней cреды. Итак, ситуация, когда цель всего одна и достичь ее требуется любой ценой, практически маловероятна.

Пусть x – некоторая альтернатива из множества X. Считается, что для любого x X можно задать некоторую функцию q(x), которую называют критерием и которая обладает тем свойством, что если альтернатива x₁ предпочтительнее альтернативы x₂ (x₁ x₂), то q(x₁) > q(x₂). Предполагается, что q(x) – числовая функция.

Если считать, что выбор любой альтернативы приводит к однозначно известным последствиям (т. е. выбор в условиях определённости), то наилучшей альтернативой x* является та, которой соответствует наибольшее значение критерия (т. е. x* – это аргумент, максимизирующий q(x)):

Данная задача на вид проста, но зачастую сложен метод её решения, так как он зависит от характера множества X, от размерности x (в общем случае x – это вектор), от вида функции q(x). На практике редко встречаются задачи, в которых альтернатива x оценивается одним числом. Решение задачи выбора при нескольких критериях (q(x) – это вектор-функция), качественно отличающихся друг от друга, является ещё более сложной задачей, чем рассмотренная задача.

Таким образом, для оценивания альтернатив используется несколько критериев q_i(x), I = 1...p. Может быть такой случай, когда на множестве X найдётся альтернатива, для которой все критерии имеют наибольшее значение. Эта альтернатива и будет оптимальным решением задачи выбора. Но на практике такие случаи бывают крайне редко.

Рассмотрим (обзорно) несколько наиболее типичных способов решения многокритериальных задач оптимизации.

1. Сведение к однокритериальной. Вводится суперкритерий, который представляет собой скалярную функцию от критериев q_i(x), i = 1 ...p. Суперкритерий бывает аддитивной или мультипликативной функцией:

где – веса, отражают относительный вклад частных критериев в суперкритерий, s_i – коэффициент, позволяющий перейти к безразмерным величинам от q_i (для мультипликативной функции ещё и условие ).

Задача сводится к максимизации или минимизации суперкритерия, т.е.

Данный способ имеет ряд существенных недостатков:

– такую функцию сложно максимизировать;

– не формализована процедура выбора весовых коэффициентов;

– получаемое оптимальное решение очень чувствительно к изменению весов.

Пример 1. Пусть задано множество X, . Найдём направление возрастания критерия q_s по линиям уровня или по градиенту. Пусть оно соответствует grad . Тогда из рис. 21 следует, что оптимальное решение – x*. Допустим, незначительно изменили весовые коэффициенты: . При этом значительно изменится направление возрастания функции, предположим, оно соответствует grad . Как видно из графика, получим совсем другое решение x**.

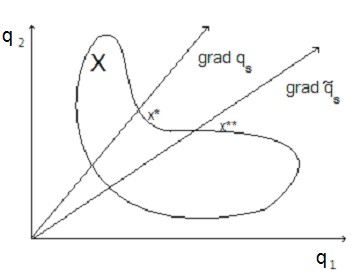
Рис. 21

2. Условная максимизация. Выделяется основной критерий и рассматриваются остальные как дополнительные. При этом задача формулируется как задача нахождения условного экстремума основного критерия. Пусть q₁ – основной критерий. Остальные зафиксируем на определённом уровне q_i(x) = c_i, i = 2…p.

.

Пример 2. Для возможности графической иллюстрации также ограничимся рассмотрением случая с двумя критериями q₁(x), q₂(x), считая q₁ основным критерием. Зафиксируем значение критерия q₂ на определенном уровне, например, q₂ = с₂. Тогда задача оптимизации будет иметь вид

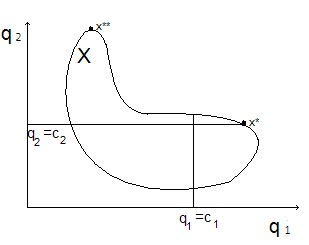
Рис. 22

Из рис. 22 видно, что оптимальным решением будет точка x*, которая соответствует наибольшему значению q₁ вдоль прямой с = q₂.

В некоторых задачах целесообразно задавать ограничения на дополнительные критерии не в виде уравнений, а в виде неравенств q_i(x) ≤ c_i.

Пусть теперь q₂ – основной критерий, а q₁(x )≤ c₁:

Как видно из графика, оптимальным решением будет точка x**, которая соответствует наибольшему значению q₂ в области q₁(x )≤ c₁.

3. Поиск альтернативы с заданными свойствами. Предположим, что заранее можно указать значение частных критериев q_i(x), i =1…p, соответствующих наилучшей альтернативе x*:

Задача состоит в том, чтобы найти альтернативу, удовлетворяющую этим требованиям, либо установить, что такая альтернатива отсутствует, и потом найти в X такую альтернативу, которая больше всего похожа на оптимальную. Величины называются уровнем притязаний, а точки их пересечения в n-мерном пространстве критериев – целью. Как уже было замечено, x* может находиться как внутри области допустимых решений, так и вне области. В первом случае эту точку надо найти, что является чисто технической задачей. Во втором случае задача оптимизации состоит в том, что, начав с любой альтернативы, надо приблизиться к x* по некоторой траектории в пространстве Х. Задача решается введением числовой меры близости между очередной альтернативой х и целью x*, т.е. между векторами q(x) = (q₁(x), …, q_p(x)) и . Можно, например, в качестве меры близости использовать метрику

.

Пример 3. На рис. 23 оптимальное решение x* находится вне области допустимых решений. Тогда решением может быть какая-либо из точек x₁*, x₂* или некая другая, в зависимости от выбранной метрики. Очевидно, что решением будет точка, лежащая на границе области.

Рис. 23

4. Нахождение паретовского множества. Множество Парето – это множество несравнимых альтернатив. Предполагают, что предпочтение одной из двух альтернатив можно отдавать только в том случае, если она по всем критериям лучше другой. Если же предпочтения хотя бы по одному критерию расходятся с предпочтениями по другим, то такие альтернативы признаются несравнимыми. Осуществляя попарно сравнение, все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся, несравнимые между собой принимаются. Если все максимально достижимые значения частных критериев не относятся к одной и той же альтернативе, то принятые альтернативы образуют множество Парето и выбор на этом заканчивается. При необходимости выбора единственной альтернативы следует привлекать дополнительные инструменты: вводить новые, добавочные критерии и ограничения, бросить жребий либо прибегнуть к услугам экспертов.

Пример 4. Для возможности графической иллюстрации также ограничимся рассмотрением случая с двумя критериями q₁(x), q₂(x). Множество допустимых решений (альтернатив) расположено внутри изображенной на рис.25 области. Очевидно, что для любой альтернативы внутри области можно указать другую более предпочтительную альтернативу (на рис. 24 правее и выше исходной альтернативы). Поэтому множество наиболее предпочтительных альтернатив расположено на правой границе области между выделенными точками. Альтернативы данного множества образуют множество Парето, так как они несравнимы друг с другом. Каждая из них «лучше» по одной альтернативе, но «хуже» по другой.

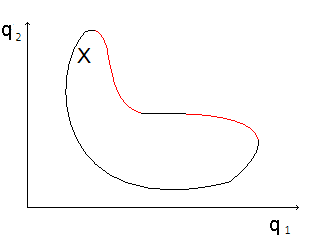
Рис. 24