
- •Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
- •Основы гидравлики
- •Содержание
- •1. Рабочая программа 7
- •2. Гидростатика 10
- •3. Основы кинематики и динамики жидкости 34
- •4. Гидравлические сопротивления 51
- •5. Гидравлический расчет трубопроводов 65
- •Введение
- •1.Рабочая программа
- •Введение
- •2.Гидростатика
- •2.1.Основные физические свойства жидкости и газа.
- •2.2.Вязкость жидкости.
- •2.3.Силы, действующие в жидкости
- •2.4.Абсолютное Гидростатическое давление и его свойства
- •2.5.Дифференциальные уравнения равновесия жидкости
- •2.6.Поверхность равного давления и ее свойства
- •2.7.Основное уравнение гидростатики
- •2.8.Приборы для измерения абсолютного, манометрического давлений и давления вакуума
- •2.9.Сила давления жидкости на наклонную плоскую стенку
- •2.10.Точка приложения силы давления жидкости на плоские стенки.
- •2.11.Сила давления жидкости на криволинейные поверхности
- •2.12.Примеры и задачи
- •3.Основы кинематики и динамики жидкости
- •3.1.Основные понятия и определения гидродинамики
- •3.2.Уравнение неразрывности потока
- •3.3.Уравнение Бернулли для струйки идеальной жидкости
- •3.4.Уравнение Бернулли для струйки и потока реальной жидкости
- •3.5.Интерпритации уравнения Бернулли
- •3.6.Примеры и задачи
- •4.Гидравлические сопротивления
- •4.1.Виды гидравлических сопротивлений
- •4.2.Ламинарное и турбулентное движение жидкости
- •4.3.Основное уравнение равномерного движения
- •4.4.Ламинарный режим движения
- •4.5.Турбулентный режим движения
- •4.6.Экспериментальные исследования коэффициента гидравлического сопротивления
- •4.7.Примеры и задачи
- •5.Гидравлический расчет трубопроводов
- •5.1.Расчет Коротких трубопроводов
- •5.1.1.Уравнение простого трубопровода
- •5.1.2.Первый тип расчета
- •5.1.3.Второй тип расчета
- •5.1.4.Третий тип расчета
- •5.2.Расчет газопроводов при малых перепадах давлений
- •5.3.Примеры и задачи
- •5.4.Расчет газопроводов при Больших перепадах давлений
- •5.5.Гидравлический удар в трубах
- •5.6.Примеры и задачи
- •6.Гидравлический расчет истечения жидкостей
- •6.1.Истечение жидкости из малого отверстия в тонкой стенке
- •6.2.Истечение жидкости через внешний илиндрический насадок.
- •8.2.Гидравлические элементы живого сечения потока в канале.
- •8.3.Основные расчетные формулы для открытых русел
- •8.4.Основные задачи при расчете трапецеидальных каналов на равномерное движение воды.
- •8.5.Расчет безнапорных труб
- •8.6.Примеры и задачи
- •9.Литература
2.7.Основное уравнение гидростатики
Рассмотрим несжимаемую жидкость = const(p), находящуюся в поле силы тяжести. В поле силы тяжести ускорения массовых сил равны X = 0, Y = 0, Z = - g. Тогда дифференциальное уравнение равновесия жидкости запишется
dp = - g dz. |
(2.0) |
Интегрируя последнее уравнение при условии, что в точке z = z0, давление равно p = p0 получим
p = p0 + g (z0 - z). |
(2.0) |
Выберем точку с индексом ‘0’ на поверхности жидкости рис. 2.4. Обозначим разность координат точек z0 - z = h – глубина погружения данной точки (где ищется давление) под свободной поверхностью жидкости. Тогда основное уравнение гидростатики запишется
p = p0 + g h. |
(2.0) |
2.8.Приборы для измерения абсолютного, манометрического давлений и давления вакуума
Р |
pат = p0 + рт g hрт = рт g hрт, |
(2.0) |
И тогда высота столба ртути равна
|
(2.0) |
Атмосферное давление также измеряется механическими барометрами.
Манометрическим давлением pм называется разность абсолютного и атмосферного давления, или избыток абсолютного давления над атмосферным давлением.
pм = p - pат. |
(2.0) |
Манометрическое давление может меняться в пределах – pат < pм < ∞.
Давлением вакуума pv называется разность абсолютного и атмосферного давления, или недостаток абсолютного давления над атмосферным.
pv = pат - p. |
(2.0) |
Давление вакуума может меняться в пределах –∞ < pv < pат.
2.9.Сила давления жидкости на наклонную плоскую стенку
Представим на рис. 2.4, а открытый сосуд, наполненный жидкостью и имеющий плоскую наклонную стенку ОМ. В плоскости этой стенки наметим оси координат Оу и Ох. Ось Ох направим перпендикулярно к плоскости чертежа.
-
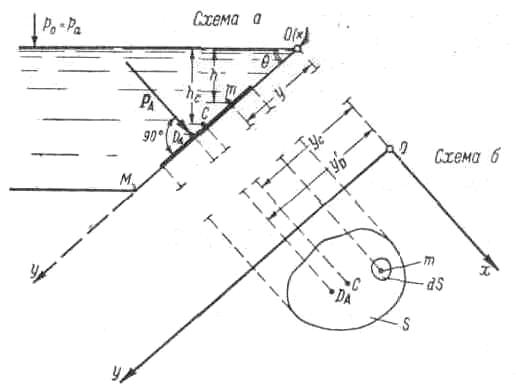
Рис. 2.6 -Давление жидкости на плоскую наклонную фигуру площадью S
На стенке сосуда ОМ наметим некоторую плоскую фигуру любого очертания, имеющую площадь S. Эта фигура на рис. 2.4, будет проектироваться в линию (показанную на чертеже жирно). Представим еще на рис. 2-15, б стенку сосуда ОМ, повернутую относительно оси Оу на 90° (совмещенную с плоскостью чертежа). Ясно, что на рис. 2.4 намеченная плоская фигура будет изображаться без искажения.
В соответствии с первым свойством гидростатического давления можем утверждать, что во всех точках площади S давление жидкости будет направлено нормально к стенке. Отсюда заключаем, что сила абсолютного гидростатического давления pa, действующая на произвольную плоскую фигуру площадью S, будет также направлена по отношению к стенке нормально (как это показано на рис. 2.4).
Поставим перед собой цель найти:
а) величину силы PA абсолютного гидростатического давления;
б) положение линии действия силы PA
Наметим
на рассматриваемой фигуре произвольную
точку т, заглубленную под
уровнем жидкости на величину
![]() и имеющую координату
и имеющую координату
![]() ,
ясно, что
,
ясно, что
|
(2.0) |
где
![]() - угол
наклона боковой стенки сосуда к горизонту.
- угол
наклона боковой стенки сосуда к горизонту.
У
точки т выделим элементарную
площадку
![]()
![]() .
Сила абсолютного гидростатического
давления, действующая на эту площадку,
.
Сила абсолютного гидростатического
давления, действующая на эту площадку,
|
(2.0) |
или согласно (2-40)
|
(2.0) |
Интегрируя
это выражение по всей площади
![]() ,
получаем:
,
получаем:
|
(2.0) |
Ясно, что:
|
(2.0) |
где
![]() - статический
момент плоской фигуры относительно оси
Ох;
- статический
момент плоской фигуры относительно оси
Ох;
уС- координата центра тяжести (точки С) данной плоской фигуры.
Подставляя (2-79) в (2-78), получаем:
|
(2.0) |
Так
как
![]()
где
![]() -
заглубление центра тяжести
-
заглубление центра тяжести
![]() плоской фигуры под горизонтом жидкости,
то
плоской фигуры под горизонтом жидкости,
то
|
(2.0) |
Или
|
(2.0) |
где
![]() -абсолютное гидростатическое давление
в точке, являющейся центром тяжести
рассматриваемой плоской фигуры.
-абсолютное гидростатическое давление
в точке, являющейся центром тяжести
рассматриваемой плоской фигуры.
Формулу (2.37) можно представить еще в виде:
|
(2.0) |
здесь![]() - сила,
обусловленная атмосферным (поверхностным)
давлением, передающимся через жидкость
на плоскую фигуру:
- сила,
обусловленная атмосферным (поверхностным)
давлением, передающимся через жидкость
на плоскую фигуру:
|
(2.0) |
![]() - сила
избыточного (весового) давления:
- сила
избыточного (весового) давления:
|
(2.0) |
где![]() - избыточное
(весовое) давление в центре тяжести
фигуры.
- избыточное
(весовое) давление в центре тяжести
фигуры.
Как видно, сила гидростатического давления (абсолютного или избыточного), действующая на плоскую фигуру любой формы, равна площади этой фигуры, умноженной на соответствующее гидростатическое давление ( или ) в центре тяжести этой фигуры.
Точка
![]() пересечения
линии действия силы
пересечения
линии действия силы
![]() с
плоскостью, в которой лежит рассматриваемая
фигура, называется центром давления
силы
.
Найдем положение точки
с
плоскостью, в которой лежит рассматриваемая
фигура, называется центром давления
силы
.
Найдем положение точки
![]() ,
этим и определится линия действия
силы
.
,
этим и определится линия действия
силы
.

 ис.
2.5
ис.
2.5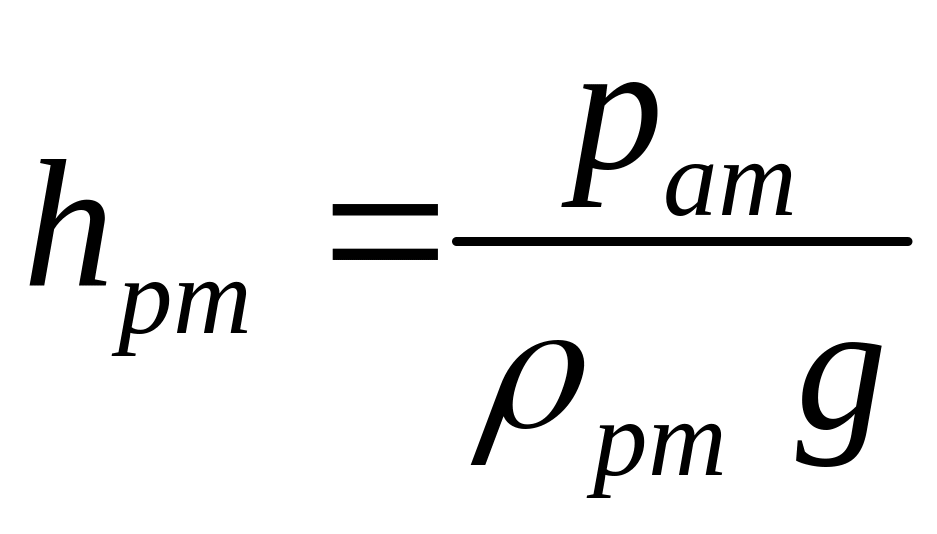 .
.