8.3.5 Анализ модели.

После вычисления коэффициентов модели необходимо оценить ее пригодность. Как и в случае корреляционно-регрессионного анализа, такая проверка называется проверкой адекватности модели.

8.3.5.1. Проверка значимости коэффициентов модели.

Проверка значимости каждого коэффициента проводится независимо с помощью критерия Стьюдента. Она включает следующие операции:

1. Расчет дисперсий опыта.

2. Оценку однородности дисперсий опытов.

3. Расчет дисперсии параметра оптимизации.

4. Вычисление дисперсии коэффициентов регрессии.

5. Проверку значимости коэффициентов регрессии по критерию Стьюдента.

Расчет дисперсии опытов и оценка их однородности

Так как каждый опыт несет в себе какую-то ошибку, для ее уменьшения производят повторение опытов при тех же условиях, т.е. в каждой строке таблицы планирования. Построчные дисперсии подсчитываются по формуле.

; (8.7)

где r - число повторных опытов.

После вычисления дисперсий их однородность оценивается с помощью критерия Кохрана:

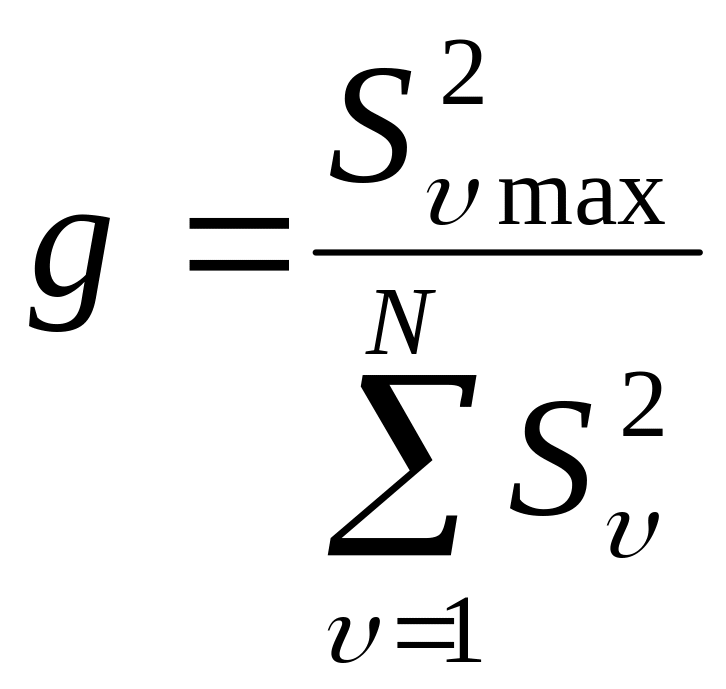. (8.8)

Вычисленное значение g сравнивается с табличным. Гипотеза об однородности дисперсий принимается в том случае, если экспериментальное значение g не превышает табличного.

Расчет дисперсий параметра оптимизации и коэффициентов регрессии

Если дисперсии параллельных опытов однородны, то вычисляется дисперсия параметра оптимизации S²_у (дисперсия воспроизводимости ):

. (8.9)

Если параллельные опыты отсутствуют, то S²_y можно рассчитать по формуле

Определение дисперсии коэффициентов регрессии производится по формуле (8.10)

где N - число точек плана; r - число параллельных опытов.

Проверка значимости коэффициентов регрессии

Для проверки значимости коэффициентов рассчитываются значения t_i -критерия:

(8.11)

По таблицам выбирается критическое значение t_кp, определяемое в зависимости от числа степеней свободы k=N(r-1) и заданного уровня доверительной вероятности β. Если t_i > t_кp, то коэффициент b_i признается значимым. В противном случае b считается статистически незначимым,

т.е. b_i = 0.

Пример 8.3. По данным табл. 8.5 оценить значимость коэффициентов уравнения, рассчитанных в примере 8.2.

Последовательно определим дисперсии опытов в каждой точке плана по формуле (8.7):

S²₁ = [(22-24) +(24-24) +(26-24) ]/2=4;

S²₂ = [(20-20) +(16-20) +(24-20) ]/2=16;

S²₃ = [(16-22) +(24-22) +(26-22) ]/2=28;

S²₄ = [(21-25) +(25-25) +(29-25) ]/2=16;

S²₅ = [(53-55) +(55-55) +(57-55) ]/2=7;

S²₆ = [(48-50) +(49-50) +(53-50) ]/2=9;

S²₇ = [(52-55) +(57-55) +(56-55) ]/2=7;

S²₈ = [(53-55) +(54-55) +(58-55) ]/2=7;

Определим значение критерия Кохрана g по формуле (8.8).

g = 28/(4+16+28+16+4+9+7+7)=0,308.

При уровне значимости =0,05, числе степеней свободы числителя f=r-1=2 и знаменателя m=N=8 g_табл= 0.52. Следовательно, дисперсии опытов однородны, так как g < g_табл

Рассчитаем дисперсии параметра оптимизация и коэффициентов регрессии, использовав для этого формулы (8.9) и (8.10) соответственно:

S²_y =11.375; S²_bi=0,47.

Применяя формулу (8.11), определяем значения t -критерия:

|t₁|=1,6; |t₂|=2,13;|t₃|=32,98; |t₁₂| =1.06; |t₁₃| =1,06; |t₂₃| =0.53; |t₁₂₃| =1,06.

'По таблице выбираем значение t_кр в зависимости от числа степеней свободы k=8(3-1)=16 и уровня доверительной вероятности β=0.95: t_кр=2,12. Сравним полученные значения t₁ с t_кр.

t₁<2.12; t₂>2.12; t₃>2.12; t₁₂>2.12; t₁₃<2.12; t₂₃<2.12; t₁₂₃<2. Следовательно, значимыми можно признать коэффициенты b₂=1, b₃=32,98, b₁₂=3.2. Остальные коэффициенты уравнения регрессии, выведенные в примере (8.2), можно не учитывать. Тогда рассматриваемое уравнение значительно упростится:

y =38,25-x₂+15.5x₃+1.5x₁x₂