5.7. Проверка гипотезы равенства двух выборочных

дисперсий.

Пусть имеются две выборки из нормальной совокупности. Объем каждой выборки равен n₁ и n₂. Дисперсии этих выборок соответственно равны S и S . Можно ли считать при наличии некоторых различий между величинами S и S , что данные выборки принадлежат одной и той же генеральной совокупности. Или можно вопрос поставить так: произведено два опыта, из которых один опыт производился с фактором A, а другой - без него. Каждый опыт повторялся n раз. В результате обработки статистических данных получено, что дисперсия признака X в опытах с фактором A равна величине S , а без него S . Оказывает ли влияние исследуемый фактор A на признак X?

Для ответа на поставленные вопросы необходимо произвести сравнение дисперсий и оценить, является ли существенным их различие. Сравнение дисперсий производится по их отношению:

F = S / S .

В числителе всегда ставится наибольшее значение из двух наблюденных дисперсий. Для проверки гипотезы необходимо вычислить значение F, определить r_{1 =} n₁ – 1 и r₂ = n₂ – 1 , где n₁ и n₂ - обьемы выборок и найти для r₁ и r₂ табличное значение F_Т. Если F F_Т , то расхождение не случайно, если F F_Т, то гипотеза принимается.

Пример. С двух автоматов, обрабатывающих одинаковые детали, взяты две выборки n₁ = n₂ = 1. При этом оказалось, что S = 400 мкм², S = 325 мкм². Ранее установлено, что рассеивание размеров подчинено нормальному закону.

F = 400/325 =1,23.

По таблицам выберем F_T в зависимости от уровня значимости = 0,05 и r₁ = r² =9: F_T = 3,23. Следовательно, гипотезу о несущественном расхождении S и S можно считать верной.

Примечание. Если выборки берутся из совокупности, незначительно отличающейся от нормальной, то для сравнения дисперсий можно пользоваться критерием F. Если совокупность имеет распределение, значительно отличающееся от нормального, то можно сравнить дисперсии только для больших выборок. В этом случае за критерий оценки можно взять отношение:

Е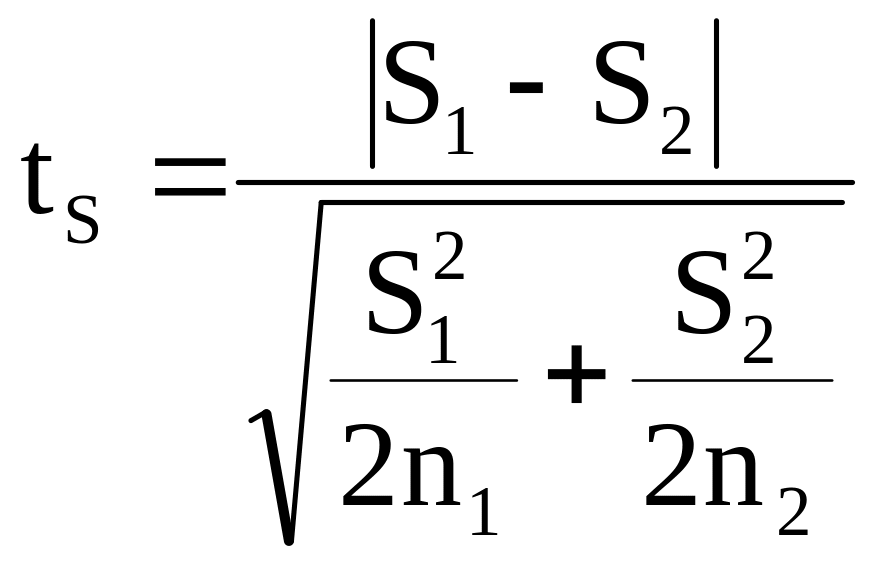 сли t_S 3 , то расхождение существенно, если t_S 3 - не существенно.

5.8. Проверка гипотезы равенства ряда дисперсий .

Пусть имеется m выборок неравных объемов n_i, взятых из одной или m генеральных совокупностей, имеющих нормальные распределения. Вычислены дисперсии выборок S , S , ... , S . Требуется проверить гипотезу о том, что различие дисперсий выборок носит случайный характер, т.е. все выборки принадлежат одной генеральной совокупности. Сравнение дисперсий проводится с помощью критерия Бартлета или критерия Кохрана .

Критерий Бартлета.

При использовании критерия Бартлета определяется вначале средневзвешенная дисперсия :

S² = S (n – 1)/(N – m) , где N = n_i.

Бартлет доказал, что случайная величина

Q = - 1/C (n_i – 1)ln S /S²,

где C = 1 + 1/3(m – 1)( 1/(n_i -1) – 1/(N – m)

имеет распределение близкое к распределению ² при заданном уровне значимости . Это значит, что гипотеза о равенстве дисперсий принимается, если Q . Величина C всегда больше 1. При использовании критерия Бартлета вначале вычисляется величина

B = – (n_i – 1)ln S /S²

и сравнивается с ². Если B < ², то гипотеза о равенстве принимается, если нет, то вычисляется C, затем Q и Q сравнивается с ².

Пример. С четырех блоков автоматических роторных линий взяты выборки по 100 шт. Требуется определить, обеспечивают ли блоки одинаковую точность по разностенности деталей после первой вытяжки. В результате статистической обработки данных получены следующие значения дисперсий:

S = 0,001418 мм²; S = 0,0013 мм²; S = 0,001098 мм²;

S = 0,0012 мм².

Определим средневзвешенную дисперсию:

S² = S (n – 1)/(N – m) = S /4:

S² = (0,001418 + 0,0013 + 0,001098 + 0,0012) = 0,001254;

B = 2,303 [ 4 lg0,001254 – 99 (lg0,001418+lg0,0013+lg0,001098 + +lg0,0012)=1,54

Выбираем уровень значимости = 0,05 , ² = 7,81.

Так как B < ², следовательно, Q будет и подавно меньше ², поэтому C вычислять не следует.

Таким образом все 4 блока обеспечивают одинаковую точность по разностенности.

В тех случаях, когда объемы выборок равные, лучше пользоваться не критерием Бартлета, а критерием Кохрана.