1.13. Переходный процесс в индуктивно связанных катушках

Пусть даны две индуктивно связанные катушки (рис.1.13.1.), причем вторичная обмотка замкнута накоротко, и полученная цепь подключается к источнику постоянного напряжения.

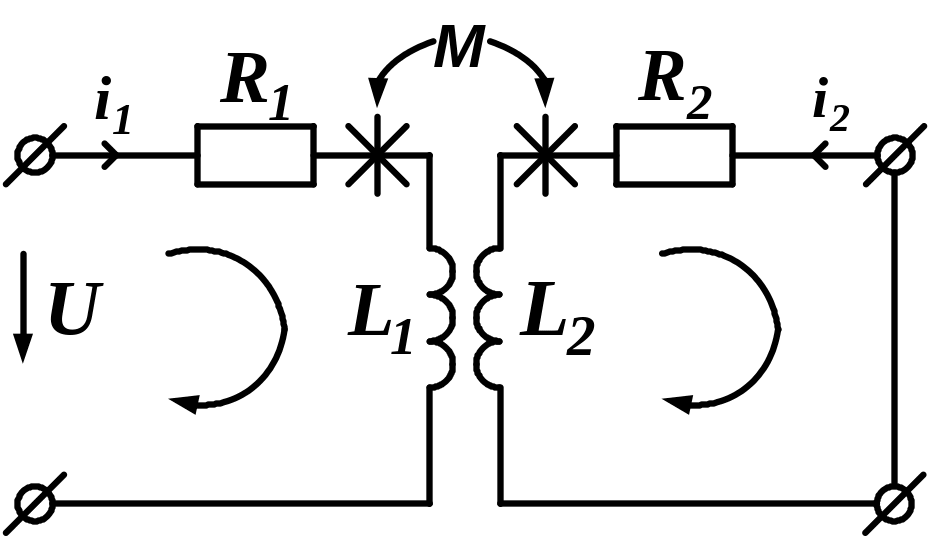
Рис.1.13.1. Индуктивно связанные катушки

Будем полагать, что катушки включены согласно, причем R₁ = R₂ = R, L₁ = L₂ = L. Данная схема представляет собой линейный трансформатор в режиме короткого замыкания. Составим уравнения электрического равновесия для первичной и вторичной обмоток трансформатора. Определим токи i₁ и i₂ в переходном процессе:

. (1.13.1)

Для решения полученной системы воспользуемся операторным методом. Считая, что начальные условия нулевые, перепишем систему уравнений в операторной форме:

, (1.13.2)

где

и .

Совместным решением уравнений трансформатора и перехода к оригиналам токов с помощью формулы разложения получаем оригиналы функций i₁ и i₂:

; (1.13.3)

.

Из анализа полученных уравнений следует, что при М = 0 (отсутствует индуктивная связь) или i₂ = 0 уравнения упрощаются:

;

i₂(t) = 0.

Выражение для тока i₁ соответствует подключению цепи R-L к источнику постоянного напряжения, которое получено раньше. Построим для наглядности зависимость тока i₁(t) как при наличии, так и при отсутствии индуктивной связи:

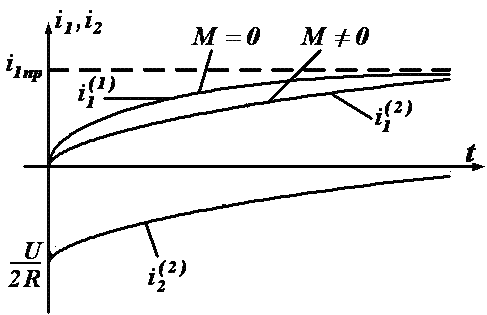
Рис.1.13.2. Токи первичной и вторичной обмоток трансформатора

в переходном процессе

Причина такого изменения тока i₁ при М ≠ 0 состоит в том, что i₂ препятствует изменению тока i₁, увеличивая тем самым постоянную времени в первой катушке. Для построения i₂ сделаем преобразования.

.

Наличие взаимной индуктивности увеличивает время переходного процесса.

1.14. Интеграл Дюамеля

Интеграл Дюамеля позволяет проводить расчет переходного процесса при воздействии на линейную цепь напряжения (тока) произвольной формы.

Этот метод расчета основан на принципе наложения.

При этом входное воздействие сложной формы представляется в виде суммы слагаемых более простой формы, для которых легко найти реакцию цепи. Интеграл Дюамеля, который и есть сумма этих реакций, позволяет найти реакцию цепи на сложное воздействие.

Пусть на вход некоторого пассивного двухполюсника подано напряжение произвольной формы (рис 1.14.1.):

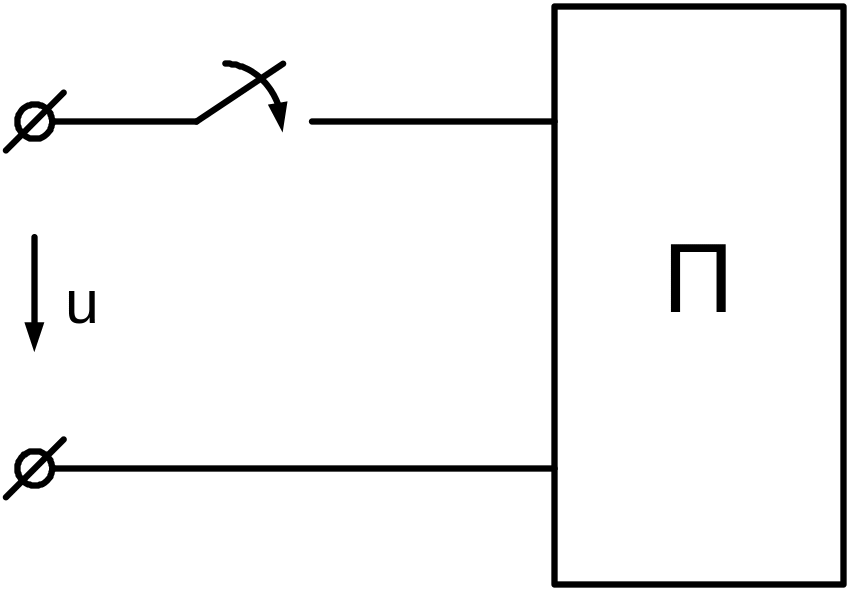
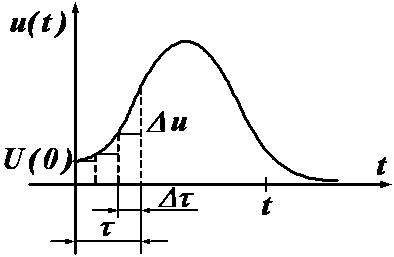
Рис.1.14.1. Пассивный двухполюсник и поданный на него сигнал

Выберем некоторый произвольный момент наблюдения t и рассчитаем переходный процесс к этому времени. Хотя он выбран произвольно, считаем его фиксированной величиной. Для обозначения текущего времени введем переменную τ, поэтому u(t) или i(t) – функции момента наблюдения, а u(τ) или i(τ) -функции текущего времени τ.

Первоначально заменим заданную на рис.1.13 функцию ступенчатой, приближенно заменяющей заданную кривую.

Из замененной ступенчатой кривой следует, что в момент времени t=0 напряжение на входе двухполюсника скачком изменилось от нуля до , а в любой промежуток времени τ возникает новый скачек напряжения , который существует, начиная с момента времени τ до бесконечности. Очередной скачек напряжения смещен во времени относительно предыдущего на .

Таким образом, приближенно входное напряжение можно представить в виде

. (1.14.1)

При определении реакции цепи, например, тока i(t) необходимо рассматривать его как сумму реакций на воздействие начального скачка напряжения и всех последующих скачков напряжения . Полагая известной переходную характеристику h(t), ток приближенно можно представить в виде

. (1.14.2)

Для получения точного решения для тока, соответствующего заданному закону изменения напряжения источника, необходимо уменьшить до бесконечно малой величины , а число скачков напряжения n увеличить до бесконечности . При этом заменяем на . В итоге величину скачка можно представить в виде

.

Сумма в пределе перейдет в интеграл и тогда точное выражение для тока i(t) в любой фиксированный момент времени будет иметь вид

. (1.14.3)

Полученное выражение называется интегралом Дюамеля.

Данная форма записи интеграла Дюамеля соответствует непрерывной функции подводимого напряжения. Однако в ряде случаев форма этого напряжения может быть представлена кусочно-непрерывной функцией, имеющей разрывы непрерывности первого рода. Интеграл Дюамеля применим и в этом случае.

Пусть на вход пассивного двухполюсника подано напряжение, представленное на рис.1.14.2

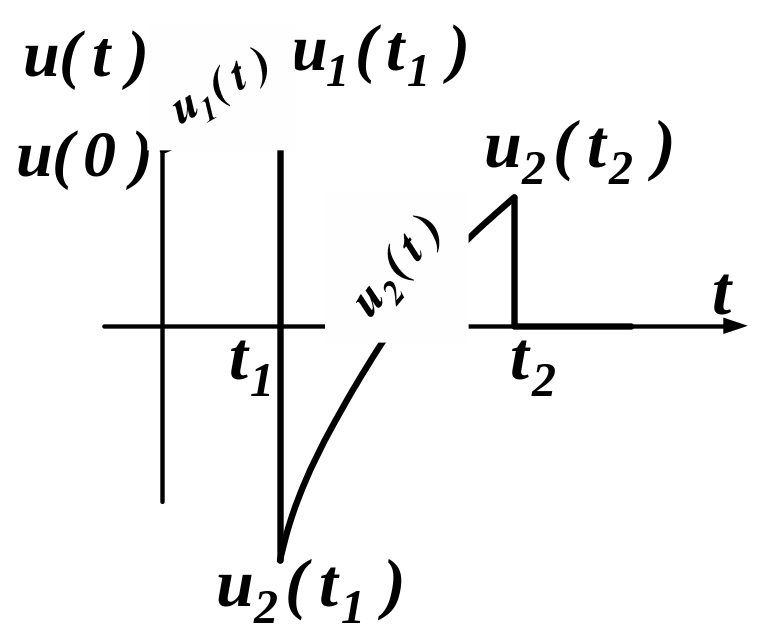
Рис.1.14.2 График входного напряжения с разрывами непрерывности

первого рода

Этот график можно разбить на 3 отдельных интервала, в пределах которых входное напряжение изменяется монотонно. Это интервалы: ; ; . В точках, соответствующих моментам времени , , происходят скачки непрерывности функции напряжения. В каждом из этих интервалов решение для определенного тока или напряжения имеет вид, отличный от решения на других интервалах.

Будем полагать, что переходная характеристика h(t) для определения тока известна.

Найдем решение для i(t) на всей оси t:

1. ;

.

Верхний предел интеграла открыт, поскольку в результате решения мы должны получить функцию тока, т.е. иметь возможность определить i в любой момент времени [0; t₁].

2. t₁ ≤ t < t_2;

.

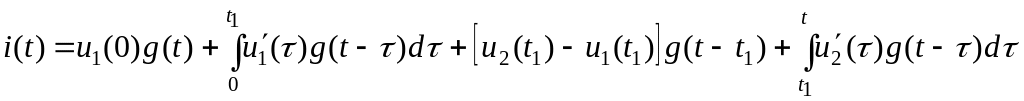3. t ≥ t_2;

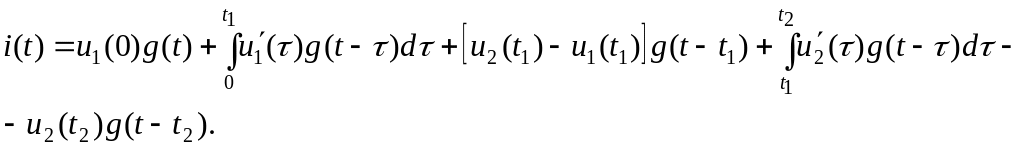
Проверка осуществляется на участках сопряжения:

в момент коммутации при t = 0 (только для первого решения) и при .