1.7. Операторный метод расчета переходных процессов

Наряду с классическим методом расчета переходных процессов, операторный нашел весьма широкое практическое применение, обусловленное известными преимуществами. Основная сложность расчета классическим методом состоит в определении постоянных интегрирования.

По мере возрастания сложности электрических цепей и порядка дифференциальных уравнений решение задачи существенно усложняется.

В основу операторного исчисления положено прямое преобразование Лапласа

, (1.7.1)

где f(t)- функция времени, называемая оригиналом,

F(p)- функция комплексной переменной , называемая изображением функции f(t).

Cвязь оригинала и изображения может быть представлена следующими символами:

; .

С помощью преобразования Лапласа операции дифференцирования и интегрирования заменяются операциями умножения и деления изображения функции F(p) на p, и вместо системы дифференциальных уравнений получают систему алгебраических уравнений относительно изображений функций.

Таким образом, преобразование Лапласа дает возможность вместо системы дифференциальных уравнений относительно оригинала функций решить систему алгебраических уравнений относительно изображений функций.

При этом необходимо от изображения искомой функции F(p) перейти к оригиналу f(t).

Функция f(t) должна удовлетворять следующим условиям:

1) функция f(t) со своими производными непрерывна на всей оси t;

2) функция f(t) возрастает не быстрее показательной функции: существуют постоянные числа и , такие, что для всех t

Функция f(t) может возрастать во времени, но темп ее роста не может превысить темпа убывания экспоненты. Для всех функций, которые мы рассматриваем в теории цепей, изображения искомых функций могут быть найдены.

Запишем изображение ряда функций, наиболее часто встречаемых при расчете переходных процессов:

;

;

,

где а - любое комплексное число, в том числе и мнимое:

.

Изображение производной и интеграла:

Запишем изображения функций: и .

Пусть , тогда

(1.7.2)

Чтобы учесть заряд конденсатора при t < 0, запишем напряжение на конденсаторе следующим образом:

.

Первое слагаемое определяет напряжение на конденсаторе к моменту возникновения переходного процесса в цепи.

Следовательно

.

Тогда изображение напряжения на конденсаторе имеет вид

. (1.7.3)

1.8. Закон Ома в операторной форме

Пусть дана некоторая цепь, из состава которой выделена ветвь, рис.1.8.1.

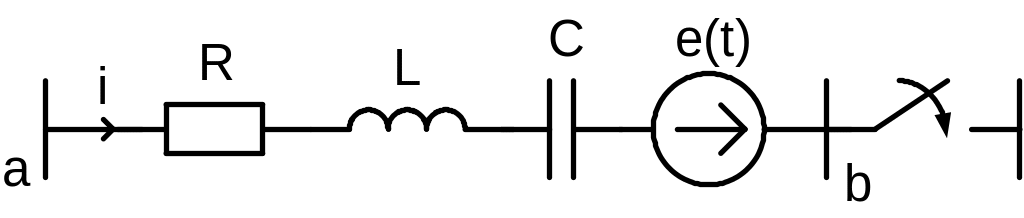
Рис.1.8.1. Произвольная ветвь электрической цепи

На основании обобщенного закона Ома для участка цепи:

.

Пусть направление тока совпадает с Э.Д.С.

Уравнение ветви для оригиналов функций:

.

Уравнение ветви для изображений функций:

;

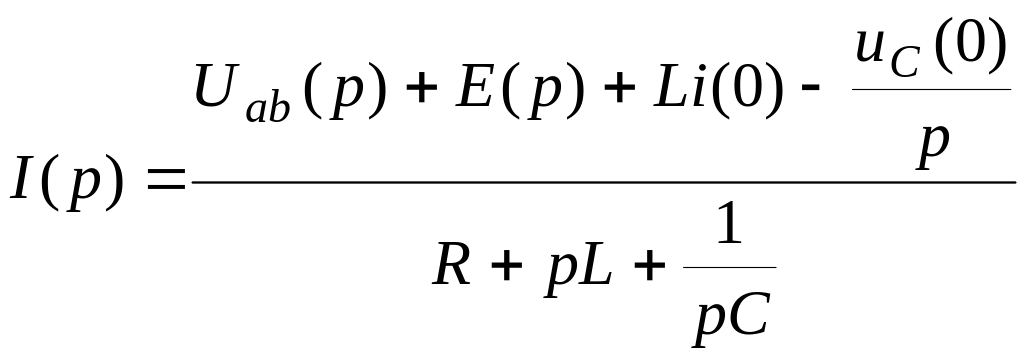. (1.8.1)

Полученное выражение представляет собой закон Ома в операторной форме:

повторяет полностью комплексное сопротивление данной ветви в установившемся режиме при протекании синусоидального тока, если заменить p на jω, и носит название операторного сопротивления цепи. В составе числителя полученного уравнения появилось два новых слагаемых: Li(0) и - это так называемые внутренние или операторные источники энергии, которые с физической точки зрения характеризуют энергию, запасенную в электрическом и магнитном полях к моменту коммутации. При нулевых начальных условиях эти слагаемые будут отсутствовать и уравнения при этом упростятся. Полученное выражение позволяет составить так называемую послекоммутационную операторную схему ветви и цепи (рис. 1.8). При этом в операторной схеме отсутствуют какие-либо переключатели.

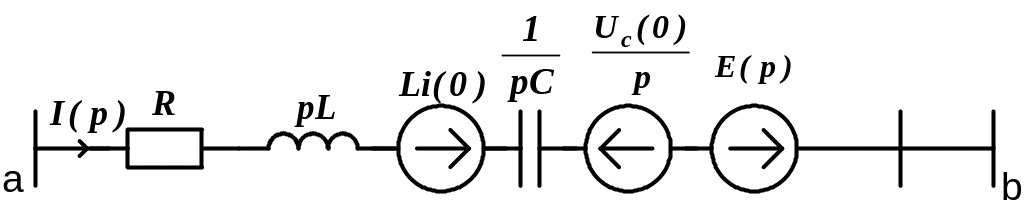
Рис.1.8.2.Операторное изображение ветви ,представленной на рис.1.8.1.