Определение коэффициентов нормальной системы уравнений

1	0,1	1,25	0,01	0,001	0,0001	0,125	0,0125
2	0,2	1,38	0,04	0,008	0,0016	0,276	0,0552
3	0,3	1,56	0,09	0,027	0,0081	0,468	0,1404
4	0,4	1,78	0,16	0,064	0,0256	0,712	0,2848
5	0,5	1,95	0,25	0,125	0,0625	0,975	0,4875
6	0,6	2,31	0,36	0,216	0,1296	1,386	0,8316
7	0,7	2,52	0,49	0,343	0,2401	1,764	1,2348
8	0,8	2,81	0,64	0,512	0,4096	2,248	1,7984
9	0,9	3,14	0,81	0,729	0,6561	2,826	2,5434
10	1,0	3,52	1,00	1,000	1,0000	3,520	3,5200
11	1,1	4,12	1,21	1,331	1,4641	4,532	4,9852
12	1,2	5,01	1,44	1,728	2,0736	6,012	7,2144
	7,8	31,35	6,50	6,084	6,071	24,844	23,1082

Нормальная система имеет вид

Решив систему методом Гаусса (см. лабораторную работу №1), получим

следовательно, функция имеет вид

Найдем невязку

3. Построим график функции и экспериментальные точки:

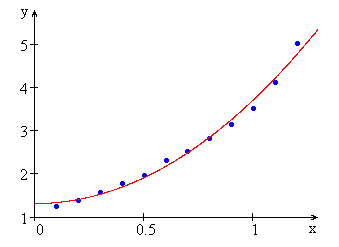
Рис. 5.5. График полученной параболы и экспериментальные точки

4. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab5.mcd. Вводим таблицу значений:

5. Вычисляем коэффициенты аппроксимации многочленами третьего и четвертого порядков. Для этого поочередно вводим в программу и .

Для первого случая компьютер выведет вектор коэффициентов функции :

и выписываем аппроксимирующий многочлен третьего порядка и его невязку

Для второго случая компьютер выведет вектор коэффициентов

и выписываем аппроксимирующий многочлен четвертого порядка и его невязку

6. Далее проводим аппроксимацию эксперимента линейной комбинацией четырех функций . В файле Lab5.mcd запрограммировано нахождение коэффициентов этой комбинаций, как с помощью решения нормальной системы уравнений, так и с использованием стандартной функции системы Mathcad linfit (см. п. 6.2). Для этого вводится векторнозначная функция

.

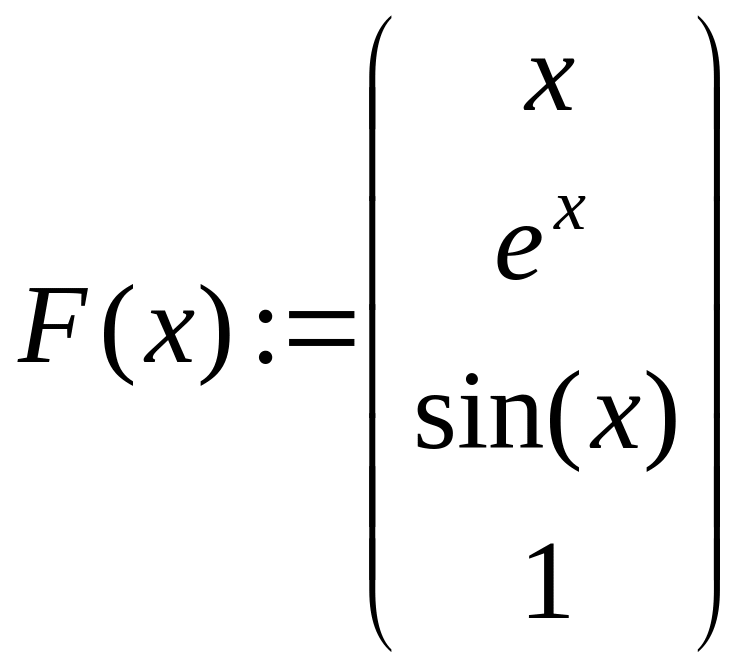Автоматически получаем вектор коэффициентов комбинации

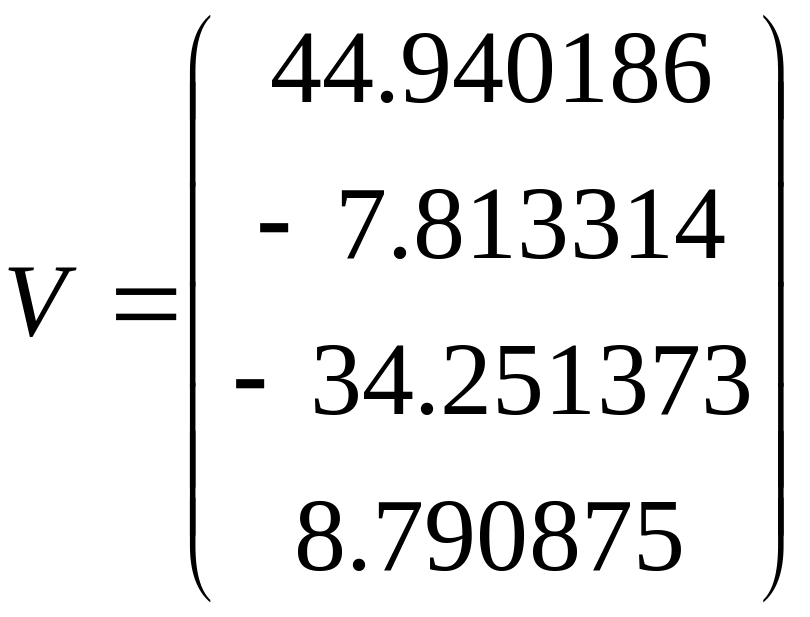
и невязку

.

Следовательно, аппроксимирующий закон имеет вид

.

7. Аналогично предыдущему пункту проведем аппроксимацию эксперимента, используя для примера восемь систем трех функций:

Перемножая скалярно соответствующие векторнозначные функции F на вектора коэффициентов разложения V, найденные в программе, выписываем все восемь законов с указанием соответствующих невязок :

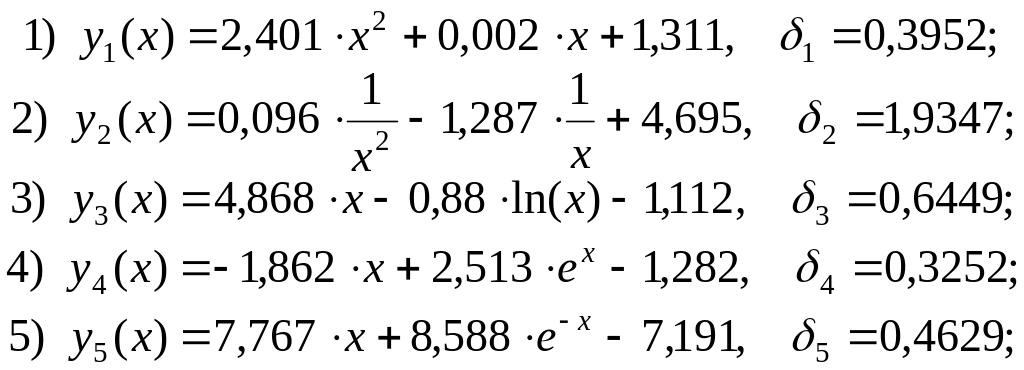
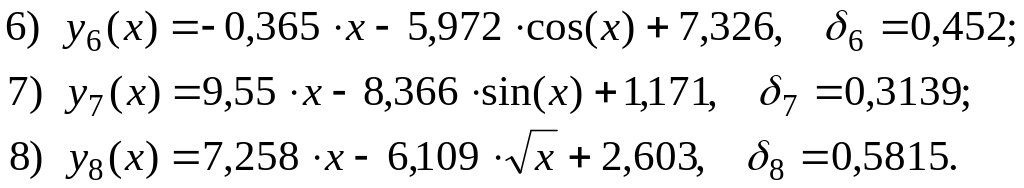
Анализируя величины невязок, делаем вывод, что наиболее приемлемыми законами являются 7, 4 и 1-й.

На компьютере строим графики этих функций (вместо , и примера строим свои лучшие законы).

8. В конце файла приведен пример применения метода Лагранжа, апроксимации экспериментальных данных многочленом 11-го порядка. Невязка данной аппроксимации будет равна нулю, так как через любые n точек с абсциссами можно точно провести многочлен ( )-го порядка.

9. Все расчеты оформляются в виде отчета по лабораторной работе.