Б 26. Уравнение Ильковича; диффузионный ток и его зависимость от концентрации деполяризатора.

Вывод выражения для градиента концентрации у растущего капельного электрода более сложен. Илькович исходил из предположения, что диффузия к капельному электроду происходит так же, как и к плоскому электроду. Если принять во внимание рост капли, то первоначальное дифференциальное уравнение диффузии изменится, так как на градиент концентрации влияет относительная скорость движения поверхности капли (вызываемая ее расширением) навстречу потоку диффузии и уменьшение вследствие этого толщины диффузионного слоя. Вывод дифференциального уравнения для линейной диффузии к растущему капельному электроду можно осуществить, исходя из следующих представлений.

Представим частицу деполяризатора в непосредственной близости от поверхности электрода. Вследствие роста капли ртути из чисто геометрических соображений (без учета диффузии) следует, что частица будет приближаться к поверхности электрода. Это движение по направлению к поверхности капли (конвекция), происходящее со скоростью v = dx/dt, обусловливает изменение концентрации со временем на некотором постоянном расстоянии от поверхности капли. Это изменение концентрации зависит от градиента концентрации и скорости движения среды (конвекции):

. (4.43)

Следовательно, общее изменение концентрации деполяризатора со временем равно

, (4.44)

где (дс/∂t)_дифф. означает изменение концентрации со временем, обусловленное диффузией, для которого справедлив второй закон Фика.

После подстановки в уравнение (4.44) значений из выражений (4.39) и (4.43) получим

. (4.45)

где v — вектор скорости.

Движение электродной поверхности эквивалентно движению раствора к воображаемой неподвижной поверхности. Уравнения (10) учитывает линейную диффузию и конвекцию к поверхности растущей капли. Скорость движения поверхности капли навстречу диффузионного потока можно связать с площадью S растущей капли

. (4.46)

Площадь S меняется во времени согласно уравнению

. (4.47)

Подставляя (4.47) в уравнение (4.46) находим

. (4.48)

Используя последнее выражение на основании уравнения (4.45), получаем окончательное выражение второго закона Фика для диффузии к растущему капельному электроду

. (4.49)

Это уравнение описывает перенос вещества к растущему электроду. Для его решения Илькович принял начальные и граничные условия, аналогичные условиям для решения уравнения (4.39). Решив это уравнение, Илькович получил выражение для градиента концентрации у поверхности растущего капельного электрода

. (4.50)

При сравнении этого уравнения с выражением для градиента концентрации при ли­нейной диффузии к стационарному электроду видно, что они различаются лишь числовым коэффициентом в знаменателе, который показывает, как под влиянием роста капли происходит уменьшение толщины диффузионного слоя.

Если выражение для (dc/dt)_x=0 подставить в уравнение (4.38), то для мгновенного тока, определяемого диффузией к растущему ртутному капельному электроду, получим

. (4.51)

Подставляя в уравнение (4.51) выражение для поверхности капельного электрода S = 0,85m^2/3t^2/3 и объединяя все числовые константы, находим окончательное уравнение Ильковича для мгновенного тока

. (4.52)

Если концентрации с и с₀ выражены в моль/см^-3 диффузионный коэффи­циент — в см²·сек ^-1, т (скорость вытекания ртути) — в г·сек ^-1 и t (время от начала роста капли) — в сек, то ток I будет выражаться в амперах.

Уравнение Ильковича в таком виде определяет значение тока во всех точках обратимой полярографической кривой, т. е. при любой величине потенциала ртутного капельного электрода, обусловливающей с₀. При увеличении отрицательного значения потенциала происходит уменьшение концентрации деполяризатора у электрода, и при достаточно отрицательных потенциалах с₀=0. Значение мгновенного тока, которое не зависит от дальнейшего увеличения катодного потенциала, равно, таким образом,

. (4.53)

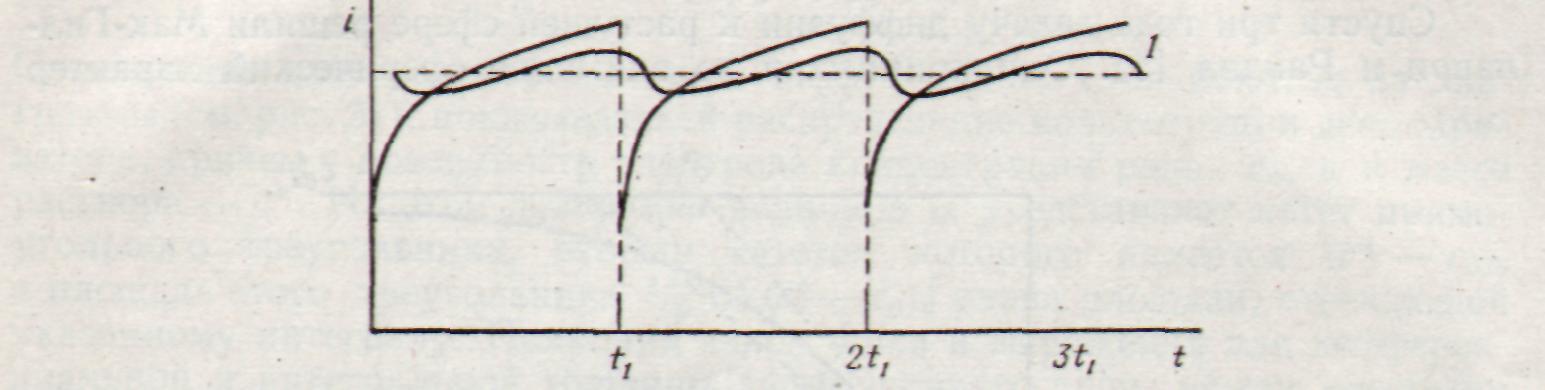
На каждой растущей капле сила тока со временем растет по закону I = kt^1/6 от нуля до максимальной величины непосредственно перед отрывом капли, и такое изменение тока повторяется на каждой капле (рис. 4.5). Площадь, ограниченная каждой отдельной кривой зависимости силы тока от времени (кривые I—t ), дает количество электричества в кулонах (если I выражено в амперах, а t – в секундах). Кривые типа, показанного на рис. 30, можно получить, если регистрировать зависимость силы тока от времени при постоянном потенциале с помощью с помощью осциллографа.

Однако при обычных полярографических измерениях обычно пользуются приборами для измерения тока, которые регистрируют только небольшие осцилляции около среднего значения тока .

Рис. 4.5. Схематическое изображение зависимости мгновенного и среднего диффузионного токов от времени.

Для среднего тока за период жизни капли t_max можно написать

, (4.54)

поэтому

. (4.55)

Из сравнения мгновенного тока перед отрывом капли I_max и среднего тока следует, что

(4.56)

Это означает, что гальванометр регистрирует осцилляции около среднего значения силы тока, которое равно 6/7 мгновенного максимального тока, т. е. силы тока перед отрывом капли. При с₀ = 0 для так называемого сред­него предельного диффузионного тока, который не изменяется с потенциа­лом, получаем выражение

. (4.57)

В полярографической литературе этот средний предельный диффу­зионный ток обычно называется просто диффузионным током, а выражение (4.51) — уравнением Ильковича. Уравнения для мгновенного тока или для токов, меньших предельного, являются лишь другими видами этого уравнения.

В американской и русской литературе широко приме­няется написание уравнения Ильковича для мгновенного тока в виде

, (4.58)

а для среднего тока

. (4.59)

В этих выражениях число Фарадея входит в числовую константу, скорость вытекания ртути т выражена в миллиграммах в 1 сек, а концентрация — в миллимолях на 1 л; сила тока при этом выражается в микроамперах.

В отличие от токов на стационарных электродах значения диффузион­ного тока, получаемые при работе с ртутным капельным электродом, хорошо воспроизводятся.

Из уравнения Ильковича следует, что при данных значениях т и t_max, т. е. при работе с одним и тем же капилляром при постоянной высоте столба ртути, диффузионный ток пропорционален аналитической концентрации деполяризатора в растворе:

, (4.60)

где — константа Ильковича,

. (4.61)

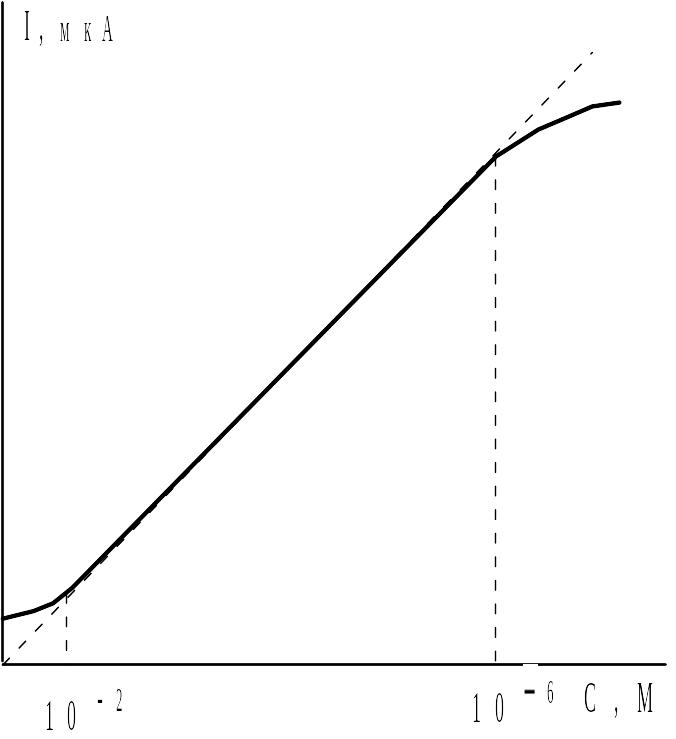
Уравнение Ильковича является основой количественного полярографического анализа. Если нанести на график значения диффузионного тока (или высоты волны, например, в миллиметрах) в зависимости от концентрации деполя­ризатора (рис. 4.6), то получается прямая, проходящая через начало коор­динат, которую можно использовать в качестве калибровочного гра­фика для определения неизвестной концентрации того же вещества. Например, диффузионный ток ионов кадмия пропорционален концентра­ции Cd²⁺ в области от 1,9·10^-5 до 1,2·10^-2 М, т. е. при более чем 600-кратном изменении концентра­ции иона кадмия. Отклонения от линейной зависимости при концентрациях деполяризатора меньше 10^-5 М объясняются тем, что в этих условиях диффузионный ток становится меньше тока заряжения электрода (емкостного тока), который не зависит от концентрации деполяризатора. При концентрациях деполяризатора с > 10^-2 М невозможно полностью исключить влияние миграционного тока.

Рис. 4.6. Зависимость диффузионного тока от концентрации деполяризатора	Рис. 4.7. Зависимость диффузионного тока от корня квадратного из высоты ртутного столба

Природу тока, протекающего через РКЭ, легко определить, изучив зависимость величины тока от высоты ртутного столба. Если при постоянной концентрации вещества изменять высоту столба ртути, то одновременно изменяются скорость вытекания ртути т и период капания t_max. Скорость истечения ртути т прямо пропорциональна, a время жизни капли t_max обратно пропорционально высоте столба ртути h:

; .

Подстановка этих значений в уравнение Ильковича дает

и после объединения констант

, (4.62)

т.е. диффузионный ток пропорционален корню квадратному от высоты ртутного столба.

Из сказанного следует важное для аналитической практики следствие: для определения концентрации вещества с одним и тем капилляром необходимо строго сохранять постоянной высоту ртутного столба.

Диффузионный ток согласно уравнению Ильковича зависит от величины , которая называется постоянной капилляра. Это также необходимо учитывать при проведении количественных анализов. Если регистрировать диффузионные токи одного и того же раствора вещества с помощью двух различных капилляров, то полученные токи будут относиться как

.

Следовательно, для сопоставления значений концентраций вещества, полученных с различными капиллярами, необходимо знать их периоды капания (t_max) и скорости вытекания ртути. При описании экспериментальных результатов следует указывать значения характеристик капилляра т и t_max, чтобы можно было сравнивать результаты, полученные c различными РКЭ.

Скорость вытекания ртути практически не зависит от потенциала, однако период капания заметно зависит от потенциала, причем эта зависимость имеет такой же вид, как и для поверхностного натяжения ртути. Графически изображенная зависимость периода капания от потенциала представляет электрокапиллярную кривую. Диффузионный ток имеет максимальное значение при потенциале электрокапиллярного нуля (нулевого заряда поверхности), а при более положительных или отрицательных потенциалах ток несколько уменьшается.

Повышение температуры вызывает увеличение диффузионного тока. Из величин, входящих в уравнение Ильковича зависят D, m и t_max. Для большинства ионов значения температурных коэффициентов диффузионного тока равны приблизительно 1,7 %. Хотя эти коэффициенты невелики, все же, чтобы ошибка в количественном анализе не превышала 1 %, необходимо поддерживать температуру электрохимической ячейки с точностью ±0,5^о.

Б 27.Миграционный ток и способы его подавления, полярографический «фон» .

движение иона осуществляются под действием миграционного тока f/х (градиента потенциала). Если скорость восстановления иона на поверхности значительно больше скорости движения, то на границе раздела происходит. (рис)

При некотором потенциале катода концентрация ионов у поверхности ртутной капли С_м уменьшается до ничтожно малой по сравнению с концентрацией в массе раствора, и скорость разряда ионов на катоде станет равной скорости диффузии. Поступление ионов к электроду может происходить не только в результате диффузии, но и за счет передвижения (мигрирования) ионов под влиянием наложенного электрического поля. Это дополнительное движение ионов затрудняет вывод количественных закономерностей при полярографическом анализе, поэтому миграцию ионов нужно свести к нулю. Резкое снижение миграции может быть осуществлено добавкой в раствор значительного избытка посторонних индифферентных ионов, которые восстанавливаются при более отрицательных потенциалах, чем определяемый ион, и поэтому не мешает процессу снятия полярограмм. Катионы фонового электролита экранируют электрод, уменьшая тем самым движущую силу миграции под действием электрического поля практически до нуля.

В качестве индифферентных электролитов, или иначе – фонов, особенно удобно применять соли, катионами которых являются ионы щелочных и щелочноземельных металлов, а анионами – перхлорат-, сульфат-, хлорат-ионы. Применяют и другие фоны: KCl, HCl, NaOH, NH₄Cl + NH₄OH (аммиачный буферный раствор) и др. Для определения щелочных металлов в качестве фона используют соли замещенного аммония, для которых потенциалы восстановления имеют еще более отрицательное значение, нежели для ионов щелочных металлов.

Значение фона не ограничивается только подавлением миграционного тока. Фон позволяет сильно увеличить электропроводность раствора, а также в результате комплексообразования он в ряде случаев раздвигает потенциалы полуволн определяемых ионов, поэтому становиться возможным из раздельное определение. Концентрация фона должна в 50-100 раз превышать концентрацию исследуемого вещества.

Кроме подбора определенного фона, для получения четких полярограмм необходимо из анализируемого раствора удалить растворенный в нем кислород. Дело в том, что кислород восстанавливается в две стадии: 1стадия  восстановление кислорода до перекиси водорода (Е_{1/2 (1)}=- 0,2 В); 2 стадия  восстановление перекиси (Е_{1/2 (2)} = - 0,9в), Концентрация растворенного в воде кислорода сопоставима с концентрацией определяемого полярографическим методом вещества, поэтому кислород сильно искажает нужные для определений полярограммы.

Б 28. Количественный полярографический анализ. Определение предельного диффузионного тока. Методы расчета концентрации деполяризаторов.

Наиболее широко применяется метод градировочного графика на основе уравнения: I_диф= К*С_0.

График строят по данным полярографирования нескольких стандартных растворов. На оси ординат откладывается пропорциональная силе диффузионного тока высота полярографической волны, а по оси абсцисс – концентрация анализируемого вещества.

В соответствии приведенным уравнением градуировочный график должен представлять прямую линию, проходящую через начало координат. К условия полярографирования относят условия работы капилляра, температуру и среду фоновый электролит). Метод градуировочного графика является наиболее трудоемким, но и наиболее точным.

Часто применяется менее трудоемкий метод- метод стандартных растворов. В этом методе в строго одинаковых условиях снимают полярограммы стандартного и анализируемого растворов и из пропорции, основанной на уравнении I_диф= К*С_0. ,рассчитывают неизвестную концентрацию С_х :

С_х=С_ст* (h_х/h_ст), где С_ст - концентрация стандартного раствора, h_х и h_ст – высота волны при полярографирования соответственно анализируемого и стандартного растворов.

Метод применим также только в условиях строгой стандартизации улсловий полярографирования.

Широко распространен метод добавок. Пусть при полярографировании исследуемого раствора сила диффузионного тока равна

I_x = К*С_х . добавим к этому раствору известное количество стандартного раствора С_ст и снова определим диффузионный ток: I_x+ст = К*(С_х+С_СТ).

Отсюда получаем:

С_х= С_ст*(I_x/I_x+ст-I_x)

По этому соотношению находим концентрацию анализируемого раствора. Можно использовать также графический метод. В этом случае полученные данные наносят на график зависимости I_x+ст от С_{ст .} при I_x+ст равное нулю. Следует,что С_х=-С _ст. то есть при экстраполяции прямая на этом графике при

I_x+ст равное нулю отсекает на оси абсцисс величину, равную концентрации определяемого вещества. В методе добавок автоматически учитывается влияние фона и так называемых третьих компонентов, что является важным достоинством метода, позволяющим применять его при анализе сложных смесей.

Б 29. Уравнение обратимой полярографической волны; потенциал полуволны и методы его определения; качественный полярографический анализ.

E = E⁰_1/2+ RT/nF ln I_диф-I/ I уравнение полярографической волны,где

E⁰_1/2 = E⁰ + RT/nF*ln (a_Hg_Mk_a)/ k_M_a.

E⁰_1/2 - потенциал этой полуволны

В начале процесса при небольшом потенциале катода сила тока медленно увеличивается с возрастанием потенциала- остаточный ток, его величина имеет порядок 10^-7 А. По достижении потенциала восстановления на катоде начинается разряд ионов и сила тока резко возрастает, стремясь к предельной величине диффузионного тока. При I= ½ I_d уравнение переходит в Е= E⁰_1/2 – это соотношение показывает независимость потенциала полуволны от силы тока и от концентрации восстанавливающегося иона. Потенциал полуволны является качественной характеристикой иона в растворе данного фонового электролита и определение потенциала полуволны составляет основу качественного полярографического анализа. Также потенциал полуволны зависит от среды, природы и концентрации фонового электролита. Особое значение имеет наличие в растворе веществ, способных к комплексообразованию с определяемым ионом. Присутствие в исследуемом растворе лиганда смещает потенциал полуволны в отрицательную область, что используется для определения состава и констант устойчивости координационных соединений. Если в растворе находится несколько веществ, потенциалы полуволны которых различаются на 100 милливольт и больше, то на полярограмме будет не одна волна, а несколько. Также возможно и больше, так как при ступенчатом восстановлении один ион может давать две волны.

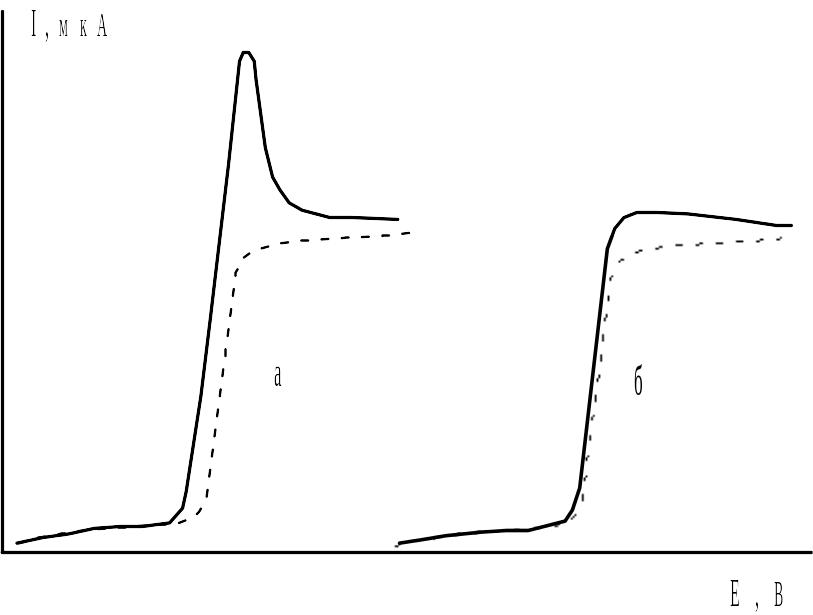
Б 30. Полярографические максимумы первого и второго рода; причины возникновения и методы подавления; использование максимумов для анализа ПАВ.

Зависимость силы тока от напряжения представляет собой полярографическую волну (полярограмму). На полярограммах нередко возникают максимумы различной формы, мешающие определению истинного потенциала полуволны и силы тока. Различают максимумы 1 и 2 рода. Теория связывает их появление с гидродинамическими явлениями в растворе, вызываемыми каплями ртути, и адсорбционными процессами. Для подавления максимумов в полярографируемый раствор обычно вводят ПАВ: желатин, агар-агар…подавление максимумов ПАВ лежит в основе нескольких чувствительных аналитических методик определения этих веществ в растворе(10^-9 моль на литр). Уравнение Ильковича связывает диффузионный ток с концентрацией иона и др. величинами:

I_диф = 605zD^1/2m^2/3t^1/6C₀ ,D – коэффициент диффузии, z-заряд иона, m-масса ртути, вытекающая из капилляра в 1 сек.,мг, t- время образования капли(переод капания).

Среди величин, входящих в это уравнение, труднее всего поддается экспериментальному определению коэффициент диффузии, а использование соответствующих справочных данных не всегда возможна. Поэтому коэффициент пропорциональности между концентрацией вещества и силой диффузионного тока обычно устанавливают с помощью стандартных растворов. Действительно, при постоянных условиях полярографирования D,m, t постоянны и уравнение переходит в I_диф= K *C₀.

В связи с этим в работах по полярографии всегда указывается характеристика капилляра, вычисляемая как m^2/3t^1/6. линейная зависимость является основой количественного анализа I_диф= K *C₀.

Причины возникновения максимумов второго рода - природа истечения ртутной капли. Устранить можно уменьшением размера ртутной капли(уменьшение диаметра капилляра) , с помощью принудительного отрыва капли или введением ПАВ, с увеличением концентрации которого величина мах уменьшается. Максимумы второго рода обычно не велики по амплитуде и размерам. Более ярко выражены мах первого рода(острые), причины возникновения которых являются электрокапиллярные явления( влияют поверхностное натяжение и ход течения капли).

Полярографические мах. Используются для определения содержания ПАВ в растворе- полярографический метод определения концентрации ПАВ(сначала строят градуировочный график , а потом находят концентрацию ПАВ в исследуемом растворе.

Рис. 7. Полярограммы с максимумами: а  первого рода; б – второго рода

Б 31. Дифференциальная постояннотоковая полярография.

В дифференциальной полярографии анализ ведется по полярографическим кривым dI/dE - E при сохранении потенциодинамического режима постояннотоковой полярографии. Для получения дифференциальных кривых dI/dE - E применяют три основных метода: графическое дифференцирование, полярографы с двумя синхронно капающими электродами и метод электрического дифференцирования. Полярографические кривые имеют острый максимум, положение которого на оси абсцисс определяется потенциалом полуволны, а высота - концентрацией анализируемого вещества. Дифференциальная полярография позволяет увеличить разрешающую способность метода по сравнению с прямой полярографией при сохранении практически прежней чувствительности (10^-5 моль/л).

(dI/ dE)_E=E1/2 = I_диф nF/4RT.

Величина точка мах на дифференциальной полярограмме пропорциональна силе диффузионного тока, она является мерой концентрации вещества. Получать дифференциальные полярограммы можно графическим дифференцированием обычных полярограмм или с помощью специальной электрической схемы, позволяющей непосредственно записывать дифференциальную кривую во время полярографирования. Дифференциальная полярография имеет значительно более высокую разрешающую способность, позволяя определять в одном растворе ионы с близкими потенциалами полуволны. Также этот метод более точен, так как фиксировать положение мах и измерять его высоту можно с более высокой точностью, чем определять аналогичные характеристики в методе обычной полярографии.

Б 32. ? Разностная и амальгамная полярографии.

Принцип метода разностной полярографии состоит в использовании двух ячеек с идентичными синхронно работающими капельными электродами. Одна из ячеек заполняется только фоном, другая фоном с анализируемым веществом. На обе ячейки подается одинаковое напряжение. Измеряется разность токов между двумя синхронно работающими РКЭ. Таким образом, на полярограмме регистрируются только волны, обусловленные восстановлением или окислением анализируемых веществ. Волна кислорода, волны веществ - микропримесей фона и емкостные токи взаимно компенсируются.

Использование метода разностной полярографии позволяет иногда повысить чувствительность на один - два порядка по сравнению с прямой полярографией, с сохранением разрешающей способности последней.

Для определения очень малых количеств вещества используется также инверсионная полярография. Она состоит в предварительном накоплении путем электролиза анализируемого вещества на электроде с последующим полярографированием. Этим методом возможно повысить чувствительность классической полярографии приблизительно на два порядка.

Б 33. Прямая амперометрия и амперометрические датчики.

Амперометрия – электрохимический метод анализа в котором приложены к ячейке потенциал поддерживается постоянным, а ток является функцией от концентрацией. Амперометрия делится на прямую и косвенную. Прямые амперометрические измерения применяют в амперометрических датчиках, которые имеют два электрода погруженных в электропроводящую среду. Один электрод индикаторный(рабочий), у него постоянный потенциал. Второй электрод- вспомогательный. Площадь рабочего электрода должна быть много меньше площади вспомогательного электрода тогда все приложенное напряжение пойдет на поляризацию рабочего электрода. Также можно использовать трехэлектродные датчики (с добавлением электрода сравнения).

Недостатки метода: метод малоселективен.

Б 34. амперометрическое титрование с одним заполяризованным электродом; форма кривых титрования; амперометрические индикаторы.

Процесс амперометрического титрования основан на измерении силы тока при напряжении, соответствующем величине предельного тока после прибавления порции реактива. По полученным данным строят кривую амперометрического титрования в координатах сила тока - объем титранта и графически находят точку эквивалентности. В качестве индикаторного электрода применяют вращающиеся платиновые, графитовые и другие твердые электроды. Вид кривой амперометрического титрования зависит от того, какой компонент реакции титрования вступает в электродную реакцию – определяемое вещество, титрант или продукт реакции.

3 рисунка.

I_d I_d

V_т.э. V V_т.э. V

а б

Рис. 1. Кривые амперометрического титрования: а  электрохимически активно определяемое вещество; б  электрохимически активен титрант

I_d I_d

а б

V_т.э. V V_т.э. V

Рис. 2. Кривые амперометрического титрования: а  электрохимически активен только продукт реакции; б  электрохимически активны определяемое вещество и титрант.

Если на рабочем электроде при заданном потенциале возможно восстановление (или окисление) определяемого вещества и титранта, то наблюдаются V образные кривые титрования,

В методах А.Т. применяют реакции осаждения, комплексообразования и ОВР.

Необходимо, чтобы реакция, протекающая при АТ, удовлетворяла тем требованиям, которые предъявляются к реакциям в титриметрических методах в отношении полноты и скорости их протекании.