ANSYS Mechanical

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

Эквивалентно измененные общие деформации определяются следующим образом:

4.3.9.3 Вязкопластичность

Вязкопластичность является формой пластичности, зависящей от времени, где развитие пластических деформаций зависит от скорости приложения нагрузки. Простейшим применением вязкопластичности является процесс высокотемпературной формовки металла, такой, как прокатка и глубокая вытяжка, вызывающие большие пластические деформации и перемещения с малыми упругими деформациями.

Вязкопластичность моделируется типами элементов VISCO106, VISCO107 и VISCO108, использующими для описания свойств материала модель Ананда (Anand).

Вязкопластичность определяется объединением пластичности и ползучести посредством набора пластических деформаций и эволюционных уравнений. Для сохранения объема в области пластичности используется уравнение ограничений.

Опция пластичности, зависящей от скорости деформации (вязкопластичности) или

TB,RATE позволяет вводить эффект скорости изменения деформаций в модели материалов для моделирования отклика материала, зависящего от времени. Применяются две опции материала, модель Пежины (Perzyna) и модель Пирса (Peirce). В отличие от других опций зависящего от скорости деформации материала, имеющихся в комплексе ANSYS, таких, как ползучесть или модель Ананда (Anand), модели Пежины (Perzyna) и Пирса (Peirce) также включают поверхность пластичности. Пластичность, и, таким образом, эффект упрочнения, связанный со скоростью деформаций, активизируется только после пластического деформирования. Для моделирования вязкопластичности требуется использовать модели в комбинации с опциями материала BISO, MISO или NLISO. Кроме того, анизотропная вязкопластичность может комбинироваться с опцией HILL.

Модель Пежины (Perzyna)

Для данной модели напряжения текучести материала рассчитываются по формуле:

σ = 1+ εγpl m σ0

где:

σ– напряжение текучести материала (material yield stress);

εpl – эквивалентный коэффициент пластической деформации (equivalent plastic strain rate);

m – параметр ужесточения коэффициента деформаций (strain rate hardening parameter); γ – вязкость материала;

σ0 – статическое напряжение текучести материала (static yield stress of material), зависит от некоторых параметров ужесточения (hardening).

Решение сходится к статическому при γ → ∞ , или при m → 0 , или при ε pl → 0 . Однако для данной модели материала при m<0,1 сходимость достигается плохо.

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

Модель Пирса (Peirce)

Для данной модели материала напряжения рассчитываются по формуле:

σ = 1 + εγpl m σ0

Как и для модели Пежины (Perzyna) решение сходится к статическому при γ → ∞ , или при

m → 0 , или при ε pl → 0 . Однако при малых значениях m сходимость достигается намного лучше.

Модель Ананда (Anand)

Существуют два основных признака, характеризующих модель пластического поведения Ананда применительно к изотропным металлам. Во-первых, отсутствует задаваемая в явном виде поверхность текучести, отклик материала зависит от его текущего напряженного состояния. Во-вторых, для описания изотропного сопротивления неупругому течению материала используется единственная внутренняя скалярная переменная "s", называемая деформационным сопротивлением. Наличие этих особенностей находит отражение в определяющих уравнениях модели; одно из них записывается в виде уравнение течения:

другое – как уравнение, описывающее изменение с течением времени деформационного сопротивления:

Последнее уравнение позволяет моделировать не только упрочнение материала, но и снижение сопротивления с ростом деформаций:

B =1− ss*

dp – эффективный коэффициент неупругой деформации (effective inelastic deformation rate); σ – эффективное напряжение Коши;

s – деформационное сопротивление (deformation resistance);

s* – порог насыщения (saturation value) деформационного сопротивления; θ – абсолютная температура.

4.3.9.4 Нелинейная упругость

ПК ANSYS предусматривает возможность моделировать материалы с нелинейными (полилинейными) упругими свойствами. В таких случаях в отличие от пластического поведения материала энергия деформирования сохраняется (процесс консервативен).

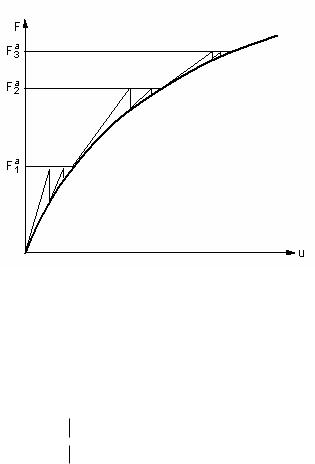
Учет такого поведения материала выполняется с помощью команды TBPT с опцией TB,MELAS для соответствующих конечных элементов. На Рис. 4.8 показаны основные черты нелинейноупругого поведения материала. Следует обратить внимание на то, что

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

материал разгружается по кривой нагружения, при этом остаточные неупругие деформации не возникают.

Рис. 4.8 Кривая “напряжение-деформация” для нелинейной упругости

Величина общей деформации {εn} используется для вычисления суммарной эквивалентной деформации:

напряжений σе.

Упругая (линейная) составляющая деформации может быть вычислена с помощью соотношения:

{εnel }= Eσεeet {εn }

поэтому “пластическая” или нелинейная часть деформации:

{εnpl }= {εn }−{εnel }

Чтобы избежать образования несимметричной матрицы, используется только симметричная часть матрицы касательной жесткости для соотношений “напряжениедеформация”:

которая представляет собой матрицу секущей жесткости для кривой “σ – ε”.

4.3.9.5 Гиперупругость

Гиперупругость характеризует поведение материалов, которые могут испытывать полностью обратимые конечные упругие деформации. К таким материалам относятся резины и многие другие полимерные материалы. Напряжения в них обычно являются

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

функцией плотности энергии деформирования. В ANSYS предусмотрены следующие варианты описания поведения гиперупругих материалов:

•Модель Нео-Хукина (Neo-Hookean);

•Модель Муни-Ривлина (Mooney-Rivlin);

•Полиномиальная форма (Poiynomial Form);

•Модель Огдена (Ogden Potential);

•Модель Арруда-Бойса (Arruda-Boyce);

•Модель Гента (Gent);

•Модель Йео (Yeoh);

•Модель Огдена для сжимаемых вспененных или им подобным материалов (Ogden Compressible Foam Model);

•Модель Блатц-Ко (Blatz-Ko Model).

Материал считается гиперупругим, если существует функция упругого потенциала W (или функция плотности энергии деформации), которая является скалярной функцией тензора деформации или тензора перемещения, производная которой по компонентам деформации определяет соответствующий компонент напряжения. Выражение может иметь вид:

Sij = ∂W = 2∂W

∂Eij ∂Cij

где:

Sij – компоненты второго тензора напряжений Пиолы – Кирхгофа (Piola-Kirchhoff); W – функция энергии деформации на единицу недеформированного объема;

Eij – компоненты тензора деформации Лагранжа;

Cij – компоненты правого тензора деформации Коши-Грина.

Деформации Лагранжа определяются следующим образом:

Eij = 0.5(Cij −δij )

где δij = 1.0 при i = j и δij = 0.0 при i ≠ j.

Тензор деформаций Cij определяется произведением градиентов деформации fij:

Cij = fik fkj

где:

fij = ∂Xi /∂xi;

Xi – недеформированное положение точки в направлении i;

xi = Xi + ui – деформированное положение точки в направлении i; ui – перемещение точки в направлении i.

Теория, используемая для семейства гиперупругих конечных элементов, применима только для изотропных материалов. При этом, однако, никаких ограничений на величину деформаций не накладывается, а результаты не зависят от пути нагружения.

В рамках настоящей верификации рассматриваются гиперупругие модели Муни-

Ривлина (Mooney-Rivlin) и Огдена (Ogden Potential).

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

Определяющее соотношение Муни-Ривлина (Mooney-Rivlin) представляет собой разумную модель поведения для некоторых почти несжимаемых натуральных резиноподобных материалов. Функция плотности энергии деформаций для модели МуниРивлина с параметром 2 имеет следующее выражение:

W = c10 (I1 −3)+ c01 (I2 −3)+ d1 (J −1)2

где:

Ii – редуцированные инварианты деформации в i-ом направлении, заданные следующим

образом:

I1 = I1 I3-1/3

I2 = I2 I3-1/3 I3 = I31/2

с10, с01, d – константы материала;

Ii – инварианты правого тензора деформации Коши-Грина Cij:

I1 = Cii

I2 = Ѕ (I12 - Cij Cij)

I3 = det Cij – коэффициент изменения объема.

Для модели Муни-Ривлина с 5-ю параметрами функция плотности энергии деформации вычисляется:

W = c10 (I1 −3)+ c01 (I2 −3)+ c20 (I1 −3)2 + c11 (I1 −3)(I2 −3)+ c02 (I1 −3)2 + d1 (J −1)2

где с10, с01, с20, с02, d – константы материала.

Для модели Муни-Ривлина с 9 параметрами функция плотности энергии деформации вычисляется:

W = c10 (I1 −3)+ c01 (I2 −3)+ c20 (I1 −3)2

+ c11 (I1 −3)(I2 −3)+ c02 (I1 −3)2 + c30 (I1 −3)3

+ c21 (I1 −3)2 (I2 −3)+ c12 (I1 −3)(I2 −3)2 + c03 (I2 −3)3 + d1 (J −1)2

где с10, с01, с20, с02, с03, с30, с11, с12, с21, d – константы материала.

Заметим, что для малых деформаций выражение 2(с10 + с01) представляет собой модуль сдвига, а выражение 6(с10 + с01) – модуль Юнга.

Начальный модуль объемной деформации K (bulk modul) определяется выражением:

где:

µn, αn, dk – константы материала; J – третий инвариант тензора деформаций.

В силу трудоёмкости вычисления констант материала значение N не рекомендуется задавать больше 3.

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

Начальный модуль сдвига µ определяется выражением:

µ = 1 ∑N αi µi

2 i=1

Начальный модуль объемной деформации K (bulk modul) определяется выражением:

K = 2 d1

4.3.9.6 Моделирование бетона

Модель популярного строительного материала – бетона – прогнозирует разрушение хрупких материалов. Учитываются как механизмы трещинообразования, так и разрушения при дроблении. Команда TB,CONCR позволяет использовать эту модель материала, которая применяется вместе с конечным элементом железобетона SOLID65.

Критерий разрушения бетона при сложном напряженном состоянии может быть выражен следующим образом:

F − S ≥ 0 fc

где:

F – функция состояния главных напряжений (σxp, σyp, σzp);

S – поверхность разрушения, выраженная в компонентах главных напряжений и пятью

параметрами ft, fc, fcb, f1 и f2;

fc – предельная прочность при одноосном сжатии;

ft – предельная прочность при одноосном растяжении; fcb – предельная прочность при двухосном растяжении;

f1 – предельная прочность при двухосном сжатии, наложенном на гидростатическое напряжение σha;

f2 – предельная прочность при одноосном сжатии, наложенном на гидростатическое напряжение σha;

σha – среднее (гидростатическое) напряжение;

σxp, σyp, σzp – главные напряжения для главных направлений.

Если условие критерия разрушения не выполняется, то растрескивания, раздробления не происходит. И наоборот, материал будет растрескиваться, если любое из главных напряжений является растягивающим, и будет раздавливаться, если все главные напряжения оказываются сжимающими.

Для задания поверхности разрушения и определения величины среднего (гидростатического) напряжения требуется введение пяти параметров (каждый из которых может зависеть от температуры), представленных выше.

Между тем, поверхность разрушения может быть задана с использованием двух констант ft и fc. Другие три константы задаются по умолчанию [37]:

fcb = 1,2 fc; f1 = 1,45 fc; f2 = 1,725 fc.

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

Однако эти значения по умолчанию имеют силу только для напряженного состояния, когда выполняется условие:

σh ≤ 3 fc

σh = 13 (σxp +σyp +σzp ) – среднее, или гидростатическое, напряжение.

Таким образом, это условие используется в тех случаях, когда компоненты гидростатического напряжения достаточно малы. Все пять параметров разрушения задаются в ситуации, когда предполагаются большие значения составляющих гидростатического напряжения. Если оно не выполняется и принимаются значения параметров по умолчанию согласно выше обозначенным соотношениям, оценка прочности бетона может оказаться ошибочной.

Как функция F, так и поверхность разрушения S выражаются в компонентах главных напряжений, обозначенных σ1, σ2, σ3, при этом главные напряжения удовлетворяют условиям:

σ1 = max (σxp , σyp , σzp), σ3 = min (σxp , σyp , σzp),

и σ1 ≥ σ2 ≥ σ3.

Разрушение бетона может произойти в следующих четырех случаях:

•0 ≥ σ1 ≥ σ2 ≥ σ3 (сжатие-сжатие-сжатие);

•σ1 ≥ 0 ≥ σ2 ≥ σ3 (растяжение-сжатие-сжатие);

•σ1 ≥ σ2 ≥ 0 ≥ σ3 (растяжение-растяжение-сжатие);

•σ1 ≥ σ2 ≥ σ3 ≥ 0 (растяжение-растяжение-растяжение).

В каждой такой области для описания поверхностей F и S используются независимые функции. Четыре функции, составляющие общую поверхность F, обозначаются F1, F2, F3 и F4; функции, составляющие общую поверхность S, обозначаются S1, S2, S3 и S4. Функциям Si (i = 1,4) присуще свойство, в соответствии с которым представляемая ими поверхность является непрерывной, при этом градиент поверхности не остается непрерывным, если любое главное напряжение меняет знак. Для каждого из четырех случаев критерий разрушения и поверхность разрушения подробно обсуждаются в [16].

4.3.10Нелинейные статические и динамические задачи

Конечноэлементная дискретизация дает следующую нелинейную систему уравнений:

производных;

{u} – вектор неизвестных степеней свободы; {F a }– вектор приложенных нагрузок.

Методом решения нелинейных уравнений является итерационный метод НьютонаРафсона и его варианты (модификации).

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

4.3.10.1 Метод Ньютона-Рафсона

Метод Ньютона-Рафсона описывается соотношениями:

– матрица Якоби (тангенциальная); i – номер текущей итерации;

{Fi nr } – вектор восстанавливающей нагрузки, соответствующий элементной инерционной нагрузке.

Рис. 4.9 иллюстрируют определение значений матрицы [Ki ]T и вектора {Fi nr }.

Рис. 4.9 Геометрическая интерпретация метода Ньютона-Рафсона

Для задач с учетом нелинейности, зависящей от “пути” нагружения (например, пластичности), требуется нагрузку {F a }задавать пошагово (Рис. 4.10):

где:

[Kn,i ]T –тангенциальная (касательная ) матрица для n-го шага по времени и i-ой итерации; {Fn a }– полный вектор приложенной нагрузки на n-ом шаге по времени;

{Fn,i nr } – вектор восстанавливающей нагрузки, соответствующий элементной инерционной нагрузке на n-ом шаге по времени и i-ой итерации.

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

Рис. 4.10 Геометрическая интерпретация шагового (инкрементного) метода Ньютона-Рафсона

Когда матрица жесткости обновляется на каждой итерации, тогда речь идет о полном методе Ньютона-Рафсона. Альтернативными являются модифицированный метод и схема с начальной жесткостью.

Сходимость достигается при условии:

где:

{R}= {F a }−{F nr }

4.3.10.2 Метод окаймляющих дуг (arc-length method)

Метод окаймляющих дуг применим для решения задач статики (нелинейная потеря устойчивости) с большой геометрической нелинейностью, включая учет закритического поведения [173]. Метод Ньютона-Рафсона является основой для метода окаймляющих дуг. Уравнение (100) запишем иным образом:

где:

∆λ – приращение фактора нагрузки (Рис. 4.11)

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

Рис. 4.11 Геометрическая интерпретация метода окаймляющих дуг совместно с методом Ньютона-Рафсона

Приращения перемещений {∆ui } могут быть выражены:

где:

{∆ui I }= [KiT ]−1 {F a }– перемещения от единичного фактора нагрузки;

{∆ui II }= −[KiT ]−1{Ri } – приращения перемещений для метода Ньютона-Рафсона.

где:

β – коэффициент масштабирования (в единицах перемещений); ∆un – сумма всех приращений ∆ui на данной итерации.

существует много методов аппроксимации ∆λ . В явном виде сферический итерационный метод используется для обеспечения ортогональности [173]. Сначала вычисляется необходимый остаточный радиус ri для явной итерации на сфере. Затем, определяется ∆λ

по формуле: