ANSYS Mechanical

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

где:

f jc – комплексная амплитуда силы;

Ω – заданная круговая частота. Аналогично выразим

где:

y jc – комплексная амплитуда модальной координаты для j-й формы колебаний.

Продифференцировав уравнение (44), подставив выражения (43) и (44) в (41), выполнив ряд несложных преобразований, решим (41) относительно y jc :

Вклад каждой формы колебаний выражается формулой (46):

где:

{C j }– вклад j-й формы колебаний; {φj }– j-я форма колебаний.

В итоге, искомый вектор комплексных перемещений {uc } для n форм колебаний можно выразить следующим образом:

j=1

4.3.6 Спектральный динамический (сейсмический) анализ

Спектральными расчетами называются расчеты, в которых результаты расчета собственных колебаний используются совместно с заранее известным спектром возбуждения для определения перемещений, деформаций, усилий и напряжений системы. Эти расчеты альтернативны расчетам динамических процессов с известной историей нагружения во времени для определения отклика конструкции на приложение случайных или независящих от времени нагрузок (сейсмические, ветровые и т. д.).

Спектром называется функциональная зависимость каких-либо характеристик от частоты, включающая интенсивность и частотный состав при нагружении, зависящем от времени. При проведении спектральных расчетов применяются три перечисленных ниже метода:

•Спектральный отклик:

•Спектральный отклик с возбуждением по “платформенной” (одноточечной)

схеме (Single-Point Response Spectrum, или SPRS);

•Спектральный отклик при “многоточечном” возбуждении (Multi-Point Response Spectrum Method, или MPRS);

•Динамический метод (Dynamic Design Analysis Method, или DDAM);

•Cпектральной плотности мощности (Power Spectral Density, или PSD)

Метод спектрального отклика и динамический метод являются детерминированными, поскольку оба они применимы для обработки как входных, так и выходных данных действующих значений величин. Расчет же случайных колебаний является по своей природе

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

вероятностным (недетерминированным), поскольку и входные, и выходные значения представляют собой вероятностные оценки величин.

Остановимся на рассмотрении спектрального отклика с возбуждением по “платформенной” схеме (SPRS) и спектральной плотности мощности (PSD).

4.3.6.1Спектральный отклик с возбуждением по “платформенной” схеме (Single-Point Response Spectrum, или SPRS)

Спектральным откликом является отклик системы с одной степенью свободы на функцию нагружения, зависящую от времени. Она является графиком отклика в зависимости от частоты, где отклик может являться перемещением, скоростью, ускорением или усилием.

При расчетах спектров по “платформенной” схеме возбуждения (SPRS) определяется одна кривая отклика (или семейство кривых) для набора точек модели, таких, как все опоры, как показано на Рис. 4.1.

Рис. 4.1 Спектр возбуждения по “платформенной” схеме

Процедура расчета спектральных задач по “платформенной” схеме возбуждения сводится к четырем основным шагам:

1.Проведение расчета собственных форм и частот (см. раздел 3.3.3).

2.Проведение расчета спектральных характеристик:

Применяются перечисленные ниже опции:

•Типа спектра отклика (перемещения, скорости, ускорения, усилия или PSD). Все спектры, за исключением спектра усилия, являются сейсмическими спектрами (команда

SVTYP).

•Направление возбуждения (команда SED)

где:

{D}= [D1a D2a D3a ...]T

D aj – направление возбуждения в j-й опоре вдоль оси a – X, Y или Z, или поворот вокруг этих осей.

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

X, Z, Y – текущие координаты в глобальной декартовой системе координат;

X0, Z0, Y0 – координаты точки, относительно которой происходит поворот в глобальной декартовой системе координат;

{e} – шесть возможных единичных векторов.

•Указание значений в точках спектра или кривой по частотам.

Если задан более чем один вид демпфирования, комплекс ANSYS вычисляет эффективный коэффициент демпфирования для каждой i-й частоты

j=1

где:

β– демпфирование, связанное с жесткостью;

ωi –собственная круговая частота i-й формы колебаний недемпфированной системы;

ξc – постоянный коэффициент демпфирования;

Таблица модальных коэффициентов содержит список коэффициентов вкладов, коэффициентов форм (рассчитанных при минимальном коэффициенте демпфирования) и распределение масс для каждой формы. Для вычисления максимального отклика на каждой форме (частотного отклика) имеющиеся значения расчетных объектов для формы умножаются на коэффициенты форм.

3.Расширение форм (если собственные формы определялись методом редукции).

4.Комбинирование форм.

4.3.6.2Спектральная плотность мощности, СПМ (Power Spectral Density, PSD)

Метод спектральной плотности мощности (СПМ) является статистической оценкой величины среднеквадратического значения случайной переменной. Метод используется для

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

расчета случайных колебаний, в которых значения отклика могут быть определены только в виде функций распределения вероятности.

Метод СПМ является статистической мерой отклика модели на случайные динамические условия нагружения. Метод определяет связь спектральной плотности с частотой, причем можно определить плотность спектра перемещений, скоростей, ускорений и усилий. Математически площадь под кривой связи спектральной плотности с частотой равна вариации (квадрату стандартного отклонения отклика).

Подобно расчетам спектров отклика, расчет случайных колебаний может иметь характер возбуждения с единичной точкой и несколькими точками. При расчете случайных колебаний с одной точкой возбуждения для всей модели указывается единый спектр плотности возбуждения. При расчете случайных колебаний с несколькими точками возбуждения для разных точек модели указываются разные плотности спектра возбуждения.

Процедура определения отклика PSD состоит из четырёх основных этапов:

1.Проведение расчёта собственных колебаний (см. раздел. 3.3.3).

2.Расширение форм (если собственные формы определялись методом редукции)

3.Проведение расчёта спектральных характеристик:

4.Комбинирование форм.

Для частично коррелированных узловых и базовых возбуждений полные уравнения движения для свободных (f) и закрепленных (r) степеней свободы разделяются:

4.3.7Прямой динамический расчет

Для линейных задач динамики рассматривается следующая система уравнений:

где:

[M ] – матрица масс системы;

[C] – матрица демпфирования (диссипации) системы; [K ]– матрица жесткости системы;

{u} – вектор узловых ускорений; {u} – вектор узловых скоростей; {u} – вектор узловых перемещений;

{F a }– функция нагрузки, зависящая от времени.

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

Матрица жесткости определяется выражением:

N

[K ]= ∑[Ke ]

m=1

где:

N – число элементов

[Ke] – матрицы жесткости отдельных элементов. Матрица масс системы определяется соотношением:

N

[M ]= ∑[Me ]

m=1

где:

[Me] – матрицы масс отдельных элементов.

В программе ANSYS матрица масс элемента может представлять собой согласованную матрицу, матрицу сосредоточенных масс (диагональную) или редуцированную (приведенную) матрицу.

Согласованная матрица масс элемента вычисляется с использованием функций формы элемента. Эти функции формы аналогичны используемым при вычислении матрицы жесткости, т.е. являются согласованными.

B матрице сосредоточенных масс масса каждого элемента распределяется (не обязательно поровну) по его узлам. Другими словами, сосредоточенные массы, размещенные в узлах элемента, в сумме равны массе элемента. Поэтому матрица сосредоточенных масс является диагональной, т.е. все элементы матрицы, кроме диагональных, равны нулю. Сумма “узловых” масс в каждом отдельном направлении равна общей массе элемента. (Опция назначается командой LUMPM, ON).

Ряд конечных элементов программы ANSYS (например, BEAM44, PIPE59, SHELL63) имеют опцию KEYOPT, позволяющую использовать редуцированную матрицу масс элемента. Эта матрица образуется исключением из согласованной матрицы тех ее элементов, которые относятся к вращательным степеням свободы.

Большинство конечных элементов программы ANSYS используют по умолчанию согласованную матрицу масс. В общем случае рекомендуется использовать матрицу масс, заданную по умолчанию, за исключением следующих случаев:

•если объект расчета имеет относительно малый размер в одном (или двух) направлениях по сравнению с остальными размерами (например, тонкие балки или очень тонкие оболочки), то следует использовать опцию редуцированной матрицы масс (если доступна) или опцию матрицы сосредоточенных масс;

•для некоторых задач распространения волн более эффективным оказывается использование матрицы сосредоточенных масс.

Полное выражение для матрицы демпфирования [C] может быть записано следующим образом:

где:

α и β – константы демпфирования Релея; NMAT – число материалов в модели;

ξ – постоянный коэффициент затухания;

[Cξ] – частотно-зависимая матрица демпфирования; [Ck] – матрица сопротивления отдельного элемента; NEL – число элементов с демпфирующими свойствами; α[M ] – инерционное демпфирование;

[K ] NMAT j [K j ] – конструкционное демпфирование;

β + ∑β

j=1

[Cξ ]– постоянное демпфирование;

NEL

∑[Ck ] – элементы с трением.

k =1

Разрешающая система уравнений (54) решается методом Ньюмарка или методом HHT (Hilbert-Hughes-Taylor) с процедурой пошагового нагружения по времени для неявных схем интегрирования уравнений движения.

Всвою очередь, существуют три способа решения метода Ньюмарка:

•полный метод (Full Solution Method)

•редуцированный (Reduce Solution Method)

•метод суперпозиций (Mode superposition Method)

Для метода HHT доступен лишь Full Solution Method.

4.3.7.1 Метод Ньюмарка (The Newmark method)

Метод Ньюмарка основан на методе конечных разностей для интервала времени ∆t, когда предполагается, что

где:

α, δ – параметры Ньюмарка, выбираемые из условия получения оптимальной устойчивости и точности. Ньюмарк предложил в качестве безусловно устойчивой схемы метод постоянного среднего ускорения, для которого δ = 0,5 и α = 0,25.

∆t = tn+1 −t n ;

{un } – вектор узловых перемещений в момент времени tn; {un } – вектор узловых скоростей в момент времени tn; {un } – вектор узловых ускорений в момент времени tn;

{un+1} – вектор узловых перемещений в момент времени tn+1; {un+1} – вектор узловых скоростей в момент времени tn+1; {un+1} – вектор узловых ускорений в момент времени tn+1.

Поскольку основной целью является вычисление перемещений {un+1}, поэтому

С учетом уравнений (58) и (59) уравнение равновесия (57) можно записать следующим образом:

Метод Ньюмарка с коэффициентами δ = 0,5 и α = 0,25 (метод постоянного среднего ускорения или трапециедальный метод) безусловно устойчив и не вносит в результаты дополнительного численного демпфирования. Однако этот метод вызывает удлинение периодов собственных колебаний.

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

4.3.7.2 Метод Хильбера–Хьюза (HHT, Hilber-Hughes-Taylor)

Метод Хильбера–Хьюза (HHT) при параметре γ = 0 эквивалентен методу Ньюмарка в форме постоянного среднего ускорения. Численное демпфирование при использовании этого метода является функцией параметра γ.

Уравнение равновесия имеет вид:

αm и αf два дополнительных параметра интегрирования для интерполяции ускорения и перемещения, скорости и нагрузок.

Уравнение равновесия относительно {un+1} можно переписать в виде (62):

(a0 [M ]+ a1 [C]+ (1−α f ) [K ]) {un+1}= (1−α f ) {Fna+1}+α f {Fna }−α f {Fnint }+

[M ] (a0 {un }+ a2 {un }+ a3 {un })+[C] (a1 {un }+ a4 {un }+ a5 {un })

где:

4.3.8 Геометрическая нелинейность (включая устойчивость)

Изменение геометрической формы конструкции при появлении значимых перемещений вызывает нелинейный отклик (геометрическая нелинейность). То есть, жесткость [K] является функцией перемещения {u}. Геометрическая нелинейность характеризуется большими перемещениями и (или) поворотами. Виды геометрической нелинейности, рассмотренные в настоящей верификации:

Большие деформации (Large strains) предполагают, что деформации не являются бесконечно малыми (являются конечными). Изменения формы (например, площади поперечных сечений, толщины и т.д.) также учитываются. Перемещения и повороты могут быть произвольными.

Большие смещения (Large dispacements) предполагают, что повороты являются большими, но механические деформации (вызывающие напряжения) оцениваются при помощи линеаризованных выражений. Конструкция считается не изменяющей форму, за исключением случая движения в виде жесткого целого. Элементы этого класса соответствуют своей первоначальной форме.

Ужесточение при нагружении (Stress-Stiffening) предполагает, что и деформации, и повороты являются малыми. Для учета отдельных нелинейных эффектов поворотов используется аппроксимация первого порядка.

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

4.3.8.1 Большие деформации

Если деформации в материале превышают несколько процентов, изменением геометрии, связанным с деформациями, нельзя пренебрегать.

Задача вычисления больших деформаций может быть решена путем определения некоторых основных физических величин (движения и деформации) и соответствующих математических соотношений. Приложенные нагрузки, действующие на тело, приводят его в движение из одного положения в другое. Это движение может быть определено путем изучения положений радиус-векторов в деформированном {x} и недеформированном {X} состоянии. Затем вычисляется вектор движения (перемещения) {u}:

Градиент деформаций определяется как:

Градиент деформации содержит информацию об изменении объема, углов поворота и формы деформированного тела. Изменение объема в точке:

где:

V0 – исходный объем;

V – текущий объем.

Градиент деформации может быть разделен на изменение угла поворота и изменение формы с помощью теоремы правого полярного разложения:

где:

[R] – матрица поворота;

[U] – матрица изменения формы (растяжения).

После того, как матрица растяжения вычислена, логарифмическая оценка деформаций Генки определяется как:

[ε] здесь выражено в тензорной форме, в отличие от обычной векторной формы {ε}.

Начиная с [U] тензора второго порядка, (67) определяется на основе спектрального разложения [U]:

i=1

где:

λi – собственные значения [U] (основные растяжения); {ei} –собственные векторы [U] (основные направления).

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1

4.3.8.2 Большие смещения

Для решения задач с большими деформациями ранее была описана теория общего движения материальной точки. Теория решения задач с большими смещениями и углами поворота аналогична, за исключением того, что логарифмическая мера деформаций заменяется на меру Био (Biot) или меры малых деформаций:

где:

[U] – матрица изменения формы (растяжения); [I] – единичная матрица 3×3.

4.3.8.3 Ужесточение при нагружении

Ужесточение при нагружении – увеличение жесткости в напряженном состоянии. Этот эффект, как правило, необходимо учитывать при расчете конструкций, жесткость которых на изгиб значительно меньше осевой жесткости. Например, таковы вантовые системы, тонкие балки, оболочки и т.п. Кроме того, этот эффект увеличивает размерность нелинейной матрицы жесткости, вызванной большими деформациями или большими перемещениями. Влияние ужесточения при нагружении учитывается путем генерации и использования дополнительной матрицы жесткости, в дальнейшем называемой матрицей геометрической жесткости (stress stiffness). Эта матрица добавляется к основной матрице жесткости, чтобы увеличить полную жесткость системы. Матрица геометрической жесткости вычисляется исходя из напряженного состояния конструкции на предыдущей равновесной итерации. Таким образом, для получения решения задачи с ужесточением при нагружении необходимо не менее двух итераций. На первой итерации определяется напряженное состояние системы, которое будет использовано для формирования матрицы геометрической жесткости на второй итерации. Если дополнительная жесткость влияет на напряжения в системе, то для получения решения необходимо провести ещё несколько итераций.

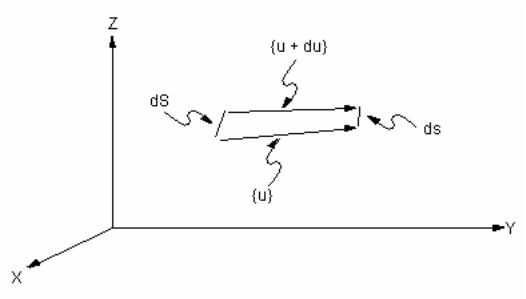
Ниже приведен вывод выражения перемещений-деформаций для общего случая движения дифференциального длинного волокна.

Рис. 4.2 Общей случай движения волокна