1.5 Основные законы и уравнения электрических цепей
Основными физическими законами, позволяющими описать любые режимы электрической цепи, являются законы Ома.
1. Закон Ома для участка цепи, не содержащего ЭДС, устанавливает связь между током и напряжением на этом участке (рис. 1.13)
2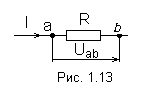
.
Закон Ома для участка цепи, содержащего
источник ЭДС
(обобщённый закон Ома)
Обобщённый закон Ома позволяет найти ток этого участка по известной разности потенциалов на концах участка цепи и имеющейся на этом участке ЭДС E.
И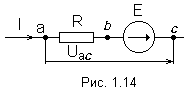
мея
в виду, что в неразветвлённом участке
электрической схемы с произвольным
числом ЭДС, сопротивлений и заданной
разностью потенциалов на его концах,
ток направлен от высшего потенциала к
низшему.
Если
предположить, что
,
то ток и напряжение будут направлены
от точки а
к точке с.
(рис. 1.14).
;
(1.29)
.
(1.30)
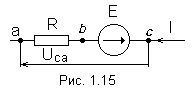
Если
предположить, что
,
то ток и напряжение будут направлены
от точки с к точке а, напряжение
и ток определим по формуле 1.29 -1.30.
(рис. 1.15).
|
|
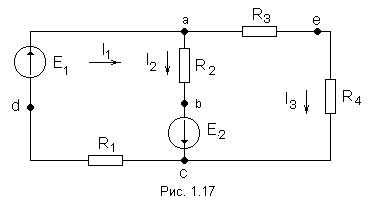
Основными уравнениями теории электрических цепей являются уравнения Кирхгофа, поэтому все электрические цепи подчиняются первому и второму законам Кирхгофа.
Оба эти закона установлены на основе многочисленных опытов и являются следствием закона сохранения энергии.
П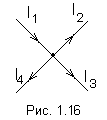
ервый
закон Кирхгофа можно сформулировать
двояко:
Алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю:
.
(1.31)
(Подтекающие к узлу токи считаются положительными, а утекающие – отрицательными).
Сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов:
.
(1.32)
Второй закон Кирхгофа можно также сформулировать двояко:
Алгебраическая сумма напряжений (не падений напряжений) вдоль любого контура равна нулю
,
(1.33)
.
Алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
.
(1.34)
При составлении уравнений слагаемые берут со знаком плюс, если действующие на участках напряжения и ЭДС совпадают с направлением обхода, и со знаком минус, если их действия противоположны направлению обхода.
При составлении уравнений для расчёта токов в схемах с помощью законов Кирхгофа необходимо придерживаться следующего алгоритма:
Произвольно задаются положительные направления токов.
Произвольно задаются положительные направления обхода контуров (с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми, например, по часовой стрелке).
Составляют уравнения по первому закону Кирхгофа. Число таких уравнений должно быть на единицу меньше числа узлов.
Недостающие уравнения составляют по второму закону Кирхгофа, при этом учитывают, чтобы в каждый новый контур входила, хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых записаны уравнения.
Решая полученную систему уравнений, находим неизвестные токи. Если какой - то ток или несколько токов, оказались отрицательными, то это значит, что действительное направление этих токов противоположно выбранному.