§17. Исследование уравнения гиперболы

Пусть гипербола задана каноническим уравнением

, (1)

где с² = а²+b² . (2)

1. Оси и центр

Как и в случае эллипса доказывается, что гипербола с уравнением (1) симметрична относительно осей координат и начала координат.

Определение 1. Центр симметрии гиперболы называется её центром, оси симметрии – осями. Ось гиперболы, на которой лежат её фокусы, называется фокальной осью.

2. Вершины

1. Найдём точки пересечения гиперболы с осью Ох:

A₁(a;0), A₂(-a;0).

2. Найдём точки пересечения гиперболы с осью Оy:

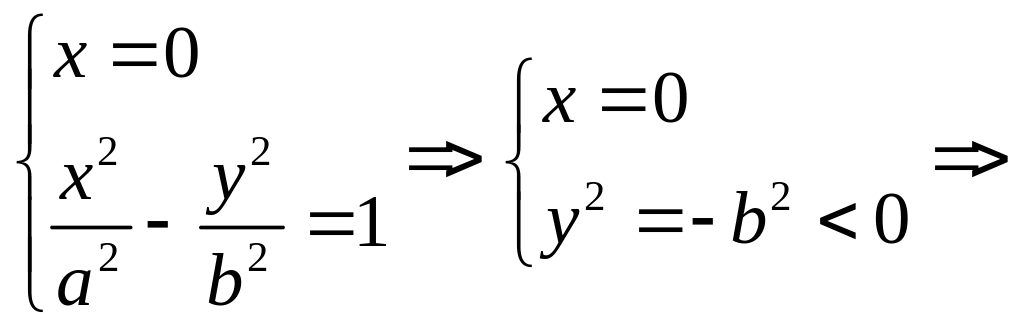точек пересечения с осью Oy нет.

Определение 2. Точки пересечения гиперболы с её фокальной осью называются вершинами гиперболы; фокальная ось называется также действительной осью. Ось, с которой гипербола не пересекается называется мнимой осью. Числа a>0 и b>0 называются соответственно действительной и мнимой полуосями.

3. Расположение относительно осей

Исследуем гиперболу в первом квадрате (четверти) то есть при и

;

b²x²-a²y² = a²b²;

y = .

Если 0 < a, то и принимает мнимые значения (точек гиперболы нет).

Если а, то при возрастании возрастает и , начиная от нуля при . Дуги гиперболы в остальных квадрантах симметричны этой дуге относительно осей координат и начала координат.

Гипербола состоит из двух изолированных ветвей.

Замечание. Так как , то и директрисы не пересекают гиперболу.

4. Асимптоты ( от греческого – несовпадающий, не касающийся)

Термин «асимптота» применительно к гиперболе приписывают Аполлонию Пергскому (III век до н.э.).

Рассмотрим прямую линию с уравнением , x > 0 и обозначим соответственно через M и N точки гиперболы и этой прямой, ….. общую абсциссу . Ординыты… этих точек обозначим через и , тогда имеем M(x;y_m), N(x;y_n­). Пусть для определённости эти точки находятся в первом квадрате.

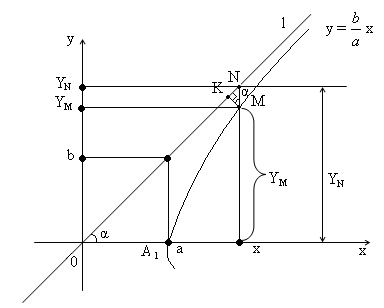
tg α = .

Пусть MK , тогда MK – расстояние от точки M гиперболы до прямой . Из MNK имеем MK = MN cos α, так как NMK = α = KOA₁ (углы соответственно перпендикулярным сторонам). Тогда имеем Y_N = x, Y_M = , так как a x, то

x- >0 и Y_N > Y_M. Следовательно: NM = Y_N-Y_M = (x- ).

Устраним абсциссу к бесконечности и рассмотрим предел:

= .

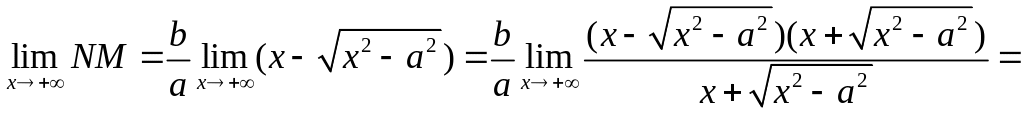
Но тогда и MK = MN cos α = cos α (x- ) при стремится к нулю.

Таким образом, точка М при неограниченно приближается к прямой . Если же , то к прямой неограниченно приближается и другая ветвь гиперболы в третьем квадранте.

Так как гипербола симметрична относительно оси Oy, то этими же свойствами обладает и прямая с уравнением .

Определение 3. Две прямые, к которым гипербола неограниченно приближается, нигде их не пересекая, называются асимптотами гиперболы.

OA₁ = a, A₁C₁ = b, . OC₁ = OF₁ = C, где с² = a² + b² = OC₁² = OF₁².

Другие виды уравнения гиперболы

1) Пусть гипербола задана уравнением:

. (3)

Тогда фокальной осью является ось Oy, и вершины гиперболы лежат на этой оси. Центр – О(0;0).

2) Пусть центр гиперболы находится в точке . Тогда если её оси параллельны осям то .

B₁(0;b), B₂(0;-b), F₁(0;c), ­F₂(0;-c). (c>b)

- директрисы; - асимптоты.

Определение 4. Гиперболы с уравнениями (1) и (3) называются сопряжёнными друг другу.

3) Сопряжённые гиперболы (1) и (3) имеют общие асимптоты с уравнениями .

4) Если a = b, то гипербола называется равносторонней. Уравнение (1) в этом случае имеет вид:

x² – y² = a² (4)

Асимптоты равносторонней гиперболы имеют уравнения и . Из формулы (2) получаем:

с² = 2а² .

В этом случае асимптоты равносторонней гиперболы содержат биссектрисы координатных углов и поэтому взаимно перпендикулярны.

Если эти асимптоты принять за оси прямоугольной декартовой системы координат, то в этой системе равносторонняя гипербола имеет уравнение:

или , (5)

где или .

Уравнение (5) называется уравнением гиперболы, отнесённой к свои асимптотам.

Таким образом, равносторонняя гипербола является графиком обратной пропорциональности.

5) Пусть центр гиперболы находится в точке . Тогда если её оси параллельны осям координат Ох и Оy, то имеем соответственно уравнения:

и .

Пример. Построим гиперболу с уравнением x² – 4y² = 4x.

Выделим полный квадрат с переменной :

(x² – 4x +4) – 4y² – 4 = 0, (x-2)² – 4y² = 4;

O^’(2;0), a = 2, b = 1, ;

OF₁ = OC₁ = .