§ 30. Способы задания прямой в пространстве

10. Параметрические уравнения прямой

Пусть прямая определяется в пространстве своей точкой и направляющим вектором .

Пусть также - произвольная точка прямой , где - текущие координаты, значит

|| , тогда существует число t такое, что:

, где .

Так как по правилу треугольника , то получаем:

- векторное уравнение прямой .

Поскольку ,

, то

(1)

(1) – параметрические уравнения прямой с параметром t, где .

20. Канонические уравнения прямой

Исключим параметр t из уравнений (1):

. (2)

(2) – канонические уравнения прямой (простейшие).

Замечания.

1) В уравнениях (1) и (2) числа x₀, y₀, z₀ – координаты фиксированной точки прямой.

2) Если в уравнениях (2) какие-либо два знаменателя равны нулю (две координаты какого-либо направляющего вектора прямой), то считаются равными нулю и соответствующие числители.

Пример 1. Составим канонические и параметрические уравнения оси OY:

или - канонические,

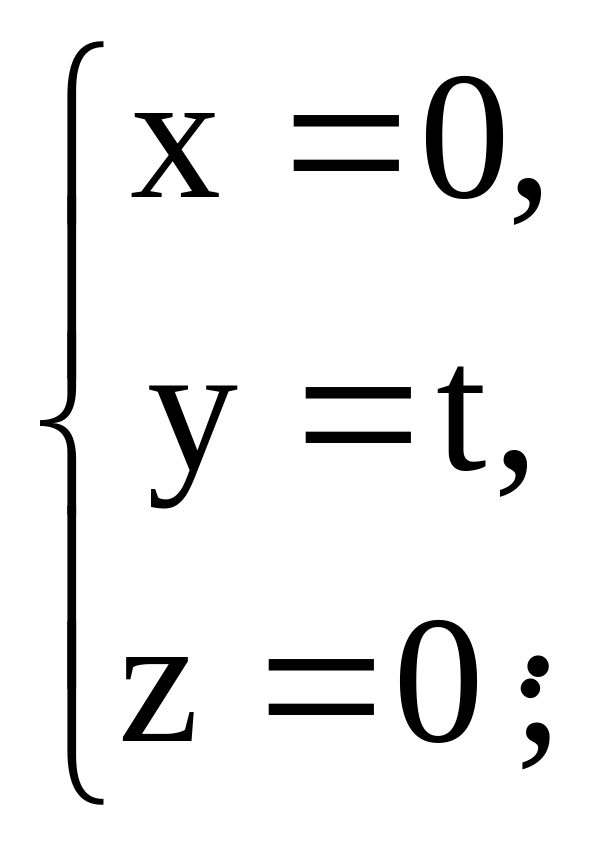
или – параметрические.

30. Связка прямых

Определение. Множество всех прямых пространства, проходящих через данную точку M₀, называется связкой прямых с центром в этой точке.

Множество всех прямых пространства, параллельных данной прямой, называется связкой параллельных прямых.

Замечания.

3) Пучок прямых отличается от связки прямых лишь тем, что состоит из прямых, лежащих в одной плоскости.

4) Если в уравнениях (2) изменять лишь знаменатели m, n, p, оставив постоянными x₀,y₀,z₀, то будут получаться уравнения различных прямых связки с центром M₀( x₀; y₀; z₀). Если же изменять x₀, y_0, z_0, оставив без изменения m, n, p, то будут получаться уравнения прямых некоторой связки параллельных прямых.

40. Уравнения прямой, проходящей через две точки

Пусть прямая задана двумя различными точками M₁( x₁; y₁; z₁) и M₂( x₂; y₂; z₂). В уравнениях (2) – канонических – примем за фиксированную точку M₁, а за направляющий вектор - .

Получаем искомые уравнения прямой:

. (3)

50. Общие уравнения прямой

Прямая как линия пересечения двух плоскостей определяется совместным заданием двух линейных уравнений:

(4)

при условии, что коэффициенты первого уравнения не пропорциональны коэффициентам второго уравнения (в противном случае эти уравнения будут определять параллельные или совпавшие плоскости).

Уравнения (4) называются общими уравнениями прямой.

Пример 2. Ось ординат Oy задается пересечением координатных плоскостей Oxy и Oyz, поэтому ее общие уравнения записываются так:

.

Способ перехода от общих уравнений прямой к каноническим.

1. Находим координаты направляющего вектора прямой :

и , поэтому || (отличается от числовым множителем). Можно, в частности, положить, = , где - векторное произведение векторов и .

2. Находим координаты какой-либо фиксированной точки M₀ прямой : одну из ее координат, например z₀, выбираем произвольно, подставляем ее в систему уравнений (4) и находим из нее остальные координаты x₀ и y₀.

Пример 3. Перейти от общих уравнений прямых к ее каноническим уравнениям:

l :

Решение.

1. Находим :

2. Находим точку M₀:

=> => => M₀(1;-1;0).

3. Находим канонические уравнения прямой.

или .

Легко видеть, что прямая может быть задана и другими общими уравнениями:

=>