§28. Группа симметрий фигуры.

Пусть - множество всех движений плоскости, переводящих фигуру F в себя. Очевидно, если движения f и g принадлежат множеству , то их композиция и движение g ° f и движение f^-1: также принадлежат множеству : g ° f и f^-1 . Следовательно, множество есть группа , которая является подгруппой группы D всех движений плоскости.

Определение 1: Если группа содержит элементы, отличные от тождественного преобразования е плоскости, то она называется группой симметрий фигуры F, а ее элементы – симметриями фигуры F. Если состоит из одного тождественного преобразования е, то говорят, что фигура F не имеет симметрий.

Примеры:

1. Г руппа симметрий правильного ∆АВС с центром О состоит из шести элементов (преобразований): трех поворотов е= , , и трех осевых симметрий : =

2. Г руппа симметрий равнобедренного треугольника ∆АВС состоит из двух элементов (преобразований): = , тождественного преобразования е и осевой симметрии . p⊥AB, AD=DB.

3. Группа симметрий разностороннего треугольника ∆АВС состоит из одного элемента – тождественного преобразования е. = , поэтому произвольный треугольник не имеет симметрий.

4. Г руппа симметрий окружности с центром О радиуса r состоит из бесконечного числа элементов. Любое вращение с центром О и любое отражение от прямой, проходящей через точку О является симметрией окружности .

Определение 2: прямая d называется осью симметрии фигуры F, если f , где f – отражение от прямой d. Точка М₀ называется центром симметрии фигуры F, если отражение от точки М₀ принадлежит группе .

(здесь отражение от прямой – осевая симметрия относительно этой прямой; отражение от точки – центральная симметрия относительно этой точки).

Примеры:

5. П араллелограмм, отличный от прямоугольника или ромба, имеет один центр симметрии – центр параллелограмма – м не имеет осей симметрии;

6. Прямоугольник или ромб, отличные от квадрата, имеют один центр симметрии и две оси симметрии d₁ и d₂ – прямые, на которых лежат диагонали ромба или серединные перпендикуляры к сторонам прямоугольника;

7. Квадрат имеет один центр симметрии и четыре оси симметрии – прямые d₁, d₂, АВ, ВD.

8. С уществуют фигуры, имеющие бесконечное множество центров и осей симметрии. Пусть F – точка между параллельными прямыми d₁ и d₂, а d₀ – прямая, параллельная d₁ и d₂ и отстоящая от них на равном расстоянии.

Тогда любая точка М₀ прямой d₀ является центром симметрии фигуры F, а любая прямая l⊥d₀, является осью симметрии этой фигуры.

§29. Группа преобразований подобия.

Определение 1: преобразованием подобия или просто подобием плоскости называется ее преобразование, при котором все расстояния между точками умножаются на одно и то же положительное число. Это число К называется коэффициентом подобия.

Замечание 1: если f – подобие плоскости, то по определению имеем:

.

Примеры:

1. Движение является подобием с коэффициентом К=1;

2. Гомотетией с центром С и коэффициентом Л называется преобразование плоскости, которое произвольную точку М плоскости отображает на такую точку М^/, что:

.

Обозначение: .

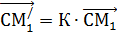3. Пусть М₁ и М₂ – произвольные точки плоскости , а и - их образы при гомотетии. Тогда , и . Таким образом, гомотетия добием с коэффициентом .

Теорема 1: множество подобий плоскости является группой относительно композиции. (Доказательство аналогично теореме движения).

Определение 2: фигура F называется подобной фигуре F^/, если существует подобие плоскости, отображающее фигуру F на фигуру F^/.

Обозначение: F F^/.

Теорема 2: подобие фигур является отношением эквивалентности. (Доказательство аналогично доказательству соответствующей теоремы для отношения равенства фигур).

Определение 3: подобие, не меняющее ориентацию плоскости, называется подобием 1-го рода. Подобие, изменяющее ориентацию плоскости на противоположную, называется подобием 2-го рода.

Замечание 2: подобия 1-го рода образуют группу; подобия 2-го рода группу не образуют.

Таким образом, имеет место следующая классификация:

Замечание 3: Из курса геометрии средней школы известно, что преобразование подобия обладает свойствами:

1. Сохраняют отношение «лежать между» для точек;

2. Отображают отрезок на отрезок, луч – на луч, прямую – на прямую, угол – на угол, многоугольник – на многоугольник;

3. Сохраняют величины (меры) углов;

4. Сохраняют отношение, в котором точка делит отрезок (в частности, середину отрезка отображают на середину образа этого отрезка).

5. Можно доказать, что гомотетия сохраняет ориентацию плоскости.