§18. Парабола (“приложение”)

Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки F, называемой фокусом, и данной прямой l, не проходящей через фокус, называемой директрисой.

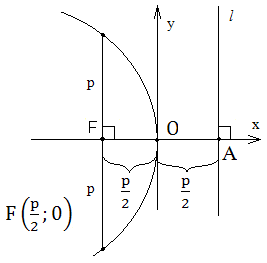
Для вывода уравнения параболы за ось Ox примем прямую, проходящую через фокус F перпендикулярно директрисе l. За положительное направление оси абсцисс возьмём направление от директрисы к фокусу. За начало координат возьмем точку O, которая делит пополам отрезок от директрисы до фокуса. Длину этого отрезка обозначим через P и назовем фокальным параметром параболы.

Тогда фокус F имеет координаты , а точка A оси Ox, через которую проходит директриса l, имеет координаты . Возьмем произвольную точку M(x,y) параболы и соединим ее с фокусом F, а затем опустим перпендикуляр MN на директрису l. При этом длину отрезка MN обозначим через r и назовем фокальным радиусом точки M, а длину отрезка MN обозначим d. Тогда по определению параболы имеем: .

Замечание: По аналогии с эллипсом и гиперболой число , назовем директрисой параболы. Так как r=d, то для параболы .

Теорема. Пусть прямоугольная декартова система координат Oxy выбрана указанным выше способом. Тогда в этой системе координат парабола имеет каноническое уравнение: .

Доказательство.

Пусть M(x;y) – произвольная точка параболы, – фокус, или – уравнение директрисы. Тогда имеем:

; - расстояние от точки M(x,y) до прямой l, причем x≥0.

.

.

Теорема доказана.

§19. Исследование уравнения параболы

Пусть парабола задана каноническим уравнением:

(1)

1. Ось и вершина

Так как уравнение (1) содержит переменную во второй степени, то оно не изменится при замене на , следовательно, парабола симметрична относительно оси абсцисс Ox.

Других осей симметрии и центра симметрии у параболы нет.

С осью Ox парабола пересекается в начале координат, так как при имеем и .

Определение. Ось симметрии параболы называется ее осью, точка пересечения параболы с осью называется ее вершиной.

2. Расположение относительно оси и директрисы

Так как (расстояние), то из (1) имеем: . Следовательно, парабола расположена относительно оси Oy, а следовательно, и относительно и директрисы по ту же сторону, что и фокус. Если , то . Следовательно, при неограниченном удалении от вершины парабола неограниченно удаляется от оси.

3. Фокальная хорда

Определение. Фокальной называется хорда, проходящая через фокус параболы перпендикулярно ее оси.

Покажем, что ее длина равна удвоенному фокальному параметру:

4. Другие виды уравнения параболы

1) .

2) .

3) .

4) .

5) .

Oˡ(x₀;y₀) – вершина параболы.

§20. Уравнения эллипса, гиперболы и параболы в полярных координатах

Теорема 1. Эллипс, отличный от окружности, гипербола и парабола являются множествами точек плоскости, для которых отношение расстояния до данной точки F к расстоянию до данной прямой l есть величина постоянная.

Замечания.

1) Для эллипса и гиперболы теорема 1 непосредственно следует из теоремы о директрисах, причем F – один из фокусов, l – ближайшая к этому фокусу директриса. Для параболы теорема 1 следует из ее определения, где F – фокус параболы, l – ее директриса;

2) Указанное отношение расстояний есть эксцентриситет линии;

3) Окружность не имеет директрис, так как Ɛ=0 и .

Теорема 2. Эллипс, гипербола, парабола, эксцентриситетами Ɛ имеют в некоторой полярной системе координат уравнение:

. (1)

Доказательство.

Примем за полюс фокус F соответствующей линии, полярную ось проведем через фокус F перпендикулярно соответствующей директрисе l в направлении от l к F.

Пусть M – произвольная точка линии, M₀ – точка линии, для которой ; обозначим FM₀ через p – фокальный параметр точки M₀.

;

Согласно теореме 1 имеем:

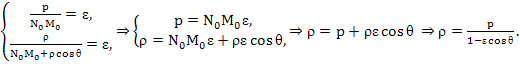
Замечания.

1) Для параболы Ɛ=1, p – фокальный параметр, тогда парабола имеет полярное уравнение .

2) Для эллипса и гиперболы - уравнениям

и (2)

, (3)

получаем: .

Например, для уравнения (2) имеем: =p – фокальный параметр, тогда для точки M₀ эллипса имеем:

.

Для окружности Ɛ=0 и ее полярное уравнение принимает вид: , где p – радиус окружности, .