§30. Формулы подобия.

Пусть имеется некоторая гомотетия плоскости. Выберем на плоскости прямоугольную декартову систему координат , обозначим через (х;у) координаты произвольной точки М, а через (х^/;у^/) – координаты ее образа М^/ при гомотетии в этой же системе координат:

.

Найдем аналитическое выражение гомотетии коэффициенты К задается формулами:

… (1)

Доказательство.

Пусть М , тогда по определению гомотетии имеем:

.

, тогда получаем:

⇒ ⇒ (1)

Теорема доказана.

Следствие: гомотетия с центром в начале координат с коэффициентом К задается формулами:

(2)

Теорема 2: пусть f – подобие с коэффициентом К, а h – гомотетия с тем же коэффициентом К и центром в произвольной точке М₀. Тогда существует одно и только одно движение такое, что:

(3)

Доказательство.

1. Существование движения .

Рассмотрим преобразование плоскости

(4)

Оно является преобразование подобия с коэффициентом , то есть движением из равенства (4) имеем:

.

Таким образом, существует движение , удовлетворяющее условию (3).

2. Единственность движения .

Пусть теперь –произвольное движение плоскости, такое, что . Учитывая равенство (4), приходим к выводу, что = .

Теорема доказана.

Теорема 3: в прямоугольной декартовой системе координат подобие с коэффициентом К задается формулами:

(5)

где в случае подобия 1-го рода,

в случае подобия 2-го рода.

Доказательство.

Пусть f – подобие с коэффициентом К. тогда по теореме 2 имеем: , где h – гомотетия с центром в начале координат О (0;0) и коэффициентом К, а - некоторое движение.

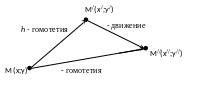
Запишем в системе координат формулы преобразований h и :

,

Тогда получаем формулы композиции

или, обозначив координаты точки М(х;y), а ее образа при композиции - подобие с коэффициентом К – через х^/ и у^/, приходим к формулам (5). Теорема доказана.

Теорема 4: любое преобразование подобия, отличная от движения, имеет одну и только одну неподвижную точку.

Следствие: любое преобразование подобия, имеющее более одной неподвижной точки или не имеющее ни одной неподвижной точки, является движением.

Замечания:

1. Используя теорему 4 и следствие из нее, можно провести классификацию преобразований подобии в зависимости от наличия неподвижных точек и инвариантных прямых. При этом прямая называется инвариантной при преобразовании плоскости f, если ее образ при f совпадает с ней;

2. Имеет место обратная теореме 3.

Теорема 5: любое преобразование, задаваемое в прямоугольной декартовой системе координат формулами (5), является преобразованием подобия.

§31. Группа аффинных преобразований.

Определение 1: преобразование плоскости называется аффинным, если оно обладает следующими свойствами:

1. Любую прямую отображает на прямую;

2. С охраняет отношение, в котором точка делит отрезок.

, , ⇒λ=λ^/.

Замечания:

1. Аффинное преобразование можно определить и как преобразование, отображающее прямую на прямую. При этом второе свойство может быть доказано в качестве теоремы, однако это доказательство довольно сложное;

2. Из второго свойства следует, что аффинное преобразование сохраняет отношение «лежать между», и, значит, отображает отрезок на отрезок, луч на луч, аффинную систему координат на аффинную систему координат.

Определение 2: аффинное преобразование называется перспективно-аффинным или родственным, если оно имеет прямую неподвижных (двойных) точек – ось родства.

Аффинное преобразование называется аффинным преобразованием 1-го рода, если оно сохраняет ориентацию плоскости, и аффинным преобразованием 2-го рода, если изменяет ее на противоположную.

Пример 1: любое подобие, в частности движение, является аффинным преобразованием. Осевая симметрия дает пример родственного преобразования плоскости.

Замечание 3: перспективно- аффинное преобразование плоскости обладает следующими свойствами:

1°. Любая точка прямой, проходящей через две неподвижные точки родственного преобразования, является неподвижной точкой;

2°. Прямые, соединяющие соответственные точки родственного преобразования, не лежащие на его оси, параллельны или совпадают.

(f: M M^/, N N^/)⇒(MM^/║NN^/).

3°. Если прямая пересекает ось родства в некоторой точка, то ее образ проходит через эту точку; если же прямая параллельна оси родства, то ее образ также параллелен оси родства.

f: l l^/⇒ l l^/=L₀ p;

f: m║p, m m^/⇒ m^/║p.

следует заметить, что в отличии от осевой симметрии, отрезки, соединяющие соответственные точки родственного преобразования плоскости, не обязательно перпендикулярны оси родства и могут не делится этой осью пополам:

М М^/ р, ММ₀ М₀М^/ (см. рис. 1).

Примет 2: даны ось родства, точка А, не лежащая на оси р, и ее образ А^/. построим образ М^/ произвольной точки М.

Р ешение.

1. П усть АМ∦р и М АА^/.

1. Строим точку А₀=АМ∩р;

2. Строим прямую m:

M m, m║AA^/;

3. Строим точку М^/=m∩А₀А^/.

2. Пусть АМ║р и М^/=АА^/∩l^/, где l^/=f(АМ)║р и А^/ l^/.

3. П усть М АА^/. В этом случае следует взять вспомогательную точку N AA^/, построить ее образ N^/, и затем, пользуясь точками N и N^/, вышеуказанным способом построить образ точки М.

П остроение:

1. N AA^/;

2. ∩p=A₀;

3. A₀A^/;

4. l║AA^/, N l;

5. N^/=l∩A₀A^/ - образ точки N;

6. B₀=MN;

7. M^/=B₀N^/∩AA^/ - образ точки М.

Таким образом, родственное преобразование плоскости задается осью родства и парой соответствующих (родственных) точек.

Теорема 1: множество всех аффинных преобразований плоскости является группой относительно композиции.

Доказательство.

1. Пусть f₁ и f₂ – произвольное аффинное (не обязательно родственное) преобразования плоскости. Они отображают прямую на прямую и сохраняют отношение, в котором точка делит отрезок. Но тогда и их композиция f= f₂°f₁ обладает теми же свойствами, то есть также является аффинным преобразованием.

2. Преобразование f^-1 отображает прямую на прямую и сохраняет отношение, в котором точка делит отрезок, то есть является аффинным преобразованием.

Согласно определению группы преобразований множество всех аффинных преобразования плоскости является группой относительно композиции.

Теорема доказана.

Пример 3: подгруппами группы всех аффинных преобразований плоскости являются:

1. Группа подобий и все ее подгруппы;

2. Группа всех аффинных преобразований 1-го рода;

3. Группа, состоящая из двух преобразований родства с данной осью и тождественного преобразования плоскости.

Определение 3: фигура F называется аффинно-эквивалентной фигуре F^/, если существует аффинное преобразование плоскости f, отображающее фигуры F на фигуру F^/.

Замечания:

4. Аффинная эквивалентность фигур является отношением эквивалентности. Это доказывается также, как и для равенства или подобия фигур:

5. М ожно доказать, что любые два треугольника аффинно-эквивалентны, при этом существует одно и только одно аффинное преобразование, отображающее один треугольник на другой. То есть задание двух соответственных треугольников определяет аффинное преобразование плоскости. Аналогично, задание любых двух соответственных аффинных систем координат вполне определяет аффинное преобразование плоскости.

Теорема 2: аффинное преобразование сохраняет параллельность прямых.

Дано: a║b.

Доказать: a^/║b^/, где а^/=f(a), b^/=f(b), f – произвольное аффинное преобразование.

Доказательство.

Предположим противное, то есть, что a^/∩b^/=M^/ - прямые a^/ и b^/ пересекаются в некоторой точке M^/. Тогда, если М – прообраз М^/ при аффинном преобразовании f, то должно быть a∩b=M. Получаем противоречие с условием (a║b) и доказываем теорему.

Следствие 1: любые два параллелограмма аффинно-эквивалентны.

С ледствие 2: аффинное преобразование сохраняет отношение длин параллельных отрезков:

, где =f(ABCDE).

Замечание 6: если длина отрезков, величины углов, отношения длин параллельных отрезков могут измениться. Например, образом данного квадрата может оказаться произвольный параллелограмм, но не может быть трапецией.

F

F^/

f

Теорема 3: в аффинной системе координат О_ху аффинное преобразование плоскости f выражается формулами.

(*)

Где и .

Доказательство аналогично доказательству соответствующей теоремы для движений, только здесь используется формулы перехода от одной аффинной системы координат.

Замечания:

7. В формулах (*) свободные члены х₀ и у₀ есть координаты точки О^/ - образа начала координат О при аффинном преобразовании f, то есть f(0) = O^/( х₀;у₀); числа a₁, a₂ и b₁, b₂ – координаты соответственно векторов и в базисе ( ; ), то есть а₁ +а₂ , b₁ +b₂ ;

8. Если f – аффинное преобразование 1-го рода, то , если второго 2-го рода, то ;

9. Имеет место теорема, обратная теореме 3.

Теорема 4: если преобразование f плоскости в некоторой аффинной системе координат задано формулами (*), то f – аффинное преобразование. В случае ( ) оно аффинным преобразованием 1-го рода (2-го) рода.