§26. Группа движений.

Определение 1: движением или перемещением плоскости называется ее преобразование, сохраняющие расстояние между точками.

Замечание 1: если f – движение плоскости, то по определению:

(М M^/⋏N N^/)⇒(MN=M^/N^/).

Пример 1: тождественное преобразование, поворот, параллельный перенос, осевая и центральная симметрии есть движения.

Теорема 1: множество всех движений плоскости является группой.

Доказательство.

1. П 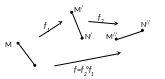усть f₁ и f₂ – два любых движения плоскости. По определению 1 каждое из них сохраняет расстояние между точками, то тогда их композиция f= f₁°f₂ также сохраняется расстояние между точками, то есть является движением.

N

(MN=M^/N^/⋏M^/N^/=M^//N^//) ⇒ (MN= M^//N^//).

2. Пусть f – любое движение плоскости. Оно сохраняет расстояние между точками, то тогда расстояние не будет изменятся и при обратном преобразовании f^-1. Следовательно, преобразование f^-1 есть движение.

(MN=M^/N^/)⇒ (M^/N^/=MN).

Согласно определению 2 из §25 множество движений плоскости является группой.

Определение 2: фигуры F называется равной фигуре F^/, если существует движение f, отображающее F на F^/: F^/=f(F).

Обозначения: F=F^/.

Теорема 2: равенство фигур является отношением эквивалентности, то есть обладает свойствами рефликсивности, симметричности и транзитивности.

Доказательство.

1. При тождественности преобразования ε любая точка фигуры F отображается на себя:

F F.

Так как тождественное преобразование является движением, то любая фигура F равна самой себе:

F=F – рефлексивность.

2. Пусть F=F^/. Это значит, что существует движение f, отображающее F на F^/:

F F^/.

Но так как f – движение, то существует ему обратное движение f^-1, отображающие F^/ на F:

F^/ F

Согласно определению 2 имеем F=F^/. Таким образом:

(F=F^/)⇒(F^/=F) – симметричность.

3. Пусть F=F^/ и F^/=F^//. Это значит, что существует такие движения f₁ и f₂, что:

F F^/ и F^/ F^//.

Но композиция f=f₂°f₁ отображают F на F^///

Так как по теореме 1 f=f₂°f₁ – движение, то по определению 2 имеем: F=F^//.

Таким образом:

(F=F^/⋏F^/=F^//)⇒(F=F^//) – транзитивность.

Замечание 2: из курса геометрии средней школы известно, что движения обладают следующими свойствами:

1. Сохраняют отношение «лежать между» для точек;

2. Отображают отрезок на отрезок, луч – на луч, прямую – на прямую, угол – на угол, многоугольник – на многоугольник;

3. Сохраняется величина (меры) углов;

4. Отображают прямоугольную декартову систему координат на прямоугольную декартову систему координат.

Определение 3: движение 1-го рода называется движение, сохраняющее ориентацию плоскости, то есть отображающее правую систему координат на правую, левую – на левую. Если движение изменяет ориентацию плоскости, то есть изменяет тип системы координат, то оно называется движением 2-го рода.

П ример 2: - движение 1-го рода:

ПРАВАЯ O^/x^/y^/= ( )

ПРАВАЯ = .

П ример 3: - движение 2-го рода:

О^/х^/у^/= (О_ху)

Замечание 3: Множество движений 1-го рода является группой, а движений 2-го рода – не является группой, так как композиция двух движений 2-го рода дважды меняет ориентацию плоскости на противоположную и вследствие этого является движением 1-го рода по определению (см. определение 3).

Определение 4: скользящей симметрией называется преобразование плоскости, является композицией осевой симметрии и параллельного переноса в направлении оси симметрии.

F= ° = ° ,

Где p, так как

М^//=( ° )(М)=( ° )(М).

Замечание 4: скользящая симметрия является движением 2-го рода, так как изменяет на противоположную ориентацию плоскости.

Имеет место основная теорема о структуре группы движений плоскости.

Теорема 3 (Мишеля Шаля (1798-1880) – французский геометр, создал новое направление в математике – вычислительную геометрию): всякое движение плоскости является одним из следующих преобразований:

1. Поворот (включая центральную симметрию и тождественное преобразование);

2. Параллельный перенос;

3. Осевая симметрия;

4. Композиция поворота и параллельного переноса;

5. Скользящая симметрия.

Следствие: всякое движение плоскости является композицией следующих движений:

1. Поворот;

2. Параллельный перенос;

3. Осевая симметрия.