§35. Однополостный гиперболоид

Однополостный гиперболоид задается своим каноническим уравнением:

. (1)

1. Плоскости, оси и центр симметрии

Как и в случае эллипсоида доказывается, что однополостный гиперболоид с уравнением (1) симметричен относительно всех координатных плоскостей, всех осей координат и начала координат.

Таким образом, оси координат служат осями однополостного гиперболоида, а начало координат – его центром.

2. Вершина

Ox:

Oy:

Oz: точек пересечения нет.

Определение. Действительными осями однополостного гиперболоида называются те оси, с которыми он пересекается. Третья ось, с которой он не пересекается, называется мнимой осью. Числа a, b, c называются полуосями однополостного гиперболоида.

3. Главные сечения

Сечение плоскостью Oyz: - гипербола с мнимой осью Oz (вершина на оси Oy).

Сечение плоскостью Oxz: - гипербола с мнимой осью Oz (вершина на оси Ox).

Сечение плоскостью Oxy: - эллипс с полуосями a и b.

4. Сечение плоскостью, параллельной плоскости Oxy

αǁOxy: или . (2)

Уравнения (2) определяют эллипс с полуосями при любом . Если h=0, то полуоси принимают наименьшие значения: a₁=a, b₁=b. Полученное главное сечение называется горловым эллипсом.

Если , то полуоси a₁, b₁ неограниченно возрастают.

5. Сечение плоскостью, параллельной плоскости Oyz

βǁOxy: (3)

Возможны три случая:

1. Уравнения (3) определяют гиперболу с мнимой осью, параллельной оси Oz:

и полуосями , .

2. Уравнения (3) определяют пару прямых, пересекающихся в точках (±a;0;0):

.

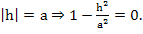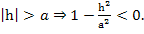3. Уравнения (3) определяют гиперболу с мнимой осью, параллельной оси Oy:

и полуосями , .

Аналогичный результат получается и при пересечении поверхности с уравнением (1) плоскости γ с уравнением y = h, где γ ║ Oxz.

Изобразим теперь однополостный гиперболоид, используя проведенное выше исследование его формы.

6. Виды однополостных гиперболоидов

а) Если a = b, например, то уравнение (1) задает поверхность вращения, а именно однополостный гиперболоид вращения.

(4)

Эта поверхность получается вращением гиперболы с уравнениями вокруг оси Oz, то есть вокруг мнимой оси гиперболы.

б) Однополостный гиперболоид с центром O’(x₀,y₀,z₀) и полуосями a, b, c, параллельными осям координат, имеем уравнение:

(5)

Пример. Изобразить поверхность второго порядка в : .

Решение.

однополостный гиперболоид вращения, a = c = 1, b = 2; ось вращения – ось Oy.

§36. Двуполостный гиперболоид

Двуполостный гиперболоид задается своими каноническим уравнением

или (1)

1. Плоскости, оси и центр симметрии

Из уравнения (1) следует, что поверхность симметрична относительно всех плоскостей координат, всех координатных осей и начала координат. Таким образом, двуполостный гиперболоид имеет три оси и один центр – начало координат.

2. Вершины

Точки пересечения с осью Oz: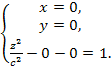 , C₁(0, 0, c), C₂(0, 0, -c).

Легко видеть, что точек пересечения с другими осями координат нет:

Ось Ox: .

Ось Oy: .

Определение. Действительной осью двуполостного гиперболоида называется та ось, с которой он пересекается. Две другие оси называется мнимыми (с ними двуполостный гиперболоид не пересекается).

3. Главные сечения

. (1)

Сечение плоскостью OYZ: гипербола с действительной осью OZ.

Сечение плоскостью OXZ: гипербола с действительной осью OZ.

Сечение плоскостью OXY: пустое множество точек (мнимый эллипс).

4. Сечение плоскостью, параллельной плоскости OXY

║OXY: или (2)

Возможны три случая.

а) и плоскость α двуполостный гиперболоид не пересекает, так как система (2) не имеет решений.

б) и имеет систему

сечением является либо точка C₁(0, 0, c), либо C₂(0, 0, -c), то есть одна из вершин двуполостного гиперболоида.

в) и имеет систему

(3)

Второе уравнение системы (3) задает эллипс , где .

Если , то полуоси этого эллипса и неограниченно возрастают.

Аналогично можно показать, что сечениями поверхности с уравнением (1) плоскостями β: x = h и γ: y = h есть гиперболы.

Изобразим теперь двуполостный гиперболоид, используя проведенное выше исследование его формы.

5. Виды двуполостных гиперболоидов

а) Если в уравнении (1), например a = b, то получаем двуполостный гиперболоид вращения с уравнением:

(4)

в котором ось вращения – ось Oz

Эта поверхность получена вращением гиперболы с уравнением вокруг оси Oz, то есть вокруг ее действительной оси.

б) Двуполостный гиперболоид с центром и полуосями a, b, с, параллельными осям координат, имеем уравнение:

(5)

Замечание. В каноническом уравнении однополостного гиперболоида имеется один знак «-», а в каноническом уравнении двуполостного гиперболоида – два знака «-».

В обоих уравнениях члены, соответствующие действительным осям, имеют знак «+», а члены, соответствующие мнимым осям, имеют знак «-».

Пример. Изобразить поверхность второго порядка .

Решение.

.

- двуполостный гиперболоид вращения, центр , полуоси a = b = с = 1.

(Формула параллельного переноса в пространстве имеет вид.

, где