IV Преобразование плоскости

§21. Понятие отображения.

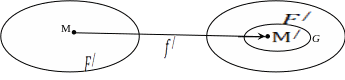
Определение 1: пусть имеются две фигуры F и G – множество точек, причем произвольной точке М фигуры F соответствует определенная точка фигуры G. Тогда:

1. это соответствие называется отображением фигуры F в фигуру G;

2. точка называются образом точки ;

3. точка называется прообразом точки ;

4. если точки и совпадают ( ), то точка М называется неподвижной или двойной точкой отображения;

5. фигура , состоящая из образов всех точек фигуры , называется образом фигуры F.

Обозначения:

F – отображение;

или

или .

пусть F=AB – гипотенузы прямоугольного , G=AC прямая соединяющая его катет АС, f – ортогональное проектирование на прямую АС.

Имеем

C – образ В: f(В)=С, В^/ C;

М^/ -образ М: f(М)=М^/, где М АВ=F;

А – неподвижная очка преобразования f: f(А)=А^/, А=А^/.

Точка D АС не имеет прообраза в фигуре F F^/ G.

F G – F^/ является подмножеством множества точек G.

Катет АС – образ гипотенузы АВ=F:

f(F)=АС=F^/.

Замечание 1: по определению каждая точка М фигуры F при отображении f в фигуру G имеем один образ М^/. Число же прообразов для М для точки М^/ фигуры G может быть различным (большим или равным одного).

Определение 2: если каждая точка фигуры G имеем хотя бы одон прообраз в фигуре F, то отображение f: F G называется сюръекцией и в этом случае говорят об отображении фигуры G/

F на G (сюръекция).

f(А)=А^/ - точка А^/ имеет один прообраз в F.

f(В)=В^/ - точка В^/ имеет два прообраза в F.

З

амечание 2: отображение является сюръекцией тогда и только тогда, когда - G является образом F.

Определение 3: если для любых двух различных точек М₁ М₂ фигуры F f(М₁) f(М₂), то отображение f фигуры F в фигуру G называется инъекцией.

Определение 4: если отображение одновременно является сюръекцией и инъекцией, то оно называется взаимно однозначным отображением фигуры F на фигуру G или биекцией.

А^/= f(А), В^/= f(В), С^/= f(С). Точки А^/, В^/, С^/ фигуры G имеют один и только один прообраз, f(А) f(В) f(С); f – биекция.

Замечание 3: биекция является частным случаем сюръекции (каждая точка фигуры G имеет единственный прообраз).

Определение 5: инвариантными отображениями называются свойства фигур, тела или функции, связанные с фигурами, которые сохраняются при этом отображении.

Пример 2: в примере 1 имеем (f – ортогональное проектирование).

1. длина отрезка не является инвариантом ортогонального проектирования f на каким АС точек гипотенузы АВ, так как АМ А^/М^/;

2. отношение (число) λ, в котором точка М делит отрезок АВ, является инвариантом отображения f, так как по теореме Фалеса;

3. свойство точки М «лежать между» точками А и В является инвариантом отображения f, так как при нем М^/также лежит между А^/ и В^/.

§22. Отображения фигур на плоскости.

Определение 1: формулы связывающие координаты x^/, y^/ образа М^/ произвольной точки М и ее координаты x, y относительно выбранной (аффинной или прямоугольной декартовой) системы координат Оxy, называются формулами или уравнениями соответствующего отображение.

Определение 2: отображения фигуры F называется тождественным, если все точки фигуры F являются тождественными (двойными).

Обозначение: ε; ε(F)=F; формулы: ε:

О пределение 3: параллельным переносом фигуры F называется ее отображение, при котором все ее точки смещаются на одно и тоже расстояние в одном направлении.

Е сли обозначить , то говорят о параллельном переносе на вектор α и пишут: F^/= (F) .

Выведем формулы параллельного переноса.

Пусть , М(x; y), М^/(x^/;y^/). Тогда - по определении 3 или в координатах

Определение 4: поворотом фигуры F вокруг центра С на направленный угол α называется ее отображение, при котором:

1. точка С является неподвижной;

2. л юбая точка М F отображается на такую точку М^/, что СМ=СМ^/ и .

Обозначение:

С

Определение 5: центральной симметрией с центром С называется поворотом вокруг центра С на угол α=π.

Обозначение: М^/=Z_C(M)= .

П

У

ример 1: пусть С=О (0;0), тогда имеем:

Определение 6: осевой симметрией c осью р называется отображение фигуры F, при котором ее любая точка М отображается на точку М^/, симметричную точке М относительно прямой р.

ММ^/ р, М₀=ММ^/∩р,

ММ₀=М₀М^/.

Р – прямая неподвижных точек

(например, точки М₀, N₀, K₀).

Обозначение: М^/=S_р(М).

Пример 2: р=О_х

S_ох:

у

Пример 3: р=О_у

S_ох: