VI. Плоскости и прямые
§ 1. Общее уравнение плоскости
1о
Определение 1. Нормалью к плоскости называется любая прямая, перпендикулярная этой плоскости. Нормальным вектором плоскости называется направляющий вектор её нормали.
Замечания.
Мы будем использовать прямоугольную декартову систему координат
Совпадающие плоскости или совпадающие прямые будем называть параллельными в широком смысле.
Теорема
1.
Плоскость, проходящая через точку Мo(xo;
yo;
zo)
и имеющая нормальный вектор 
,
определяется уравнением:
. (1)
Доказательство.
Пусть
– нормальный вектор данной плоскости
α, а M(x,
y,
z)
– произвольная точка плоскости α.
Тогда имеем (согласно определению перпендикулярности прямой и плоскости):
П
оэтому
,
откуда и следует равенство (1). Для любой
же точки N,
не принадлежащей α, соответственно
,
и равенство (1) не выполняется. Итак,
каждую плоскость можно задать линейным
уравнением с тремя переменными, имеющим
хотя бы один ненулевой коэффициент.
Теорема доказана.
Теорема 2.
Всякое уравнение первой степени вида:
ax + by + cz + d = 0, (2),
где хотя бы один из коэффициентов a, b, c отличен от нуля, является уравнением некоторой плоскости;
Обратно, уравнение любой плоскости может быть заменено в виде (2).
Доказательство.
1) Уравнение вида (2) имеет бесконечное множество решений, пусть (xo; yo; zo) – одно из таких решений, тогда выполняется равенство:
a xo + byo + czo + d = 0. (3).
Вычитая
из уравнения (2) уравнение (3), получим
уравнение (1), которое задаёт плоскость,
проходящую через точку Мo(xo;
yo;
zo)
и имеющую нормальный вектор 
.
Единственность такой плоскости
доказывается методом от противного.
2) Обратно, пусть плоскость задаётся уравнением
,
обозначив
получаем уравнение вида (2).
Теорема доказана.
Определение 2. Уравнение плоскости вида (2) называется её общим уравнением.
2о
Частные виды общего уравнения плоскости:
1)
В уравнении (2) отсутствует свободный
член:
,
.
Координаты точки О
(0; 0; 0)
удовлетворяют этому уравнению, плоскость
проходит через начало координат.
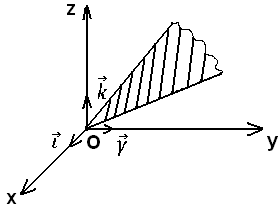
2)
В уравнении (2) отсутствует одна из
координат. Пусть, например, отсутствует
аппликата z,
то есть 
,
.
При
этом 
этот вектор компланарен векторам i
и j,
следовательно, 
.
Плоскость параллельна
оси Oz
(и
перпендикулярна плоскости Oxy).
При 
плоскость проходит через точку О,
и, следовательно, и через ось аппликат
Oz.
Аналогично,
– уравнение плоскости, параллельных
оси Ox
(перпендикулярной
плоскости Oyz).
При d=0
эта
плоскость проходит через ось абсцисс
Ox.
- уравнение плоскости, параллельной оси
Oy
(перпендикулярной
плоскости Oxz).
При d=0
эта
плоскость проходит через ось ординат
Oy.
Пример 1. 2x – z = 0.
a = 2, b = 0, c = -1, d = 0 => плоскость проходит через ось ординат Oy. Положим x = 1, y = 0, тогда z = 2, затем положим x = 1, y = 5, снова z = 2.
3)
В уравнении (2) отсутствуют две координаты.
Пусть, например, отсутствуют ордината
y
и аппликата z:
Плоскость параллельна оси Oy
и параллельна оси Oz,
следовательно, она параллельна плоскости
Oyz
(перпендикулярна оси абсцисс Ox).
Уравнение её можно записать в виде:
или 
Если
ао
= 0,
то получаем уравнение плоскости Oyz:
Аналогично:
или 
- уравнение плоскости, параллельной
плоскости Oxz
(и
⊥-ой
оси ординат плоскости Oy).
При
получаем уравнение плоскости Oxz:
или 
- уравнение плоскости, параллельной
плоскости Oxy
(и
перпендикулярной оси аппликат Oz).
При
получаем уравнение плоскости Oxy:
.
Пример 2. y+2z-4=0, a=0, b=1, c=2, d=-4, плоскость параллельна оси OX
Положим x=y=0 => z=2; X=z=0 =>y=4.
Уравнение координатных осей.
OX=Oxy
∩ Oxz
OY=Oxy
∩ Oyz
OZ=Oxy
∩ Oyz
