§23. Композиция отображений.

Определение: Композицией или произведением отображений f₁ и f₂ называется отображение f, являющиеся результатом последовательного выполнения системы отображения f₁, затем f₂.

О бозначение: f= f₂°f₁.

М^/=f₁(M); М^//=f₂(M);

М^//=f₂°(f₁(M))= (f₂°f₁)(M).

Примеры:

1. е – тождественное отображение, f – произвольное отображение, тогда имеем:

е °f=f°е;

2. f₁= , f₂= , тогда имеем:

° =

3. f₁=Z_C=f₂, тогда имеем:

Z_C°Z_C= ° = = =e =e.

4. f₁= 2₁=

Найдем формулы композиции f₂°f₁.

М ^/=f₁(M):

М^//=f₂(M^/):

М^//=f₂(f₁(M))= (f₂°f₁)(M): ⇒ f₂°f₁:

Координаты исходной точки фигуры обозначают через x и y, а ее образа – x^/, y^/. Поэтому удобнее следующая запись:

f₂°f₁: f₁°f₂:

Теорема: для композиции отображений справедлив ассоциативный (сочетательный) закон:

f₃°(f₂°f₁)= (f₃°f₂)°f₁ (1)

Доказательство.

П усть М – произвольная точка фигуры F и М M^/, М^/ M^//, М^// M^///.

М^//=f₂°f₁(M), М^///=f₃(M^//)⇒

М^///=f₃°(f₂°f₁)(M) (2)

М^/=f₁(M), М^///=(f₃° f₂)(M^/)⇒

М^///=(f₃°f₂)°f₁(M) (3)

Тогда имеем М М^//, М^// М^///, то есть с одной стороны М М^///, с другой стороны М М^/, М^/ М^///, то есть М М^///.

В следствии произвольного выбора точки М фигуры F из соотношений (2) и (3) следует формула (1).

Замечание: коммутативный закон для композиции отображений иногда справедлив, иногда – нет, то есть в общем случае: f₂°f₁ f₁°f₂.

Примеры:

1. ° =

° =

° = °

2. f₁=S_p, f₂=S_q, p q (p и q различны и p q)

M М^/ М^//

M М₁^/ М₁^//

М₁^// M^//⇒ S_q° S_p S_p° S_q.

§24.Обратное отображение.

О пределение 1:отображением, обратным отображению f фигуры F на фигуру F^/, такое отображение фигуры F^/ на фигуру F, при котором любая точка М^/ фигуры F^/ отображается на свой прообраз М фигуры F относительно отображения f.

Обозначение: f^-1

Замечания:

1. f(M)=M^/ f^-1(M)=M;

2. f^-1° f=f° f^-1=ε ⇒( f^-1)^-1=f;

3. отображение имеет себе обратное и называется обратимым тогда и только тогда, когда оно является взаимооднозначным или биекцией.

Примеры:

1. о тображение, обратное повороту вокруг центра С на угол +α, то есть поворот вокруг этого центра С на угол –α:

( )^-1=

2. Отображение, обратное центральной симметрии с центром С есть некая центральная симметрия с этим центром С:

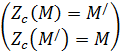⇒(Z_C)^-1=Z_C.

3. Найдем отображение f^-1, обратное отображению f, заданному формулами:

М^/=f(M): M=f^-1(M^/):

Обозначив координаты точки (х;у), а координаты ее образа (х^/,у^/), имеем:

f^-1:

§25. Группа преобразований.

Определение 1: преобразованием фигуры F называется ее взаимно однозначное отображение на себя.

Замечания:

1. По определению преобразование фигуры F – это такая биекция f, что f(F)=F (образом фигуры F является сама фигура F);

2. Согласно замечанию 3 из §24 для любого преобразования существует ему обратное преобразование и композиция любых двух преобразований ему некоторое преобразование;

3. В учебнике А.В. Погорелова (школьном и вузовском) под преобразованием понимается отображение фигуры не только на себя, но и на другие фигуры.

Примеры:

1. F – окружность, f – симметрия относительно диаметра АВ или центра О. В этом случае f(F)=F и f преобразование окружности в себя.

2. Пусть фигура F – вся плоскость. Тогда все отображения, рассмотренные ранее (параллельный перенос, осевая и центральная симметрии, поворот, тождественное преобразование) является преобразованиями плоскость.

Определение 2: множество G преобразований фигуры F называется группой, если выполняются следующие два условия:

1. композиция любых двух преобразований из G также является преобразованием. Принадлежащим G:

(f₁ G f₂ G) ⇒ (f₂° f₁ G);

2. преобразование, обратное любому преобразованию из G, есть также преобразование, принадлежащее G:

(f G) ⇒ (f^-1 G).

Теорема 2: группа G преобразований F содержит тождественное преобразований ε.

Доказательство.

Пусть f G – произвольное преобразование фигуры F. Тогда по условию 2) определения 2 имеем: f^-1 G, а по условию 1) определения 2 имеем: f^-1° f G. f^-1° f , значит, G.

Замечание: в теореме из §23 было доказано, что для композиции преобразований справедлив ассоциативный закон:

f₃°(f₂°f₁)= (f₃°f₂)°f₁.

Таким образом, определение 2 полностью согласовано с общим определением группы, известным из курса алгебры. (Непустое множество выполняются 4 аксиомы).

Определение 3: непустое множество G элементов произвольной природы называется группой, если выполняются следующие 4 аксиомы:

1. на множестве G определена бинарная операция (g₁, g₂) g₃;

2. эта операция ассоциативна: ((g₁, g₂), g₃)= (g₁, (g₂, g₃));

3. G обладает нейтральным элементом e: (g, е)=(е;g)=g;

4. Для каждого элемента g G существует обратный элемент g^-1:

(g, g^-1)=(g^-1;g)=e

для любых элементов g, g₁, g₂, g₃ множества G.

Определение 4: группа преобразований G₁ называется подгруппой группы преобразований G, если композиция преобразований из G₁ определена так же, как и в группе G.

Пример: параллельный перенос вдоль прямой l║J=О_х образуют группу, которая является подгруппой группы всех параллельных переносов плоскости.