§23. Векторное произведение векторов

Определение 1. Векторным произведением двух ненулевых неколлинеарных векторов называется вектор , такой что:

1. длина вектора равна произведению длин этих векторов на синус угла между ними:

2. вектор перпендикулярен этим векторам 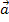и

3. векторы , образуют базис того же типа, что и векторы (правый базис).

Если же векторы коллинеарны или хотя бы один из них нулевой вектор, то их векторное произведение есть нулевой вектор

Обозначение: или

Теорема 1. (О геометрическом смысле векторного произведения). Длина векторного произведения двух ненулевых неколлинеарных векторов равна площади параллелограмма, построенного на этих векторах.

Доказательство.

Следствие. Площадь ∆ C выражается формулой:

Теорема доказана.

Теорема 2. Для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было нулевым вектором:

Доказательство.

Необходимость. Пусть , тогда согласно определению 1 либо , либо , либо , либо , либо . Во всех этих случаях вектора коллинеарны по определению.

Достаточность. Пусть , тогда снова по определению 1

Теорема доказана.

Следующие три теоремы сформулируем без доказательства.

Теорема 3. Векторное произведение антикоммутативно (антисимметрично):

Теорема 4. Векторное произведение ассоциативно относительно скалярного множителя:

Теорема 5. Векторное произведение дистрибутивно относительно суммы векторов:

Теорема 6.

Доказательство.

Доказательство следует из определения 1.

Пусть, например, , тогда имеем:

⟹ ⟹ .

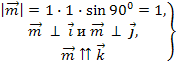Замечание. Достаточно запомнить первую формулу, вторая получается из первой, а третья – из второй с помощью круговой или циклической замены векторов

Теорема 7. (О координатах векторного произведения). Если в прямоугольном базисе (ортогональном) ( и , то

Доказательство.

Воспользуемся определением координат вектора и теоремами 3, 4, 5 и 6:

(см. определение определителя 3-его порядка)

Теорема доказана.

Пример. Вычислить площадь треугольника с вершинами А(-1,0,-1), В(0,2,-3), С(4,4,1).

Решение.

,

По следствию из теоремы 1 имеем: (кв.ед.).

§24. Смешанное произведение векторов

Определение 1. Смешанным произведением трёх векторов называется число, равное скалярному произведению векторного произведения векторов на вектор .

Обозначение. (

Можно показать, что

Теорема 1. Абсолютная величина (модуль) смешанного произведения трёх неколлинеарных векторов равна объёму параллелепипеда, построенного на этих векторах.

Доказательство.

Введём обозначения: , ∠(

Тогда имеем:

( (1)

По теореме 1 из §2 имеем:

(2)

Пусть - высота параллелепипеда ( .

Из ∆

Случай 1:

Случай 2:

В обоих случаях получаем:

. (3)

Подставляя значения (2) и (3) в формулу (1), окончательно получаем:

(

Итак,

. (4)

Теорема доказана.

Следствие 1.

. (5)

Доказательство следствия.

Следствие доказано.

Следствие 2. Знак смешанного произведения тройки некомпланарных векторов соответствует её ориентации, то есть если тройка правая, то , если тройка левая, то

Следствие 3. Три вектора коллинеарны тогда и только тогда, когда их смешанное произведение равно нулю.

Доказательство следствия.

Если тройка векторов коллинеарная, то объём параллелепипеда, построенного на векторах этой тройки, равно нулю. Обратно, если V_ПАР = 0, то вектора тройки коллинеарны.

Следствие доказано.

Замечание. Из трёх неколлинеарных векторов , можно составить шесть упорядоченных троек: причём первые три тройки векторов образуют правый базис, а последние три – левый базис (большой, указательный, средний пальцы).

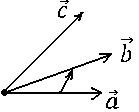
При перестановке любых двух векторов в каждой из первых троек получается копия – либо из трёх последних, поэтому в результате меняется ориентация упорядоченных троек векторов.

Если в упорядоченной тройке векторов осуществить циклическую перестановку векторов, то непосредственной проверкой убедимся, что при этом ориентация упорядоченной тройки векторов не меняется.

Из теоремы 1 следует, что при перестановке векторов в упорядоченной тройке модуль скалярного произведения не меняется, так как во всех случаях он равен объёму одного и того же параллелепипеда. Так же от скалярного произведения зависит ориентации тройки векторов.

Следствие 4.

(6)

Пример.

Используя формулу (6), то есть определение 1 дано корректно.

Теорема 2.

Теорема 3.

Доказательства теорем 2 и 3 следуют из свойств определителя 3-го порядка; мы их опускаем (см. теорему 4).

Теорема 4. Если в ортонормированном базисе

то

(7)

Доказательство. .

Теорема доказана.