§ 11. Взаимное расположение двух прямых
Определение.
Углом от прямой
до прямой
называется направленный
угол Θ(тэта), удовлетворяющий условиям:
при повороте на него прямая совмещается с прямой ;
.
Теорема
1.
Угол Θ от прямой
с уравнением
до прямой
с уравнением
выражается формулой:
(1)
Доказательство.
Пусть
,
,
то есть
,
.
Рассмотрим
два возможных случая взаимного
расположения прямых
,
и оси
.
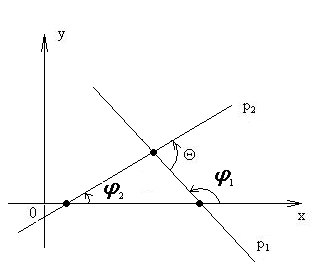
По теореме о внешнем угле треугольника имеем:
или
;
или
;
В обоих случаях получаем:
.
Теорема доказана.
Следствие 1. Условием параллельности двух прямых является следующее:
.
Доказательство.
.
Следствие 2. Условием перпендикулярности двух прямых является следующее:
.
Доказательство.
.
Пример.
Записать уравнение прямой, проходящей
через точку
перпендикулярно прямой с уравнением
.
Решение:
Будем искать уравнение искомой прямой в виде . Имеем: .
Найдем угловой коэффициент данной прямой:
.
Найдем угловой коэффициент искомой прямой:
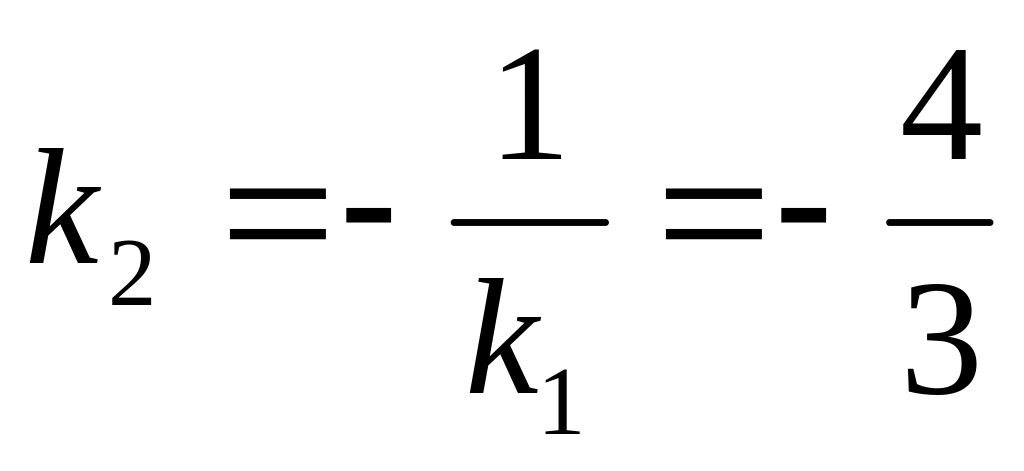.Записываем уравнение искомой прямой:
.
Теорема
2.
Угол
от прямой
с
уравнением
(2)
и
прямой
с
уравнением
(3)
выражается формулой:
(4)
Доказательство.
Запишем уравнения данных прямых (общие) в виде уравнений с угловым коэффициентами:
,
,
.
,
,
.
Подставим
значения
и
в формулу (1):
.
Теорема доказана.
Замечание
1. Формула
(4)
может
использоваться и в случае
(прямые
и
параллельны оси
и
).
Следствие 1. Условием параллельности двух прямых является следующее:
.
Замечание
2.
Если выполняются соотношения
,
то уравнения (2)
и (3)
эквивалентны, а прямые
и
совпадают (параллельны в широком смысле).
Если же
,
то система из уравнений (2)
и (3)
несовместна, а прямые
и
не имеют общих точек (параллельны в
узком смысле).
Следствие 2. Условием перпендикулярности двух прямых является следующее:
. 
Замечание
3.
Условия параллельности и перпендикулярности
двух прямых могут быть выведены и иначе.
Пусть
и
- нормальные векторы данных прямых.
Тогда имеем:
1)
для параллельных прямых
и
векторы
и
коллинеарны, тогда
или
,
.
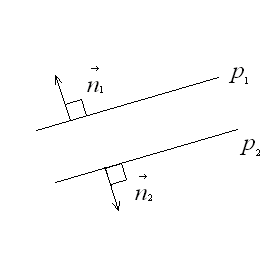
2)
для перпендикулярных прямых
и
векторы
и
ортогональны, тогда
или
,
.
Пример.
Найти угол между медианой CD
и стороной AB
треугольника с вершинами:
,
,
.
Решение.
1)
Уравнение медианы CD
данного треугольника ABC
уже было найдено ранее:
(смотри
пример из §7).
Для этого сначала нашли точку D как середину отрезка AB.
Затем составили уравнение прямой CD как прямой, проходящей через две данные точки C и D.
2) Составляем аналогично уравнение прямой AB:
или
или
.
3) угол между прямыми CD и AB:
1 способ:
.
2 способ:
§ 12. Нормальное уравнение прямой. Полярное уравнение прямой. Пучок прямых
10.
Определение
1.
Уравнение прямой
называется нормальным
уравнением
этой прямой, если
(то есть нормальный вектор
является единичным (ортом)).
Очевидно, любое общее уравнение прямой можно привести к нормальному (нормальной форме).
Для
этого обе части общего уравнения надо
умножить на некоторое число
:
и выбрать
так, чтобы вектор
был единичным, отсюда
.
Число называется нормирующим множителем.
Легко
видеть, что
,
так как
.
Пусть
прямая
задана нормальным уравнением:
,
где
<
0,
.
(Этого всегда можно добиться, умножив
обе части уравнения прямой на -1). Начало
координат
лежит в отрицательной полуплоскости
от прямой
.
Значит,
,
где
основание перпендикуляра, опущенного
из начала координат на прямую
.
Поэтому
,
тогда
,
- расстояние от начала координат до
прямой
.
Тогда имеем уравнение:
,
где 
. (1)
Определение
2.
Угол
называется полярным углом нормали
данной прямой.
Теорема. При подстановке в левую часть уравнения (1) координат любой точки плоскости получается число, равное с точностью до знака расстоянию этой точки до прямой .
Доказательство.
Пусть
- произвольная точка данной прямой
,
тогда
. (2)
и уравнение прямой можно представить в виде:
. (3)
Для этого достаточно вычесть из уравнения (1) уравнение (2).
Пусть
теперь
- произвольная точка плоскости, не
принадлежащая прямой
.
Подставим ее координаты в левую часть
уравнения (3):
.
(4)
где
- нормальный вектор прямой
.
Обозначим
.
Тогда получаем:
.
Таким
образом, действительно, при подстановке
координат точки
в левую часть уравнения (1) получается
с точностью до знака расстояние
точки
до прямой
.
Теорема доказана.
Замечание.
Знак выражения
зависит от того, как направлены векторы
и
(в одну полуплоскость, или в разные).
Поэтому для точек одной полуплоскости
это скалярное произведение положительно,
а для другой – отрицательно.
20.
Выведем полярное уравнение прямой, не
проходящей через полюс, заданной в
системе координат
нормальным уравнением
… (1).
Для
этого воспользуемся формулами
преобразования полярных координат в
декартовы:
Подставив значения и в нормальное уравнение прямой, получим:
.
Отсюда получаем полярное уравнение данной прямой:
.
(5)
Если
же прямая проходит через полюс, то её
задают уравнения
и
.
Замечание
2.
В уравнении (5)
и
являются полярными координатами
произвольной точки
прямой
,
- расстояние прямой от полюса,
полярный угол нормали.
,
.
30.
Определение
3.
Пучком прямых с центром
называется совокупность прямых плоскости,
проходящих через точку А.
Пусть даны уравнения двух прямых пучка:
. (1)
. (2)
где
.
Рассмотрим уравнение:
.
(3)
где
и
могут принимать любые значения,
одновременно не равные нулю. Это уравнение
линейное, а значит, является уравнением
некоторой прямой. Координаты точки
пересечения данных прямых удовлетворяют
уравнению (3), так как обе данные прямые
проходят через центр
пучка, то есть координаты точки
удовлетворяют уравнениям (1) и (2).
Более того, оказывается, что числа и всегда можно подобрать так, чтобы уравнение (3) определяло бы любую (заранее назначенную) прямую пучка с центром . Поэтому уравнение (3) называется уравнением пучка прямых с центром .
Например,
при
,
получается прямая с уравнением (1), а при
,
- прямая с уравнением (2).
Если
положить
,
,
то получим уравнение:
.
(4)
Этим уравнением можно определить любую прямую пучка с центром А, кроме прямой (2).
Пример. Даны уравнения сторон треугольника ABC:
AB:
;
AC:
;
BC: .
Найти уравнение высоты AD (прямой, на которой лежит эта высота).
Решение.
1 способ.
1)
Рассмотрим пучок прямых с центром
,
затем уравнение прямой AD
этого пучка (искомой прямой - высоты) в
виде (4):
или
(5).
2)
Находим значение
из условия перпендикулярности прямых
AD
и BC:
.
3)
Уравнение высоты AD
имеет вид:
или
.
2 способ.
1)
Находим точку
:
.
2) Далее поступаем, как и в примере из §12 перед теоремой 2.