§6. Геометрический смысл уравнений и неравенств в координатах

1⁰. Напомним, что фигурой называется любое множество точек. Рассмотрим фигуру Φ, расположенную на плоскости с заданной на ней аффинной системой координат .

Определение 1. Условием, определяющим фигуру Φ в данной системе координат, называется уравнение, неравенство или система, которым:

1. удовлетворяют координаты любой точки этой фигуры,

2. и не удовлетворяют координаты любой точки, не принадлежащей этой фигуре.

Уравнение, определяющее фигуру Φ, называется уравнением фигуры Φ в данной системе координат.

Координаты в этих уравнениях или неравенствах могут принимать всевозможные значения (точнее, различные значения), поэтому они называются текущими координатами точки фигуры Φ.

Замечания.

1) Метод координат в геометрии состоит в том, что посредством координат точек геометрические объекты или фигуры задают аналитически с помощью чисел, уравнений, неравенств и их систем. Тем самым при доказательстве теорем или решении геометрических задач используют аналитические методы. Это существенно упрощает рассуждения и часто позволяет доказывать теоремы и решать задачи алгоритмически, то есть, производя последовательные или иные вычисления;

2) При изучении геометрических объектов методом координат основными являются 2 задачи:

а) по заданным геометрическим свойствам фигуры составить определяющие ее аналитические условия;

в) по заданным аналитическим условиям, определяющим фигуру, выяснить ее геометрические свойства.

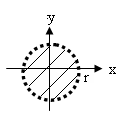
Пример 1. Составим уравнение окружности (омега) радиуса r с центром в начале

прямоугольной декартовой системы координат .

Пусть х и у – некоторые координаты произвольной точки М и плоскости Оху.

1) М . (1)

Координаты любой точки М окружности удовлетворяю уравнению (1)

2) М₁ не принадлежит или .

Таким образом, координаты любой точки М₁, не принадлежащей окружности , не удовлетворяют уравнению (1). Согласно определению 1 уравнение (1) является уравнением окружности в системе координат .

Легко видно, что в соответствующей полярной системе координат уравнение окружности имеет вид: ρ=r, при этом 0⁰≤Ө≤360⁰.

Замечания.

3) Круг, ограниченный этой окружностью, определяется неравенством:

4) Внутренняя область этого круга определяется строгим неравенством: ;

5) Внешняя область этого круга определяется неравенством:

Пример 2. По уравнению в полярных координатах построим линию, называемую кардиоидой (кардио - сердце).

М(ρ, Ө): ρ=α(1+cos Ө)

Ө	00	900	1800	2700	3600
ρ	2а	а	0	а	2а

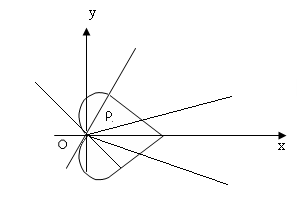
Составим уравнение кардиоиды в прямоугольных декартовых координатах.

Имеем: cosӨ=

При возведении в квадрат обеих частей уравнения здесь не получается посторонних решений (линия симметрична относительно оси Ох).

2⁰. Пусть фигура Φ₁ задана уравнением: Ғ₁(х,у)=0, а фигура Φ₂ – уравнением: Ғ₂(х,у)=0

Тогда:

1) объединение этих фигур Φ₁ и Φ₂ задается уравнением Ғ₁(х,у) Ғ₂(х,у)=0

2) пересечение этих фигур задается системой уравнений:

Примеры.

1) х=0 – уравнение оси ординат Оу, у=0 – уравнение оси абсцисс Ox.

2) х у=0 – уравнение пары прямых Ох и Оу.

3) - система уравнений, определяющая точку – начало координат О(0;0)

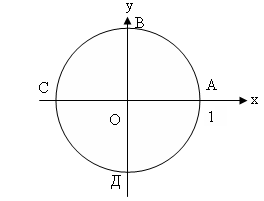
4) – система уравнений, определяющая четверку точек А(1,0), В(0,1), С(-1,0), Д(0,-1).

Определение 2. Линия на плоскости называется алгебраической, если в какой-либо аффинной системе координат (в частности, в прямоугольной декартовой ) уравнение этой линии можно представить в виде: Ғ(х,у)=0, где Ғ(х,у) – многочлен от переменных х, у, то есть сумма одночленов вида (а R, s, t Z). Степенью члена при а ≠0 называется число s+t . Степенью многочлена Ғ(х,у) называется наивысшая степень его членов. Степень многочлена Ғ(х,у) называется порядком данной линии.

Примеры.

1) или – прямая линия – алгебраическая линия 1-го порядка.

2) х²+у²=1 или х²+у²-1=0 – окружность – алгебраическая линия 2-го порядка.

3) (х²+у²-ах)²=а²(х²+у²) или (х²+у²-ах)²-а²(х²+у²)=0 – кардиоида – алгебраическая линия 4-го порядка.

4) – не является алгебраической линией (таких линий существует бесконечное множество, еще, например, y=e ͯ они называются трансцендентными (выходящими за пределы).

Замечание 1. Можно доказать следующую теорему: понятия алгебраической линии и ее порядка не зависят от выбора аффинной системы координат.

Определение 3. Аналитической геометрией на плоскости называется раздел геометрии, в котором свойства алгебраических линий второго и первого порядков исследуются алгебраическими методами.

Замечания.

2) Одним из основателей аналитической геометрии (наряду с Пьером Ферма) является Рене Декарт – французский философ, математик, физик, физиолог;

3) В дальнейшем будем использовать только прямоугольную декартову систему координат.