§39. Цилиндрические поверхности

Определение. Поверхность, обладающая тем свойством, что вместе с каждой своей точкой М она содержит всю прямую, проходящую через М и параллельную данному ненулевому вектору называется цилиндрической поверхностью или цилиндром. Прямые, параллельные вектору и принадлежащие цилиндрической поверхности, называются образующими этой поверхности.

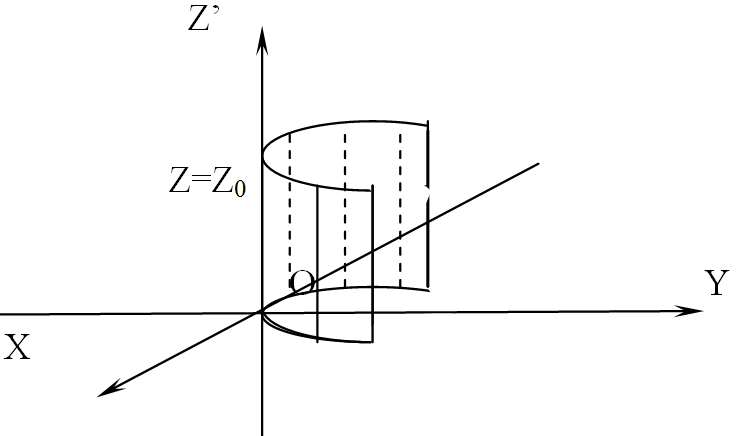
Пусть γ – некоторая линия (не обязательно плоская), а - ненулевой вектор. Согласно определению поверхность, образованная всеми прямыми, каждая из которых проходит через точку линии γ параллельно вектору , является цилиндрической. В этом случае линия γ называется направляющей этой поверхности.

Докажем следующую теорему.

Теорема. Пусть в пространстве дана прямоугольная декартовая система координат O и в плоскости Oxy в системе координат O задана линия γ уравнением

F(x,y)=0. (1)

Тогда уравнение (1) определяет в пространстве цилиндрическую поверхность ξ с направляющей линией γ и образующими, параллельными оси OZ (то есть вектору ).

Доказательство.

Возьмем произвольную точку M₀ (x₀; y₀; z₀) пространства и рассмотрим прямую m, проходящую через эту точку, и направляющий вектор . Эта прямая m пересекает плоскость Oxy в некоторой точке M₁ (x₀; y₀; 0). Эта же точка M₁ на плоскости Oxy в системе координат O имеет координаты (x₀; y₀).

Если М₀ – точка поверхности ξ, то прямая M₀M₁ является образующей поверхности ξ, поэтому точка M₁ лежит на кривой γ. То есть ее координаты (x₀; y₀) удовлетворяют уравнению (1) линии γ: F(x₀,y₀)=0. Полученное равенство означает, что и координаты x₀; y₀; z₀ точки M₀ также удовлетворяют уравнению (1).

Если же точка M₀ не принадлежит поверхности ξ, то и точка M₁ не лежит на кривой γ, поэтому ее координаты (x₀; y₀) не удовлетворяют уравнению линии γ: F(x₀,y₀)≠0. Полученное неравенство означает, что и координаты точки M₀ не удовлетворяют уравнению (1).

Итак, уравнение (1) есть уравнение цилиндрической поверхности с направляющей линией γ и параллельными оси OZ образующими (если О принадлежит γ, то ось OZ служит одной из образующих).

Замечания.

1) если уравнение G(x, z)=0 в плоскости Oxz в системе координат O определяет линию γ', то это же уравнение в пространстве определяет цилиндр с направляющей γ' и параллельными оси OY образующими;

2) если уравнение (1) есть уравнение второй степени относительно X и Y, то есть γ- линия второго порядка, то цилиндрическая поверхность с направляющей γ и параллельными вектору образующими является цилиндром второго порядка. Вид его определяется видом направляющей линии γ.

Рассмотрим цилиндрические поверхности 2-го порядка.

1. Эллиптический цилиндр

.

Все образующие этого цилиндра параллельны оси OZ, все его сечения плоскостями, параллельными плоскости Oxy есть равные между собой эллипсы. Любой из них, например, сечение плоскостью Oxy можно принять за направляющую.

При a=b эти сечения являются окружностями, цилиндр является поверхностью вращения и называется круговым цилиндром.

Он образован вращением прямой с уравнением , лежащей в Oxz, вокруг оси OZ: x²+y²=a².

2. Гиперболический цилиндр

.

Все образующие этого цилиндра параллельны оси OZ, направляющей может служить, например, гипербола, лежащая в плоскости Oxy.

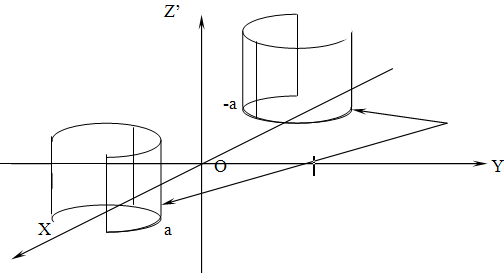
3. Параболический цилиндр

.

Все образующие этого цилиндра параллельны оси OZ, направляющей может служить, например, парабола x²=2a²y, лежащая в плоскости Oxy (z=0).

4. – цилиндр, распавшийся на пару плоскостей , пересекающихся по оси OZ.

5. – цилиндр, распавшийся на пару плоскостей , параллельных плоскости OXY.

6. – цилиндр, состоящий из пары совпадающих с плоскостью OYZ плоскостей.