VII. Поверхности второго порядка

§33. Общее уравнение поверхности второго порядка

Определение. Алгебраической поверхностью n-го порядка называется множество точек пространства, имеющее в некоторой аффинной системе координат , в частности, в прямоугольной декартовой системе координат , уравнение вида:

, где - многочлен n-ой степени относительно с действительными коэффициентами.

Можно доказать, что определение поверхности n-го порядка не зависит от выбора системы координат в пространстве, то есть если в какой либо АСК поверхность задаётся уравнением n-ой степени, то и в любой другой АСК она также задаётся уравнением n-ой степени.

Примеры.

1. Алгебраической поверхностью первого порядка является любая плоскость с общим уравнением , где ;

2. Алгебраическая поверхность второго порядка имеет уравнение вида: , где хотя бы один из коэффициентов членов второй степени отличен от нуля.

Это уравнение называется общим уравнением поверхности 2-го порядка.

Так же, как и для линии второго порядка на плоскости, можно доказать, что уравнение любой поверхности 2-го порядка с помощью надлежащего выбора системы координат (прямоугольной декартовой) может быть приведено к одному из 17 (семнадцати) простейших видов, которые называются каноническими.

Общую теорию поверхностей второго порядка мы изучать не будем, исследуем свойства этих поверхностей по их каноническим уравнениям.

I. Эллипсоиды

1. Эллипсоид: .

2. Мнимый эллипсоид (пустое множество точек): .

II. Гиперболоиды

3. Однополостный гиперболоид: .

4. Двуполостный гиперболоид: .

III. Параболоиды

5. Эллиптический параболоид: .

6. Гиперболический параболоид: .

IV. Конусы

7. Конус: .

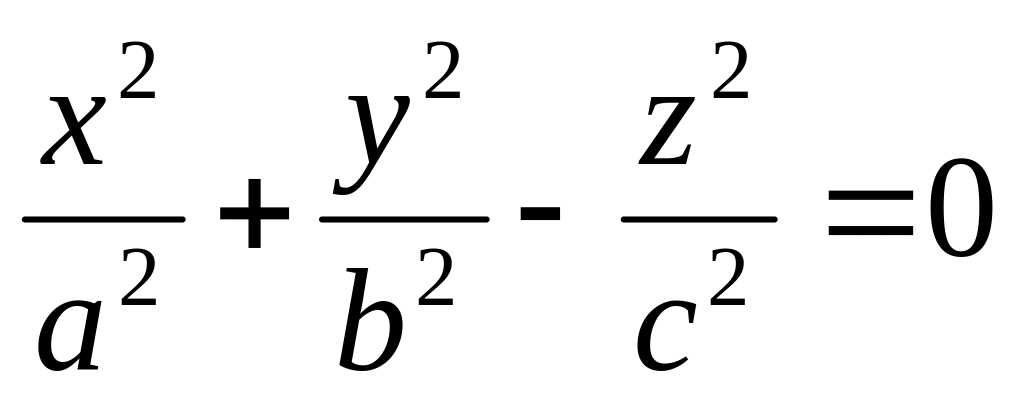8. Мнимый конус (точка O(0,0,0)): .

V. Цилиндры

9. Эллиптический цилиндр: .

10. Гиперболический цилиндр: .

11. Параболический цилиндр: .

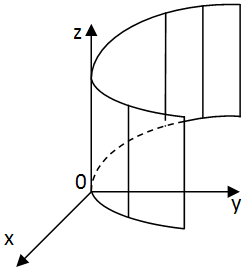
12. Мнимый цилиндр (пустое множество точек):

VI. Пары плоскостей

13. Пара пересекающихся плоскостей:

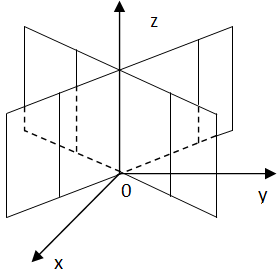
14. Пара мнимых плоскостей, пересекающихся по действительной прямой:

15. Пара различных параллельных плоскостей:

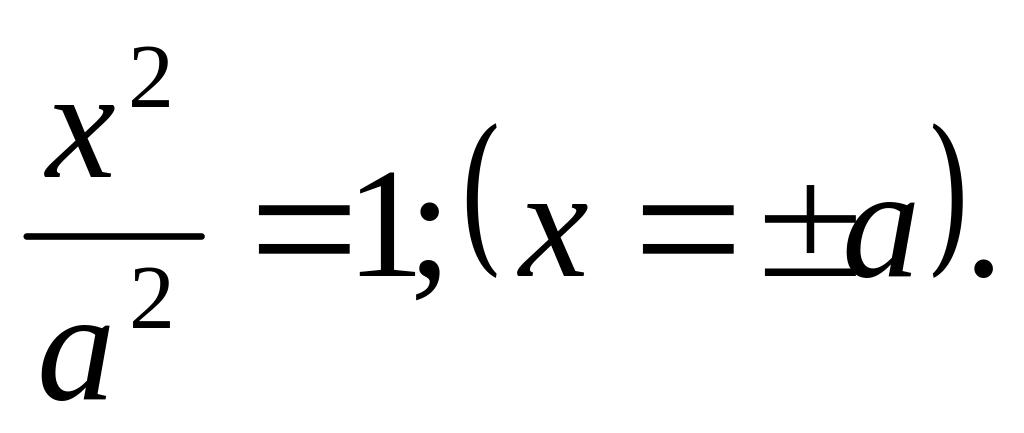
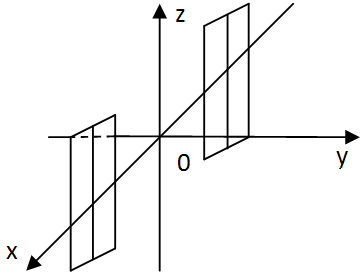
16. Пара совпавших плоскостей:

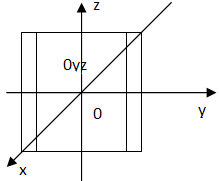
17. Пара мнимых параллельных плоскостей (пустое множество точек). (Изображения поверхностей 2-го порядка смотреть в учебнике геометрии часть I, глава IX.)

§34. Эллипсоид

Эллипсоид задаётся своим каноническим уравнением:

. (1)

1. Плоскости, оси и центр симметрии

а) Так как переменная z содержится в уравнении (1) лишь во второй степени, то это уравнение не изменится при замене на .

Следовательно, если точка принадлежит эллипсоиду, то ему также принадлежит и точка .

Э ти точки симметричны относительно плоскости , значит и весь эллипсоид симметричен относительно этой плоскости.

Аналогично, эллипсоид симметричен и относительно плоскостей и .

б) Так как уравнение (1) не изменяется при одновременной замене на и на , то эллипсоид симметричен относительно оси .

Аналогично, эллипсоид симметричен и относительно осей и .

в) Так как уравнение (1) не изменится при одновременной замене на , на на , то эллипсоид симметричен относительно начала координат.

Определение 1. Центр симметрии поверхности второго порядка называется её центром, а её оси симметрии – осями поверхности второго порядка.

Таким образом, эллипсоид с уравнением (1) имеет:

• один центр симметрии – начало координат;

• три оси симметрии – оси , , и ;

• три плоскости симметрии – плоскости , , .

2. Вершины

Определение 2. Вершинами поверхности 2-го порядка называются точки пересечения её с осями.

Найдём вершины эллипсоида с уравнением (1).

или , отсюда .

Точки пересечения эллипсоида с осью обозначим:

и .

Аналогично получим точки пересечения эллипсоида с осью :

и .

И осью :

и .

Итак, эллипсоид имеет шесть вершин. Числа называются комре эллипсоида.

3. Главные сечения

Определение 3. Множество точек (кривая линия), получающиеся при пересечении некоторой поверхности (не обязательно 2-го порядка) плоскостью, называется сечением этой поверхности.

Определение 4. Сечения поверхности 2-го порядка её плоскостями симметрии называются её главными сечениями.

Легко видеть, что все главные сечения эллипсоида есть эллипсы:

Сечение плоскостью :

Сечение плоскостью :

Сечение плоскостью :

4. Сечения плоскостями, параллельными плоскостям симметрии

Рассмотрим сечение эллипсоида с уравнением (1) плоскостью α, параллельной плоскости Оху:

(2)

В зависимости от величины h возможны случаи:

1. и плоскости α с уравнением z=h эллипсоид не пересекает.

2. и сечением является либо точка C1(0;0;c), либо точка C2(0;0;-c), то есть, одна из вершин – эллипсоида.

3. и получаем систему уравнений:

(3)

В уравнении (3) положив: , приходим к уравнению эллипса с полуосями а₁ и b₁:

. (4)

Итак, в этом случае в сечении мы получаем эллипс, центр которого лежит на оси Oz в точке D(0;0;h). Легко видеть, что при уменьшении полуоси а₁ и b₁ возрастают и при h=0 имеем: a₁=a, b₁=b – сечение является главным.

Аналогично можно показать, что сечение эллипсоида с уравнением (1) плоскостями x=h или y=h является либо эллипсом, либо точкой – соответствующей вершиной эллипсоида, либо пустым множеством.

Заметим дополнительно, что из уравнения (1) следует, что

Поэтому имеем: -a ≤ x ≤ a, -b ≤ y ≤b, -c ≤ z ≤ c. Отсюда следует, что все точки эллипсоида (кроме его вершин) лежат внутри прямоугольного параллелепипеда с измерениями 2a, 2b, 2c. Грани его параллельны координатным плоскостям, а вершины эллипсоида служат центрами симметрии этих граней.

Изобразим теперь эллипсоид, используя проведённые выше исследования его формы.

5. Виды эллипсоидов

1. Если все полуоси эллипсоида различны: a≠b≠c, то он называется трёхосным.

2. Если две полуоси эллипсоида равны, например, a=b, то он является поверхностью вращения. Все его сечения, перпендикулярные оси вращения Oz, есть окружности. Эллипсоид называется в этом случае эллипсоидом вращения с осью вращения Oz и имеем каноническое уравнение:

. (5)

3. Если все три оси эллипсоида равны: a=b=c, то он представляет собой сферу с центром в начале координат радиуса r = a:

. (6)

Следовательно, сфера является частным случаем эллипсоида.

Можно показать, что любой трёхосный эллипсоид с уравнением (1) можно получить из некоторой сферы, например, с уравнением (6), с помощью последовательного сжатия к двум взаимно перпендикулярным плоскостям симметрии этой сферы.

Замечание. Эллипсоид с центром O’(x₀;y₀;z₀) и полуосями a, b, c, параллельными осям координат, имеем уравнение: =1.

В частности, сфера радиуса r = a с центром в точке O’(x₀;y₀;z₀) имеем уравнение: +