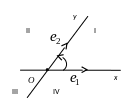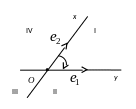- •I. Метод координат на плоскости
- •§ 1. Аффинная система координат
- •§ 2. Деление отрезка в данном отношении
- •§ 3. Переход к новой аффинной системе координат
- •§ 4. Прямоугольная декартова система координат
- •1) При системах координат одинаковых типов:
- •2.) При системах координат различных типов:
- •§5. Полярная система координат
- •§6. Геометрический смысл уравнений и неравенств в координатах
- •II. Прямая линия на плоскости
- •§7. Уравнения прямой, проходящей через данную точку и через две данные точки
- •§8. Общее уравнение прямой
- •§9. Другие способы задания прямой
- •10. Параметрические уравнения прямой
- •20. Уравнение прямой в отрезках на осях координат
- •30. Уравнение прямой с угловым коэффициентом
- •§10. Взаимное расположение точки и прямой
- •§ 11. Взаимное расположение двух прямых
- •Будем искать уравнение искомой прямой в виде . Имеем: .
- •§ 12. Нормальное уравнение прямой. Полярное уравнение прямой. Пучок прямых
- •III. Линии второго порядка
- •§13. Эллипс («Недостаток»)
- •§14. Директрисы эллипса
- •§15. Исследование уравнения эллипса
- •1. Оси и центры
- •2. Вершины
- •3. Расположение относительно осей
- •4. Другие уравнения эллипса
- •§16. Гипербола («Избыток» - греческий)
- •§17. Исследование уравнения гиперболы
- •1. Оси и центр
- •2. Вершины
- •3. Расположение относительно осей
- •4. Асимптоты ( от греческого – несовпадающий, не касающийся)
- •§18. Парабола (“приложение”)
- •§19. Исследование уравнения параболы
- •1. Ось и вершина
- •2. Расположение относительно оси и директрисы
- •3. Фокальная хорда
- •4. Другие виды уравнения параболы
- •§20. Уравнения эллипса, гиперболы и параболы в полярных координатах
- •§21. Общее уравнение линии второго порядка
- •IV Преобразование плоскости
- •§21. Понятие отображения.
- •§22. Отображения фигур на плоскости.
- •§23. Композиция отображений.
- •§24.Обратное отображение.
- •§25. Группа преобразований.
- •§26. Группа движений.
- •Классификация движений плоскости:
- •§27. Формулы движений.
- •§28. Группа симметрий фигуры.
- •§29. Группа преобразований подобия.
- •§30. Формулы подобия.
- •§31. Группа аффинных преобразований.
- •§32. Применение преобразований плоскости к решению задач.
- •V. Метод координат в пространстве
- •§22. Аффинная и прямоугольная декартова системы координат в пространстве
- •§23. Векторное произведение векторов
- •§24. Смешанное произведение векторов
- •VI. Плоскости и прямые
- •§ 1. Общее уравнение плоскости
- •§26. Специальные виды уравнений плоскости
- •§27. Расстояние от точки до плоскости
- •§ 28. Взаимное расположение двух плоскостей
- •§ 29. Связка плоскостей и пучок плоскостей
- •§ 30. Способы задания прямой в пространстве
- •10. Параметрические уравнения прямой
- •20. Канонические уравнения прямой
- •30. Связка прямых
- •40. Уравнения прямой, проходящей через две точки
- •50. Общие уравнения прямой
- •§31. Взаимное расположение двух прямых в пространстве
- •§ 32. Взаимное расположение прямой и плоскости
- •VII. Поверхности второго порядка
- •§33. Общее уравнение поверхности второго порядка
- •§34. Эллипсоид
- •§35. Однополостный гиперболоид
- •§36. Двуполостный гиперболоид
- •§37. Эллиптический параболоид
- •§38. Гиперболический параболоид
- •§39. Цилиндрические поверхности
- •§40. Конические поверхности
- •§41. Прямолинейные образующие поверхностей второго порядка.
- •10. Однополосный гиперболоид.
- •20. Гиперболический параболоид.
I. Метод координат на плоскости
§ 1. Аффинная система координат
Определение
1.
Аффинной
системой координат
или аффинным
репером
называется совокупность некоторой
точки О
и некоторого базиса (![]() ,
,![]() ).
(аффинное = родственное, репер = метка).
).
(аффинное = родственное, репер = метка).
Точка
О
называется началом
координат,
![]() и
- координатными
векторами.
и
- координатными
векторами.
Если базис ( , ) – правый, то аффинная система координат называется правой, если базис левый, то – левой.
Определение 2. Осью называется прямая с выбранным на ней направлением, началом отсчета и единичным отрезком. Две оси, проходящие через начало координат и имеющие направления векторов и , называются соответственно осью абсцисс и осью ординат или координатными осями.
Четыре части, на которые они делят плоскость, называются координатными углами или квадрантами.
Обозначения:
ось абсцисс –
![]() ,
,
![]() ;
;
ось
ординат –
![]() ,
,
![]() ;
;
система
координат -
![]() ,
,
![]() .
.
Правая система координат
|
Левая система координат
|
Определение
3.
Радиус-вектором
точки М
плоскости называется вектор
![]() .
Его координаты x
и y
в базисе (
,
)
называются координатами
точки М
в аффинной системе координат, при этом
х
называется абсциссой,
у
– ординатой.
.
Его координаты x
и y
в базисе (
,
)
называются координатами
точки М
в аффинной системе координат, при этом
х
называется абсциссой,
у
– ординатой.
Обозначение:
![]() ,
,
![]() ,
,
![]() .
.
По
определению:
![]()
![]() .
.
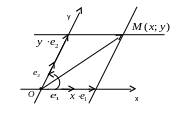
Определение 4. Плоскость называется ориентированной, если на ней выбрана какого-либо вида аффинная система координат – правая или левая и, следовательно, определено направление отсчета углов (против или по часовой стрелке). Система координат выбранного вида называется положительно ориентированной, а выбранное направление отсчета углов – положительным.
Замечание. Будем считать плоскость положительно ориентированной, на ней выбрана правая система координат и, следовательно, положительным направлением отсчета углов – против часовой стрелки.
§ 2. Деление отрезка в данном отношении
Определение.
Пусть на прямой лежат направленный
отрезок
![]() и произвольная точка М.
Отношением,
в котором эта точка делит данный отрезок,
называется такое число λ, что:
и произвольная точка М.
Отношением,
в котором эта точка делит данный отрезок,
называется такое число λ, что:
![]() (1)
(1)
Обозначение: λ=(AB,M)
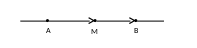
ЧАСТНЫЕ СЛУЧАИ:
1)
λ>0
![]()
![]() ,
точка М
лежит внутри
отрезка АВ,
,
точка М
лежит внутри
отрезка АВ,
![]() .
.
λ=1
![]() ,
М
– середина
отрезка
АВ.
,
М
– середина
отрезка
АВ.
2)
λ=0
![]() ,
,
![]() - точка М
совпадает с началом А
отрезка АВ.
- точка М
совпадает с началом А
отрезка АВ.
3)
λ<0
![]() ,
точка М
лежит вне
отрезка АВ,
,
точка М
лежит вне
отрезка АВ,
![]() .
.
Замечание:
λ![]() -1
, т. к. в этом случае
-1
, т. к. в этом случае
![]() или
или
![]() и
и
![]() и
и
![]() ,
то есть
,
то есть
![]() .
.
Теорема. Если точка M(x;y) делит в отношении λ -1 направленный отрезок с началом А(х1;у1) и концом В(х2;у2), то
![]() ,
,
![]() .
(2)
.
(2)
Доказательство.
- согласно определению. Перейдем к
координатам:
![]() ,
,
![]() .
.
Из
условия равенства векторов
![]() и
и
![]() имеем:
имеем:
![]()
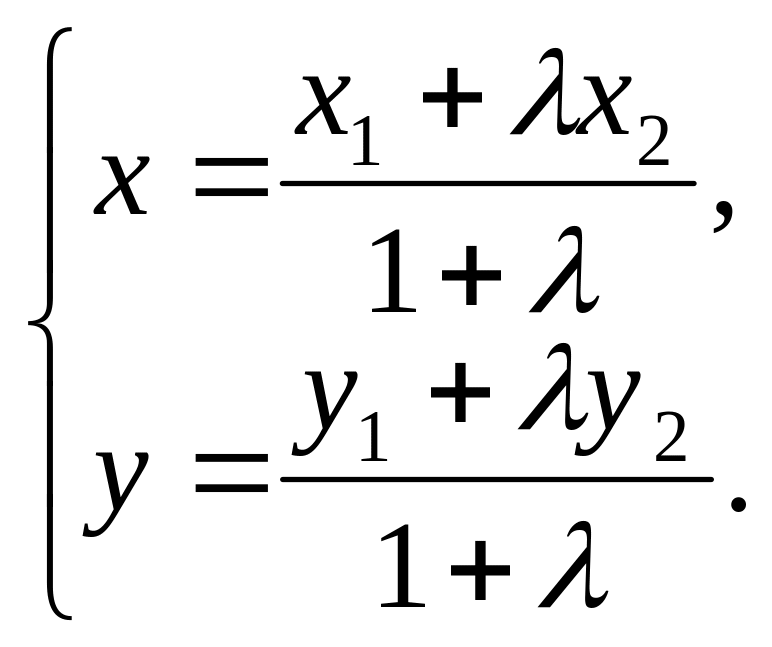
Теорема доказана.
Следствие.
Если М
– середина направленного отрезка
![]() ,
то λ=1 и
,
то λ=1 и
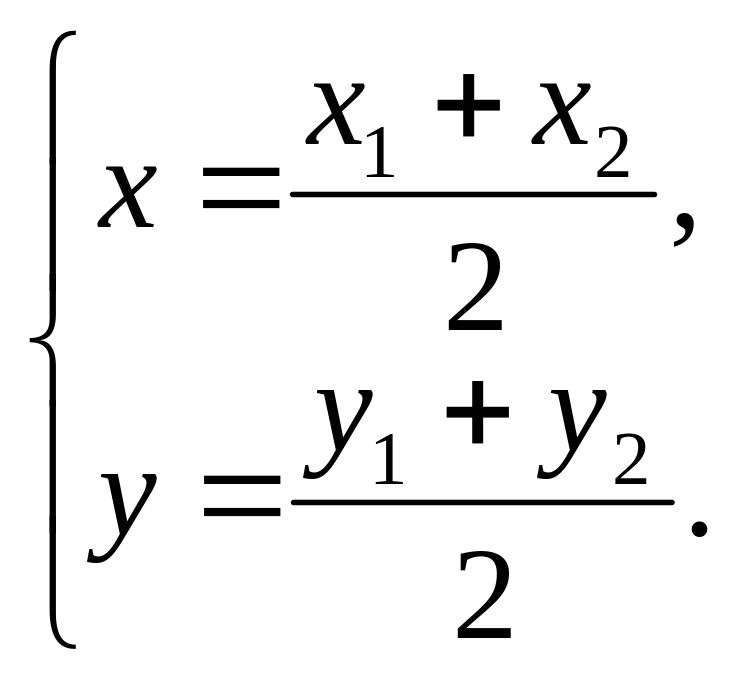 (3)
(3)
§ 3. Переход к новой аффинной системе координат
Рассмотрим
две аффинные системы координат. Одну
из них обозначим
и назовем старой,
другую обозначим
![]() и назовем ее новой.
и назовем ее новой.
Теорема.
Пусть 1) начало координат и координатные
векторы новой системы имеют в старой
системе координаты:
![]() ,
,
![]() ,
,
![]() ;
2) произвольная точка М
имеет в старой системе координаты x,
y,
а в новой системе координаты
;
2) произвольная точка М
имеет в старой системе координаты x,
y,
а в новой системе координаты
![]() .
Тогда имеют место формулы:
.
Тогда имеют место формулы:
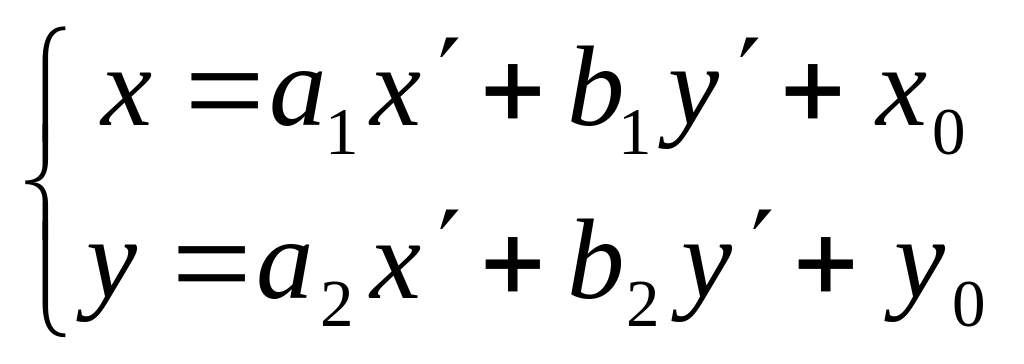 ,
где
,
где
![]() . (*)
. (*)
Доказательство.
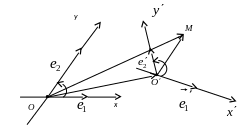
СТАРАЯ СИСТЕМА НОВАЯ СИСТЕМА
КООРДИНАТ КООРДИНАТ
По определению координат точек и векторов имеем для старой системы координат :
![]() ;
(1)
;
(1)
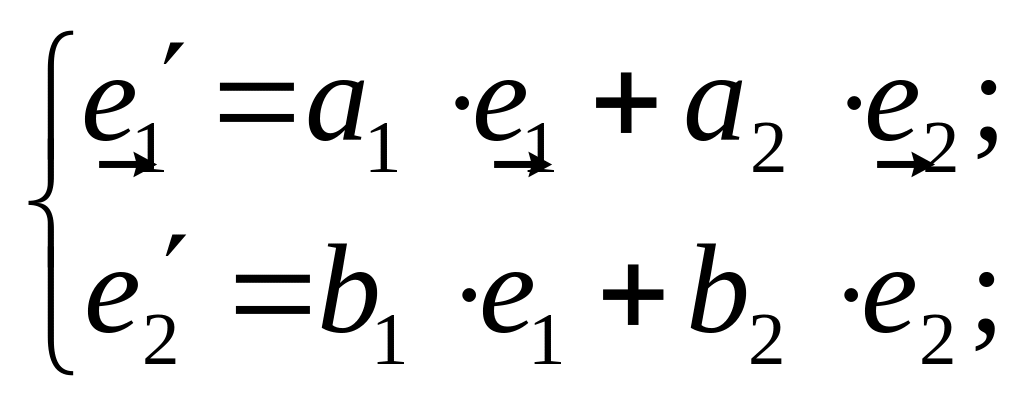 (2)
(2)
. (3)
Для новой системы координат аналогично имеем:
![]() .
(4)
.
(4)
Подставим
выражения
![]() и
и
![]() из (2) в (4):
из (2) в (4):
![]() .
(5)
.
(5)
По правилу треугольника имеем:
![]() .
(6)
.
(6)
Подставим в это равенство выражения (3), (1) и (5):
![]()
![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() .
.
Приведем подобные члены:
![]()
![]() +
+![]()
![]() =
=![]() +
+![]() .
.
Так как координаты вектора в данном базисе определены однозначно, то формулы (*) справедливы:
 (*)
(*)
Теорема доказана.
Замечания.
1)
в правой части равенств (*) коэффициентами
при
![]() служат координаты
служат координаты
![]() и
и
![]() вектора
в старой системе координат, коэффициентами
при
вектора
в старой системе координат, коэффициентами
при
![]() - координаты
- координаты
![]() и
и
![]() вектора
в старой системе координат, свободными
членами – координаты нового начала
в старой системе координат;
вектора
в старой системе координат, свободными
членами – координаты нового начала
в старой системе координат;
2) по определению базиса векторы и неколлинеарны, а по теореме из §3: определитель из их координат отличен от нуля:
.
Можно
доказать, что если старая и новая системы
координат одного
типа
(например, обе правые), то
![]() ,
если же разных
типов,
то
,
если же разных
типов,
то
![]() .
.